In sage, using the trick of differentiating from the answer by @stevengregory:
var("a,b,d,e,f,A,B,C,D,S1,S2")
eq1=(a*A+b*B)^2+d*A+e*B+f==0
eq2=(a*C+b*D)^2+d*C+e*D+f==0
eq3=2*(a*A+b*B)*(a+b*S1)+d+e*S1==0
eq4=2*(a*C+b*D)*(a+b*S2)+d+e*S2==0
solve([eq1,eq2,eq3,eq4],a,b,d,e,f)
$(\frac{BC-AD-(B-D)x+(A-C)y}{B-D})^2=0$
As you can see you get the double line through the two points. This is because technically a double line is tangent where it intersects.
$(ax+(-(A(S_1 + S_2) - C(S_1 + S_2) - 2B + 2D)a/(2AS_1S_2 - 2CS_1S_2 - B(S_1 + S_2) + D(S_1 + S_2)))y)^2+(-2(2A^3S_1^2S_2^2 + 2C^3S_1^2S_2^2 - 2(2S_1^2S_2 + S_1S_2^2)C^2D + 2(S_1^2 + 2S_1S_2)CD^2 - 2D^3S_1 - 2B^3S_2 - 2(CS_1^2S_2^2 - DS_1S_2^2)A^2 + (2(2S_1S_2 + S_2^2)A + (S_1^2 - 2S_1S_2 - S_2^2)C - 2D(S_1 - 2S_2))B^2 - (2C^2S_1^2S_2^2 - 4CDS_1^2S_2 + (S_1^2 + 2S_1S_2 - S_2^2)D^2)A + (2C^2S_1^2S_2 - 2(S_1^2S_2 + 2S_1S_2^2)A^2 - (3S_1^2 + 2S_1S_2 - S_2^2)CD + 2D^2(2S_1 - S_2) + (4CS_1S_2^2 + (S_1^2 - 2S_1S_2 - 3S_2^2)D)A)B)a^2/(4A^2S_1^2S_2^2 + 4C^2S_1^2S_2^2 + (S_1^2 + 2S_1S_2 + S_2^2)B^2 - 4(S_1^2S_2 + S_1S_2^2)CD + (S_1^2 + 2S_1S_2 + S_2^2)D^2 - 4(2CS_1^2S_2^2 - (S_1^2S_2 + S_1S_2^2)D)A - 2(2(S_1^2S_2 + S_1S_2^2)A - 2(S_1^2S_2 + S_1S_2^2)C + (S_1^2 + 2S_1S_2 + S_2^2)D)B))x+(2(2A^3S_1^2S_2 + 2C^3S_1S_2^2 - 2(2S_1S_2 + S_2^2)C^2D + 2CD^2(S_1 + 2S_2) - (2(2S_1^2S_2 - S_1S_2^2)C - (S_1^2 + 2S_1S_2 - S_2^2)D)A^2 + 2(A(2S_1 + S_2) - CS_1 + D)B^2 - 2B^3 - 2D^3 + (2(S_1^2S_2 - 2S_1S_2^2)C^2 - (S_1^2 - 2S_1S_2 - 3S_2^2)CD - 2D^2S_2)A - (2(S_1^2 + 2S_1S_2)A^2 + (S_1^2 - 2S_1S_2 - S_2^2)C^2 + 4CDS_2 - ((3S_1^2 + 2S_1S_2 - S_2^2)C - 4DS_1)A - 2D^2)B)a^2/(4A^2S_1^2S_2^2 + 4C^2S_1^2S_2^2 + (S_1^2 + 2S_1S_2 + S_2^2)B^2 - 4(S_1^2S_2 + S_1S_2^2)CD + (S_1^2 + 2S_1S_2 + S_2^2)D^2 - 4(2CS_1^2S_2^2 - (S_1^2S_2 + S_1S_2^2)D)A - 2(2(S_1^2S_2 + S_1S_2^2)A - 2(S_1^2S_2 + S_1S_2^2)C + (S_1^2 + 2S_1S_2 + S_2^2)D)B))y+((4(CS_1^2S_2^2 - DS_1^2S_2)A^3 - 4(CS_2 - D)B^3 - (8C^2S_1^2S_2^2 - 4(3S_1^2S_2 + S_1S_2^2)CD + (3S_1^2 + 6S_1S_2 - S_2^2)D^2)A^2 + ((S_1^2 - 6S_1S_2 - 3S_2^2)C^2 + 4CD(S_1 + 3S_2) + 4((2S_1S_2 + S_2^2)C - D(2S_1 + S_2))A - 8D^2)B^2 + 4(C^3S_1^2S_2^2 - (2S_1^2S_2 + S_1S_2^2)C^2D + (S_1^2 + 2S_1S_2)CD^2 - D^3S_1)A - 2(2C^3S_1S_2^2 - 2(2S_1S_2 + S_2^2)C^2D + 2CD^2(S_1 + 2S_2) + 2((S_1^2S_2 + 2S_1S_2^2)C - (S_1^2 + 2S_1S_2)D)A^2 - 2D^3 - (2(S_1^2S_2 + 3S_1S_2^2)C^2 - (3S_1^2 + 10S_1S_2 + 3S_2^2)CD + 2D^2(3S_1 + S_2))A)B)a^2/(4A^2S_1^2S_2^2 + 4C^2S_1^2S_2^2 + (S_1^2 + 2S_1S_2 + S_2^2)B^2 - 4(S_1^2S_2 + S_1S_2^2)CD + (S_1^2 + 2S_1S_2 + S_2^2)D^2 - 4(2CS_1^2S_2^2 - (S_1^2S_2 + S_1S_2^2)D)A - 2(2(S_1^2S_2 + S_1S_2^2)A - 2(S_1^2S_2 + S_1S_2^2)C + (S_1^2 + 2S_1S_2 + S_2^2)D)B))=0$
The other solution is the unique parabola from your data.
For example for
A=-2
B=3
C=3
D=2
S1=-2
S2=1/2
we get
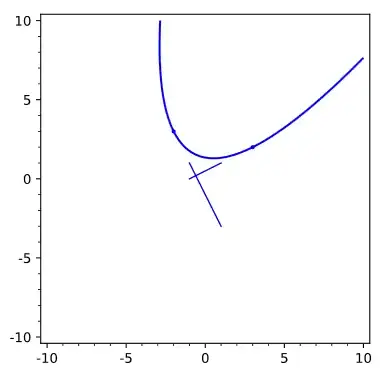
The problem is a degenerate case of the four conic sections through two points tangent to three lines in general position in ${\Bbb P}^2_{\Bbb C}$. The two points and two lines you supply are not in general position, since the points lie on the lines. But, since you seek a parabola, the line at infinity; $z=0$ is a third tangent line.
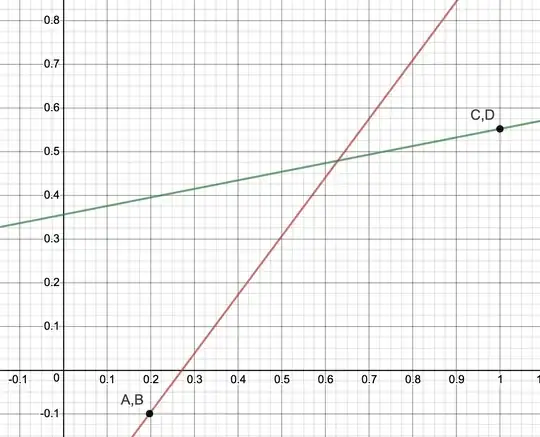

The solutions will be the double line through the two points (since this technically is tangent to anything), the all zero solution, and the equation sought.
– Jan-Magnus Økland Mar 15 '19 at 09:58