1

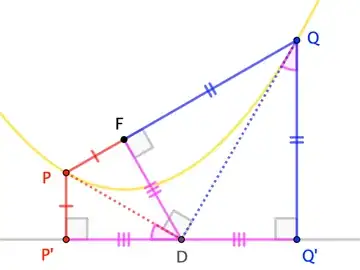
I am trying to determine the equation of directrix and focus of the parabola which has tangents $y=x$ at $(3,3)$ and $y=-x$ at $(1,-1)$. Drawing a rough picture suggest that the parabola is oblique. Also since the foot of perpendicular from focus to any tangent lies on the tangent at vertex, this implies that the line joining the focus and the foot of perpendicular to tangent $y=x$ is of the form $x+y=k_1, k_1\in\mathbb{R}$ and also line joining focus and foot of perpendicular to tangent $y=-x$ is of the form $y=x+k_2,k_2\in\mathbb{R}$.

One standard method is to consider $ax^2+by^2+2gx+2fy+2hxy+c=0$ and write the equation of tangents with point of contact $(x_1,y_1)$ as $axx_1+byy_1+g(x+x_1)+f(y+y_1)+h(x_1y+xy_1)+c=0$ for both the tangents and compare with the equation of tangents but that is rather tedious.

It is unclear on how to proceed from here. Any hints involving only the geometry of the standard parabola without involvement of linear algebra techniques are appreciated. Thanks.

Paras Khosla
  • 6,481

2 Answers2

2

From the geometry of the standard parabola, we "know":

If the asymptotes at points $P$ and $Q$ of a parabola meet at a right angle at $D$, then

  1. $D$ lies on the directrix of the parabola.

  2. Focus $F$ of the parabola lies on $\overline{PQ}$.

Further, as a consequence of the Reflection Property of the parabola, the reflection $P'$ of $F$ in asymptote $\overline{DP}$ is perpendicular to the directrix; since reflection provides that $\overline{FP}\cong\overline{PP'}$, and the definition of the parabola requires that $P$ is equidistant from $F$ and the directrix, we have that $P'$ is actually the foot of the perpendicular from $P$ to the directrix. Since $\triangle DFP\cong\triangle DP'P$, we conclude that $F$ is the foot of the perpendicular from $D$ to $\overline{PQ}$.

enter image description here

Applying this to the problem at hand ... Let the points be $P:=(3,3)$ and $Q:=(1,-1)$, and define $D:=(0,0)$.

  • One readily determines the line through $D$ perpendicular to $\overline{PQ}$, and thus also the intersection $F$ of that perpendicular and $\overline{PQ}$.
  • Easily reflecting $F$ over asymptote $y=x$ gives a point on the directrix. Since the origin is also on the directrix, finding the equation is straightforward.
Community
  • 1
Blue
  • 75,673
1

Starting from the general equation $$ Ax^2+2Bxy+Cy^2+2Dx+2Ey+1=0 $$ We can impose the conditions:

1) The line passing from $(3,3)$ and $(1,-1)$ is the polar of $(0,0)$ .

2) $(3,3) $ is a point of the conic.

3) $(1,-1)$ is a point of the conic.

4) the conic is a parabola (i.e. $B^2-AC=0$)

These give five equations in the five unknowns.

Emilio Novati
  • 62,675