I know the zeros of $f(z,w)=w-z^w$ have an analytic form:
$$\operatorname{zero}[z,n]=-\frac{W[-\log(z),n]}{\log(z)}$$
Is there a way to compute the zeros of $$f(z,w)=w-z^{(z^w)}$$?
Asked
Active
Viewed 487 times
3
-
What about Newton-iteration (for the case, where you have numerical values)? Moreover, someone I do not remember at the moment proposed to modify the question $$z^{z^w}=w$$ by one exponent of $w$ to get $$(z^{z^w})^w=(z^w)^{(z^w)}=w^w$$ and then use Lambert W, but I forget how he went on from this. – Gottfried Helms Jun 06 '20 at 00:18
-
Another link, nearly an earlier doublet of the question, with hints to further literature : https://math.stackexchange.com/questions/2490769/solutions-of-aax-x-for-fixed-a0 – Gottfried Helms Jun 16 '20 at 18:24
-
Thanks for that reference Gottfried. I'm working on the problem and will follow up here if I have something meaningful to contribute to the matter. – Dominic Jun 17 '20 at 20:34
-
My scheme seems to be not perfect; with base $I$ I get a couple of exceptions. For instance, it seems, there is no 3-periodic cycle of the index $K=[1,0,0]$ but a primitive 6-cycle of the index $K=[1,0,0,1,0,0]$ which is itself cyclic and thus should indicate to a primitive 3-cycle, twofold concatenated. Moreover, the $K=[-1,0,0]$ cycle has two solutions, and the $K=[0,0,0]$ cycle has the $K=[0]$ cycle but also a primitive 3-cycle. Don't know why those exceptions occur. I've checked the $K=[1,0,0]$ thing with Wolfram-alpha with the same result.I've a long list of cycles base $I$ available. – Gottfried Helms Jun 17 '20 at 23:53
7 Answers
2
update I give 2 solutions, but you likely do not want solution 1) because it gives only a solution where $w=z^w=z^{z^w}$.
Surely you want $z^w \ne w=z^{z^w}$; but for this I have only a Newton-iteration which is applicable only to numerical values for $z$, see solution 2). For this approach you might want to see my related questions (where only I worked with $z=\exp(1)$ as a special case) in MSE in MO. /update
To continue my comment at your question.
Solution 1)
Include one power of $w$ in your formula to get
$$
(z^w)^{(z^w) } = w^w
$$
From this we have
$$ z^w = \exp\left(W\left(\log(w^w)\right)\right) = w
$$
and then
$$ z = w^{1/w}
$$
Surely we can have more solutions, but before investing more thought one should first look whether this ansatz fits your question/intention at all...
\\ Pari/gp
ww=7 \\ take some vlue for w^w
\\ now z^w as well as w can be determined using LambertW
w=zw=exp(LambertW(log(ww))) \\ ~ 2.31645495879
z = w^(1/w) \\ from w we can determine z
[z,w,z^z^w] \\ check it
[1.43711763157, 2.31645495879, 2.31645495879] \\ see that z^z^w = w
Solution 2)
Here I use Newtoniteration on branched iterated logarithms, for an example base $z=3$. I use by default as initial value $w=1+I$ (-if you use $w=1-I$ instead you get the conjugate list but which is identical except the fixed-point using branches $[0,0]$ will find the conjugate which does not occur here).
In the table below $A$ and $B$ determine the branch-indexes for the two-fold iterated complex logarithm. I conjecture (as in my linked MSE and MO-posts): all possible 2-periodic points are in $1:1$-concordance to the $\mathbb Z^2$-fold possible solutions in this section.
Note that if $A=B$ we get the solutions $w=z^w$ which you do not want and which I've thus deleted from the list. Note also, that negating $A$ and/or $B$ gives complex conjugate solutions. Note moreover, that if $B=-A$ then the two points of the period are simply complex conjugates of each other.
Note also, the irrational numbers below for $w,z^w,z^{z^w}$ are approximations; but they are good enough to be usable for inital values for a Newton-iteration to improve them to as many decimals as you want (and as your software can...).
I get the following systematic solutions:
A B w z^w z^z^w
----------------------------------------------------------------------- -------------
... ... ....
-4 -3 2.90452432729-18.4873742793*I 2.66634530785-24.1647605084*I 2.90452432729-18.4873742793*I 3)
-4 -2 2.90098045940-12.7800357612*I 2.34205045833-24.1034322096*I 2.90098045940-12.7800357612*I
-4 -1 2.89373122666-7.07877415278*I 1.85175945825-23.9533791947*I 2.89373122666-7.07877415278*I
-4 0 2.86628764997-1.38861308938*I 1.05445194503-23.2874538247*I 2.86628764997-1.38861308938*I
-4 1 2.81443893812+4.35135182417*I 1.49755483209-21.9695929326*I 2.81443893812+4.35135182417*I
-4 2 2.80522570719+10.0980478280*I 2.13861775729-21.6936507329*I 2.80522570719+10.0980478280*I
-4 3 2.80334961243+15.8338333088*I 2.52826352812-21.6065097127*I 2.80334961243+15.8338333088*I
-4 4 2.80302075822+21.5646616935*I 2.80302075822-21.5646616935*I 2.80302075822+21.5646616935*I
-3 -4 2.66634530785-24.1647605084*I 2.90452432729-18.4873742793*I 2.66634530785-24.1647605084*I
-3 -2 2.65823419069-12.7532296409*I 2.33662843889-18.4003569977*I 2.65823419069-12.7532296409*I
-3 -1 2.64860528489-7.05765724144*I 1.83867757452-18.2606142084*I 2.64860528489-7.05765724144*I
-3 0 2.61188620485-1.37886995991*I 0.985784440913-17.5997395456*I 2.61188620485-1.37886995991*I
-3 1 2.53915979437+4.37202094411*I 1.47508951944-16.2067393371*I 2.53915979437+4.37202094411*I
-3 2 2.52898172705+10.1297287526*I 2.13515430054-15.9505021222*I 2.52898172705+10.1297287526*I
-3 3 2.52778322138+15.8715665110*I 2.52778322138-15.8715665110*I 2.52778322138+15.8715665110*I
-3 4 2.52826352812+21.6065097127*I 2.80334961243-15.8338333088*I 2.52826352812+21.6065097127*I
-2 -4 2.34205045833-24.1034322096*I 2.90098045940-12.7800357612*I 2.34205045833-24.1034322096*I
-2 -3 2.33662843889-18.4003569977*I 2.65823419069-12.7532296409*I 2.33662843889-18.4003569977*I
-2 -1 2.31413618550-7.01816313107*I 1.82057588829-12.5782846591*I 2.31413618550-7.01816313107*I
-2 0 2.25920284465-1.36256120824*I 0.883051038598-11.9323970979*I 2.25920284465-1.36256120824*I
-2 1 2.14203634901+4.41508354174*I 1.44793341004-10.4197653101*I 2.14203634901+4.41508354174*I
-2 2 2.13309499445+10.1963200289*I 2.13309499445-10.1963200289*I 2.13309499445+10.1963200289*I
-2 3 2.13515430054+15.9505021222*I 2.52898172705-10.1297287526*I 2.13515430054+15.9505021222*I
-2 4 2.13861775729+21.6936507329*I 2.80522570719-10.0980478280*I 2.13861775729+21.6936507329*I
-1 -4 1.85175945825-23.9533791947*I 2.89373122666-7.07877415278*I 1.85175945825-23.9533791947*I
-1 -3 1.83867757452-18.2606142084*I 2.64860528489-7.05765724144*I 1.83867757452-18.2606142084*I
-1 -2 1.82057588829-12.5782846591*I 2.31413618550-7.01816313107*I 1.82057588829-12.5782846591*I
-1 0 1.68477296063-1.33017692429*I 0.695312246059-6.32753593363*I 1.68477296063-1.33017692429*I
-1 1 1.42435357273+4.56471389231*I 1.42435357273-4.56471389231*I 1.42435357273+4.56471389231*I
-1 2 1.44793341004+10.4197653101*I 2.14203634901-4.41508354174*I 1.44793341004+10.4197653101*I
-1 3 1.47508951944+16.2067393371*I 2.53915979437-4.37202094411*I 1.47508951944+16.2067393371*I
-1 4 1.49755483209+21.9695929326*I 2.81443893812-4.35135182417*I 1.49755483209+21.9695929326*I
0 -4 1.05445194503-23.2874538247*I 2.86628764997-1.38861308938*I 1.05445194503-23.2874538247*I
0 -3 0.985784440913-17.5997395456*I 2.61188620485-1.37886995991*I 0.985784440913-17.5997395456*I
0 -2 0.883051038598-11.9323970979*I 2.25920284465-1.36256120824*I 0.883051038598-11.9323970979*I
0 -1 0.695312246059-6.32753593363*I 1.68477296063-1.33017692429*I 0.695312246059-6.32753593363*I
0 1 0.695312246059+6.32753593363*I 1.68477296063+1.33017692429*I 0.695312246059+6.32753593363*I
0 2 0.883051038598+11.9323970979*I 2.25920284465+1.36256120824*I 0.883051038598+11.9323970979*I
0 3 0.985784440913+17.5997395456*I 2.61188620485+1.37886995991*I 0.985784440913+17.5997395456*I
0 4 1.05445194503+23.2874538247*I 2.86628764997+1.38861308938*I 1.05445194503+23.2874538247*I
1 -4 1.49755483209-21.9695929326*I 2.81443893812+4.35135182417*I 1.49755483209-21.9695929326*I
1 -3 1.47508951944-16.2067393371*I 2.53915979437+4.37202094411*I 1.47508951944-16.2067393371*I
1 -2 1.44793341004-10.4197653101*I 2.14203634901+4.41508354174*I 1.44793341004-10.4197653101*I
1 -1 1.42435357273-4.56471389231*I 1.42435357273+4.56471389231*I 1.42435357273-4.56471389231*I
1 0 1.68477296063+1.33017692429*I 0.695312246059+6.32753593363*I 1.68477296063+1.33017692429*I
1 2 1.82057588829+12.5782846591*I 2.31413618550+7.01816313107*I 1.82057588829+12.5782846591*I
1 3 1.83867757452+18.2606142084*I 2.64860528489+7.05765724144*I 1.83867757452+18.2606142084*I
1 4 1.85175945825+23.9533791947*I 2.89373122666+7.07877415278*I 1.85175945825+23.9533791947*I
2 -4 2.13861775729-21.6936507329*I 2.80522570719+10.0980478280*I 2.13861775729-21.6936507329*I
2 -3 2.13515430054-15.9505021222*I 2.52898172705+10.1297287526*I 2.13515430054-15.9505021222*I
2 -2 2.13309499445-10.1963200289*I 2.13309499445+10.1963200289*I 2.13309499445-10.1963200289*I
2 -1 2.14203634901-4.41508354174*I 1.44793341004+10.4197653101*I 2.14203634901-4.41508354174*I
2 0 2.25920284465+1.36256120824*I 0.883051038598+11.9323970979*I 2.25920284465+1.36256120824*I
2 1 2.31413618550+7.01816313107*I 1.82057588829+12.5782846591*I 2.31413618550+7.01816313107*I
2 3 2.33662843889+18.4003569977*I 2.65823419069+12.7532296409*I 2.33662843889+18.4003569977*I
2 4 2.34205045833+24.1034322096*I 2.90098045940+12.7800357612*I 2.34205045833+24.1034322096*I
3 -4 2.52826352812-21.6065097127*I 2.80334961243+15.8338333088*I 2.52826352812-21.6065097127*I
3 -3 2.52778322138-15.8715665110*I 2.52778322138+15.8715665110*I 2.52778322138-15.8715665110*I
3 -2 2.52898172705-10.1297287526*I 2.13515430054+15.9505021222*I 2.52898172705-10.1297287526*I
3 -1 2.53915979437-4.37202094411*I 1.47508951944+16.2067393371*I 2.53915979437-4.37202094411*I
3 0 2.61188620485+1.37886995991*I 0.985784440913+17.5997395456*I 2.61188620485+1.37886995991*I
3 1 2.64860528489+7.05765724144*I 1.83867757452+18.2606142084*I 2.64860528489+7.05765724144*I
3 2 2.65823419069+12.7532296409*I 2.33662843889+18.4003569977*I 2.65823419069+12.7532296409*I
3 4 2.66634530785+24.1647605084*I 2.90452432729+18.4873742793*I 2.66634530785+24.1647605084*I
4 -4 2.80302075822-21.5646616935*I 2.80302075822+21.5646616935*I 2.80302075822-21.5646616935*I
4 -3 2.80334961243-15.8338333088*I 2.52826352812+21.6065097127*I 2.80334961243-15.8338333088*I
4 -2 2.80522570719-10.0980478280*I 2.13861775729+21.6936507329*I 2.80522570719-10.0980478280*I
4 -1 2.81443893812-4.35135182417*I 1.49755483209+21.9695929326*I 2.81443893812-4.35135182417*I
4 0 2.86628764997+1.38861308938*I 1.05445194503+23.2874538247*I 2.86628764997+1.38861308938*I
4 1 2.89373122666+7.07877415278*I 1.85175945825+23.9533791947*I 2.89373122666+7.07877415278*I
4 2 2.90098045940+12.7800357612*I 2.34205045833+24.1034322096*I 2.90098045940+12.7800357612*I
4 3 2.90452432729+18.4873742793*I 2.66634530785+24.1647605084*I 2.90452432729+18.4873742793*I
... ... ....
A picture of that $2$-periodic points follows below (this picture shows only that finite subset which are given numerically above plus the $1$-periodic points (fixed points). The set is however infinite).
Most points (blue color) are $2$-periodic, some are $1$-periodic. I've marked the $1$-periodic points (branches are $[A,B]$ with $B=A$) and $2$-periodic points which are pairs of complex conjugate values (branches are $B=-A$) with a red circle and in the second case with red straight lines.
Special cases are that $1$-periodic points with $A=B=0$. Here the initial value (positive or negative imaginary halfplanes) for the Newton-iteration is relevant for finding both fixed points.
For all other $1$-periodic points the given values for all $A=B \ne 0$ make the initial value irrelevant and we get for $A=B=+m$ and $A=B=-m$ the according complex conjugate fixed points.
And more points, making the infinitude of $2$-periodic points more visible. In this picture the $y$-axis is for better impression rescaled by $\sinh^{-1}(\Im(w)/2)/\log(3)$ which is approximate $\log_3(\Im(w))$ but allows zero and negative numbers:
Gottfried Helms
- 34,920
-
Might you explain further how you got the first line in Solution 2? I did read your reference for the case of w=e^(e^w) but cannot get your results when : A=-4, B=-3, w=2.9-18.48I for my function. When I apply your method to w=3^(3^w) I get the double-iterated log expression: 1/a[Log[1/a(Log(w)+2nPi i)]+2mPi i] with a=Log[3]. When I iterate say for 10 times, I get -0.4+4.3I. – Dominic Jun 06 '20 at 19:58
-
Hmm, when I use just the above listed digits, the sequence $w$,$w=z^w$,$w=z^w$,... degenerates in few steps. However, if I use that digits as initial values for a Newton-iteration on the branched iterated logarithms, this converges quickly to more than 100 dec digits precision.(I work internally with 200 dec digits as default in Pari/GP). Your formula looks correct (and is indeed for $z=3$), and your result might occur because a) of truncated value for $w$ taken from my protocol and/or b) of little decimal precision in your software? – Gottfried Helms Jun 06 '20 at 20:15
-
Perhaps use that w to more digits:
w = 2.9045243272916425627762319010916505569185043276815428678894457101648103987919119 - 18.487374279333954233936406981401119430419548913075364816944050737774352685449012*II get even after 20 iteration-steps w=z^z^w more than 60 digits reproduced. – Gottfried Helms Jun 06 '20 at 20:18 -
A protocol using the log-formula: $$[base=3,a=log(base)] \to [3, 1.09861228867] \ w= 2.90452432729-18.4873742793I \ w= (log( (log(w)+(-4)pi2i)/a)+(-3)pi2i)/a \to 2.90452432729 - 18.4873742793I \ w= (log( (log(w)+(-4)pi2i)/a)+(-3)pi2i)/a \to 2.90452432729 - 18.4873742793I \ w= (log( (log(w)+(-4)pi2i)/a)+(-3)pi2i)/a \to 2.90452432729 - 18.4873742793I $$ This process even improves the initial value from the first step on... Don't have an idea what's going wrong with your checking... – Gottfried Helms Jun 06 '20 at 20:33
-
I started the iteration beginning with w_0=1+i. Is that what you started with to get it to iterate to w=2.904-18.487I? – Dominic Jun 06 '20 at 20:45
-
I added my Mathematica code above to better show what I'm attempted to use for your method – Dominic Jun 06 '20 at 20:51
-
2
Without wanting to detract too much away from Gottfried's way of solving this, I'd like to point a couple of things that may be of interest to the OP: You can actually solve many transcendental equations, by defining and inverting certain more complex functions (Note that I use a slightly different notation here: solving the equation $c^{c^z}=z$, so your $z$ correponds to my given $c$) Similar to how $z=c^z$ is solved by Lambert's $W$ function which inverts the map $zc^{-z}$, when solving the equation $zc^{-z}=1$ as $z_k=\frac{W_k(-\log(c))}{-\log(c)}$. For example, you can define the map $HW$ to be the inverse of $z\exp(\log(c)\exp(\log(c)z))$, which can solve then the equation $c^{c^z}=z$ or $f_c^{(2)}(z)=z$, where the $(2)$ denotes two-fold composition of $f_c(z)$. Such inverse maps always exist, by virtue of Lagrange's Inversion Theorem, so they can calculate solutions to similar equations fast.
For example, for a given $c\in\mathbb{C}$, then a solution of $c^{c^z}=z$ will be given as:
$$z_0=\frac{HW(-\log(c);\log(c))}{-\log(c)}$$
Using the Maple code from the back of this article, for specific $c=-2-i$ this is calculated with at least 8 digits of accuracy as: $z_0\sim 0.243918+0.1945752i$. $z_0$ along with $f_c(z_0)$ will be a 2-cycle. Check: $f_c(z_0)=1.8014674-0.9762585679$, and $f_c^{(2)}(z_0)=z_0$.
In one of the later articles it is proved that such maps ($HW$) are actually multi-valued as well and are given a recursive procedure to calculate the other branches $HW_k$, $k\in\mathbb{Z}$, without resorting to numerical methods, except to improve accuracy. So, speaking generally this seems to confirm Gottfried's result that the solutions are at least countable for each $c\in\mathbb{C}$.
Edit#1:
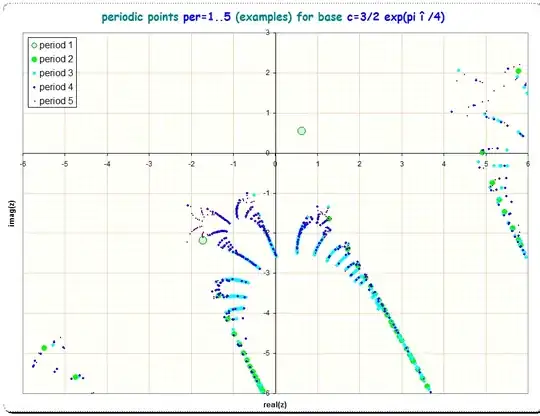
I am updating this to note an interesting connection: When I compare Gottfried's picture for 2-periodic points below in Update #5 with the actual image of the Julia Set for $g_c(z)=c^z$, for $c=3/2\exp(\pi i/4)$, the periodic points appear to be suspiciously close to the periodic fixed points on the outside layer of the Julia Set. I include a pic here for the Julia Set for this $c$, so you can discern yourself:
It appears that there are many many more, as Gottfried's correspond only to the outer recursive layer of the Cantor Bouquet. The main greenish circular feature is the fixed point of convergence of the iterated sequence $g_c^{(\omicron p)}(z)$. All greenish circular features in the Cantor Bouquet are also fixed points, but repelers. If you unwind the Bouquet down to smaller copies of itself, the pattern repeats around the sub-bouqets. This appears to suggest that there is a continuum of such points, or, all the fixed points are indexed by $\mathbb{Z}^{\infty}$.
I also checked the algorithm of my $HW$ functions, but unfortunately I cannot make it work to pick up more solutions. The problem seems to be related to the fact that the roots of the poly are far away from Gottfried's 2-periodic solutions and the algorithm picks up a wrong root - which then feeds to Newton and produces an overflow. I will try to optimize it a bit and see if I can make it work to pick up at least the roots that Gottfried has listed in Update#5.
-
Thanks for that Yiannis. Sounds interesting. Is there any chance I could get access to the article without paying for it? Also, I am confident the solutions of my problem are enumerated by k in ZxZ so I'd be interested in how the inverse HW is used to compute the solutions with k in Z. – Dominic Jun 08 '20 at 17:05
-
@Dominic, download it from here: [http://eretrandre.org/rb/files/Galidakis2005_22.pdf] – Jun 08 '20 at 17:10
-
The article which calculates all the branches of the $HW$ can be downloaded here: [http://jyotiacademicpress.org/jyotic/journalview/16/article/57/95]. – Jun 08 '20 at 17:14
-
Thanks Yiannis. The first reference gives me a site not found error and the second is caught by my virus software. Sorry. I just googled the article title and got it here at ResearchGate: https://www.researchgate.net/publication/233129552_On_solving_the_p-th_complex_auxiliary_equation_fpzz/link/5c829e66458515831f92bcb2/download – Dominic Jun 08 '20 at 17:55
-
Try this for the second article: http://jyotiacademicpress.org/jyotic/journalview/16/article/57/95. It somehow got hold of an illegal char at the end. – Jun 08 '20 at 18:04
-
Afraid that last reference is also causing problems. Can you give me the title so that I can google it? – Dominic Jun 08 '20 at 19:02
-
@dominic - I've downloaded the two articles from Yiannis' (corrected) links, and opened them with pdf-reader. Now I'm afraid about your virus-warning. Could you please give more information? (I've no antivirus sw active...) – Gottfried Helms Jun 08 '20 at 19:11
-
@Gottfried, I have Norton Anti-virus. When I click on the corrected link, Norton replies with a message stating it's a dangerous website and cautions not to go further. No offense to Yiannis. – Dominic Jun 08 '20 at 19:29
-
@Dominic - I see, thank you very much, it's at least not mentioned an actual virus-pattern on the file itself. Anyway I'll go on and try to find some free AV-software to scan the files. – Gottfried Helms Jun 08 '20 at 19:35
-
Yiannis - your 2005-article has an example with base $c=-2+1 \cdot î$ I've reproduced it with my notation $\text{newtonL}(K,base,initialvalue)$ for the basic case $K=[0,0,0]$. However, I'd already found, that for bases, which provide an attracting fixpoint for $c^z$, the Newtonalgo needs an -at least- approximative initialization (this is not needed, if $K \ne [0,0,0]$) . Your given base hase an attracting 3-periodic point and thus my routine was only successful with initial values with one significant digit. So I've to rethink how I can better express my claim involving this special cases... – Gottfried Helms Jun 08 '20 at 19:44
-
@Gottfried: Yes, that's probably because Newton's method requires an initial seed close to the domain of convergence for the routine. My routine for evaluating the $HW$ uses the roots of a high degree polynomial to pick up the first approximation. Then I feed this seed to Newton's method and cycle it 1000 times to just improve the accuracy of the root, so there's no way it can miss on virtue of the seed being off the convergence region. – Jun 08 '20 at 19:54
-
@Dominic: that's probably because the journal website is unsecure (http and not https). There's no danger going there. If you can't get it, email me @[email protected] and I'll send you a copy. – Jun 08 '20 at 19:59
-
Thanks Yiannis. I'm reviewing now your construct for HW. The Maple code seems relatively easy to convert to Mathematica which is what I use, just need to study it a bit more and practice with your examples. – Dominic Jun 08 '20 at 20:21
-
Yiannis - nice to see that plot of the Julia set. I tried to do such using Wolfram-Alpha to perhaps get it to larger precision, but didn't get it to work correctly. Concerning my "update 5" and the 13 roots: perhaps it is noteworthy that I've used internal precision of 800 or 1200 dec digits to solve for the roots of the order-511 HW-polynomial. I had to resort to Pari/GP in the version 2.12 with 64 bit machine to make this working properly. – Gottfried Helms Jun 19 '20 at 06:50
-
Yiannis - I've tried to match your Julia-set image with a list of n-periodic fixpoints for $n=1...5$ (so to show not only the $2$-periodic ones) . Per description of this please see my update 6 in my answer which you referred to ( https://math.stackexchange.com/a/3713978/1714 ). – Gottfried Helms Jun 19 '20 at 09:09
-
Gottfried: Good. It looks more than just coincidence. What's your opinion on how all these should be indexed? It appears there's a continuum of them, or $\mathbb{Z}^{\infty}$, but I may be wrong. – Jun 19 '20 at 09:45
-
My proposal was: 1-periodic $\mathbb Z^1$, 2-periodic $\mathbb Z^2$, 3-periodic $\mathbb Z^3$ ... and so on with n-periodic $\mathbb Z^n$ and $n \to \infty$ . I think this type of indexing can also be called "dense", according to the Shen/Rempe-Gillen article - but I may not understand their language correctly. My current problem is, that the apparent bijectivity between n-periodic points and the indexing has exceptions of so far un-understood nature (two cycles with same index; for some indexes no cycle at all - apparently very rare exceptions and possibly depending on base). – Gottfried Helms Jun 19 '20 at 17:45
-
Btw. I'm also collecting material with the bases $î$ but also $-1+î$ and $-2+î$ from your article to meditate on the base-specific exceptional indexes... . If you want to work with that data I can send you all so far found periodic points as well as their $K$-index-vectors. – Gottfried Helms Jun 19 '20 at 17:50
-
Well, my article won't be of much help, except possibly for up to the principal solution. I still haven't been able to tweak the algorithm to produce more branches. But even if it could, the index would be insufficient, as,as you say you need an index of $\mathbb{Z}^n$ for large $n$ and the $HW$ index only as $\mathbb{Z}$ – Jun 19 '20 at 18:46
-
Yiannis - I've just rewritten my recent post in mathoverflow. I think my ansatz (and its conjectures & problems) might be better understandable by this. If you like, see this: https://mathoverflow.net/q/361136/7710 – Gottfried Helms Jun 21 '20 at 20:13
-
Hello Yiannis, I've compiled my current thoughts, concerning the exponential function with base $e=\exp(1)$ into a manuscript. It is still in a work-on-it state, but I thought it might be helpful to show the plan even if not yet perfect. If you like see this http://go.helms-net.de/math/tetdocs/periodic_points_compact.pdf ; constructive critics much welcome and the essay shall be updated. I have seen, that prof. W. Bergweiler is still on duty, who has written a lot about periodic points of entire functions, and shall contact him, too. Perhaps he, or some student, can help to straighten things. – Gottfried Helms Jun 29 '20 at 18:47
-
@GottfriedHelms: Hi Gottfried. Looks good. I would also send a note to Robert Devaney: http://math.bu.edu/people/bob/.He may be able to verify certain bits, since he specializes on the dynamics of the $\exp$ map. – Jun 30 '20 at 08:56
-
1
I'll go ahead and post my code to better explain what I'm doing. I use Mathematica. First I define a=Log[3] as aVal=Log[3]. Then I define a twice-iterated function funB[w,n,m]. Then I use the build-in iterator NestList to iterate the function 10 times with log sheets -4 and -3 starting the iteration at $w_0=1+i$:
aVal = Log[3];
funB[w_, n_, m_] := 1/a (Log[1/a (Log[w] + 2 n Pi I)] + 2 m Pi I);
NestList[funB[#, -4, -3] &, 1. + I, 10] // MatrixForm
$$ \left( \begin{array}{c} 1.\, +1. i \\ -0.451557+4.31613 i \\ -0.442715+4.30407 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ -0.442731+4.3041 i \\ \end{array} \right) $$
And the iteration quickly settles down to w=-0.44273+43141I but that's not a 2-cycle for $3^{3^w}$
Dominic
- 440
-
Hmm, I see
aValgiven a value, andabeing used in the denominator ? – Gottfried Helms Jun 06 '20 at 20:59 -
I get your result if I insert $a=- 4$ (which means also $z=e^{-4}$ in the notation of your question) instead of $a=\log(3)$. Is there some initialization error for your routine? – Gottfried Helms Jun 06 '20 at 21:05
-
For example: $$ \text{ base=exp(-4);w=1.0+I;for(k=1,10,w= lbb(w,base,[-4,-3]));w}$$ gives your result $$ \text{w = -0.442731094143 + 4.30409989377I}$$. If I use $$ \text{base=3;w=1.0+I;for(k=1,10,w= lbb(w,base,[-4,-3]));w}$$ I get my result $$\text{w = 2.90452432729 - 18.4873742793I}$$ – Gottfried Helms Jun 06 '20 at 21:13
-
1Oh, sorry. I changed it to aVal and now it's converging to the value 2.9-18.4I. Will continue working with your method. – Dominic Jun 06 '20 at 22:26
1
I am adding this as an answer, because comments have gotten excessive on all previous answers.
Concerning the point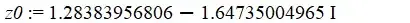 
, which is discussed in the latest comments, as it is returned by both Gottfried's and my $HW$ routine: I am getting contradictory results concerning its nature. If we assume that $c=2/3\exp(\pi i/4))$, then one easily sees that the multiplier of the iterates of the exponential of $f_c(z)=c^z$ is $t=-W(-\log(c))$ where $W$ is Lambert's function. Its absolute value evaluates to $|t|\sim 0.74019<1$, so this means the iteration $f_c^{(p)}(z)$, $p\in\mathbb{N}$ will eventually coalesce into a 1-cycle, i.e. it will converge to the limit $\frac{W(-\log(c))}{-\log(c)}$. A fairly standard result is that it will do so independent of the seed value $z_0$. In other words, it doesn't make a difference what we pick as $z_0$. The set $S=\{z_0,f_c(z_0),f_c^{(2)}(z_0),\ldots\}$, will eventually coalesce into the set consisting of only the limit point.
Now, it appears that $z_0$ as found above, is a solution of the equation $c^{c^z}=z$ or $f_c^{(2)}(z)=z$. If this was the case, however, then obviously the set $S$ would collapse to $\{z_0,c^{z_0},z_0,c^{z_0},z_0,c^{z_0},\ldots\}$, i.e. it would be a 2-cycle. I tried to discern convergence of the iterates $f_c^{(p)}(z_0)$ using Maple with 40 degree precision and I got some strange results:
5.785144579614792264675142846679492583904
+ 2.048907548090843800853209064396340249157 I
1.283839568095905609900373357729233910210
- 1.647350049596617257643000181579372962790 I
5.785144579354335186045990018486597009058
+ 2.048907548323129575849968816169365675329 I
1.283839567544272094892984866300896449236
- 1.647350049263818064433637899217191133071 I
5.785144577159479033314110704685833197627
+ 2.048907545603524369495898027514411585328 I
1.283839564487679093444240679556006245390
- 1.647350054945299642185524895899004086847 I
5.785144605442970546751824142910408759612
+ 2.048907524991945083279884030978151509106 I
1.283839622820436871810277479027898749026
- 1.647350082715293658318881014784427952819 I
5.785144797650191195472630432545489855726
+ 2.048907818044013405992884895742455414623 I
1.283839871807133148608618186790703112303
- 1.647349485584172627954396607906465200593 I
5.785141771797449707326598145083903119619
+ 2.048909595964526560002019652210728663262 I
1.283833776604257585709280414769498581842
- 1.647347289711020282645027590846904201557 I
5.785125481374699618136568156682752749168
+ 2.048878455176712548913618131118970034693 I
1.283814818403049313214359322407889757938
- 1.647409335954253674795654187904266123009 I
5.785444982437261964763977929516892487162
+ 2.048730861366547539082000145359785532536 I
1.284444850142074847418482168683545809079
- 1.647568353003458761914585661427794321578 I
5.786763338544493800046122513081622570735
+ 2.052000762407354463111485217402160000366 I
1.285714288108159351050859656404839567318
- 1.641189883938891786248816679515282720241 I
5.753453796517957705001825367047053718874
+ 2.063427200178261023873987523392904305001 I
1.222298528503810744146497616752359172709
- 1.631397201926761077667893338427954182948 I
5.650035612499114417887844540392399899343
+ 1.738580393050446935456511167370682703104 I
1.051894845321252215606676442435679034190
- 2.293166071762716720994957748633026844504 I
9.227374416634086008781996290626207545016
- 0.9597876829110760662430839626812311337642 I
75.18839490075478573478397305582549737693
+ 48.70598585354993186034362393890575641646 I
-0.0004089437332528491382532093528945655718050
- 0.0001094838220275697084074155215072070909039 I
0.9999201123461828656953225595020844254253
- 0.0003655463380775981659645966794878061462652 I
1.061154154727986406644591282120589223422
+ 1.060706527199673375826855699031006613078 I
0.2021849663284406693435370139337135443270
+ 0.6371237859445119645217753721823122454924 I
0.6016611256982373772606598767322400419739
+ 0.2666148148223991654272506922867137615728 I
0.8655038128067335246351437815453149310474
+ 0.5678509205185473269509442505245179900149 I
0.5580853508161706959531415357373418611311
+ 0.7179170041966030202341374164269666918267 I
0.5319661496565578482987841237037344135121
+ 0.4755004336272936948072845207466237655490 I
0.6997261736154818377727840172686790113734
+ 0.4896812479844500024943831589966750787667 I
0.6626390459301307531472393177444699138008
+ 0.6149798495147458203411242446663801098835 I
0.5795333960117212744990076504025242285960
+ 0.5617172516436060483917883208882177469531 I
0.6311961710286697595160988050365948909258
+ 0.5134808101341052891537025244551939604114 I
0.6578518203538736248757334801315661549241
+ 0.5585452208528633613657513847199502369873 I
0.6200203071344830007286744409888887005714
+ 0.5697214581408929548090894314592656914177 I
0.6190571250851930453542451996122487159259
+ 0.5407302165832031688023823840740735559910 I
0.6399359500940597808975076601123325553705
+ 0.5450040687623385731898264781706769523631 I
0.6331764153437664414199744718817955077588
+ 0.5593670856833985112286204415271702991227 I
0.6240762980063220444675531316964029209374
+ 0.5519000147569384484615819533790647030151 I
0.6310302988877798685719142680880899961054
+ 0.5467093875182704909763293830921573914586 I
0.6335455184285709811810786514557669382958
+ 0.5526226458918899233410401785024727959789 I
0.6288394922948805987746132501855973117338
+ 0.5533785708926950979256161708477376215874 I
0.6291356479553562284079334474228010034933
+ 0.5498664841278596091271410573447427538743 I
0.6316057703320326744759808912635819747167
+ 0.5506994148829040659418160576642921977359 I
0.6305687754301610540574549771115966920949
+ 0.5523284545006105729459819410648278164709 I
0.6295826467447454895637294231417390623440
+ 0.5512934350525084587532613932486209362880 I
0.6305009165613902339797226439988246724367
+ 0.5507686691501737549086847258305106861064 I
While it initially appears to be a 2-cycle, around the half of the table, the values change abruptly and the convergence changes into a coalescing 1-cycle. This is quite strange. As I said, if $z_0$ was indeed a 2-periodic solution for the equation $c^{c^z}=z$, then there should have been no change in the convergence behavior and the set $S$ should have remained a 2-cycle. Concluding, I have no idea what's happening with this $z_0$. Perhaps it's a pre-2-periodic but eventually 1-periodic point, which would at least explain its strange behavior. In terms of dynamics, it appears we have three attractors at play here: $z_0$ and $f_c(z_0)$ (the 2-cycle) and the limit point of the 1-cycle. As the numerical approximation of $z_0$ and $f_c(z_0)$ becomes worse through iteration, the attractor for the 1-cycle wins between the two.
Edit#1:
Concerning your comments for $z_0$. How do you get that it is a repulsive point for $\exp$? Anyway, the $\exp$ map is irrelevant here. The relevant map is $c^z$ and that's different from plain $\exp$. In any case, I think I see what's going on: You can check the multiplier of the map $f_{cc}(z)=c^{c^z}$ instead and get the following:
This is:
$$|(f_{cc})'(z_0)|\sim 10.014025>>1$$
so $z_0$ is an unstable (repulsive) fixed point for the iteration: $f_{cc}^{(p)}(z)$, $p\in\mathbb{N}$. This means that the original iteration $f_c^{(p)}(z)$, $p\in\mathbb{N}$, will be a 2-cycle only if you start at exactly $z_0$. Because you can only get an approximation of it, the iteration will gradually move way from the two repulsive fixed points $z_0$ and $f_c(z_0)$ and will coalesce into a 1-cycle, i.e., it will converge to the fixed point of $f_c(z)=z$. It doesn't matter what initial approximation you use. The error in the approximation will eventually manifest and push convergence to the attractor of the 1-cycle. So it appears that $z_0$ is a valid solution afterall. I will continue this in the afternoon to see if -similarly, the other solutions of the poly give $p$-cycles for $p>2$. I expect that there would be some, and all these are repulsive as well. Something similar happens with the solution of the equation $f_c(z)=z$: The fixed points are correctly given by: $z_k=\frac{W_k(-\log(c))}{-\log(c)},k\in\mathbb{Z}$. All $z_k$ except $z_0$ are repulsive.
Edit#2 (Concerning Dominic's last comment on the enumeration of all roots using $HW$)
Dominic, sorry, I was a bit hasty on my last comment. You can use the code in the second article to list all solutions. Make sure you note the difference between the two codes. The second article initializes as "fun:=1;" instead of "fun:=exp(x);" With that change, here's how you do it:
First, you need to define your exponential in terms of the log you use. The complex log map is multivalued, so accordingly you have to use the following to define all possible branches of the exponential. First, the multibranch Log:
Now, you can define $k$ equations to be solved, as follows. First the exponential:
Then the equation:
Then solve as:
For $k=0$ this returns the 1-period value:
, which is already checked.
Now continue by excluding this root:
And now resolve again, by:
This returns the second solution:
However, if you now continue by excluding this root, we get an overflow, which means there are no other roots for the principal branch:
This returns: 
which is rejected by overflow.
Now you can go to branch 1 of log:
which returns:
evalf(abs(fck(1, c, fck(1, c, z1))-z1));
-20
1.000000000000000485674000000000134165522 10
Now exclude this root, as before and resolve:
I get:
Check that it is a solution:
evalf(abs(fck(1, c, fck(1, c, z2))-z2));
-22
7.970129586530190428460234100205063324531 10
Repeat as per the article. I get:
Check for $z_3$:
evalf(abs(fck(1, c, fck(1, c, z3))-z3));
-22
6.120230393085432839683304733125906593712 10
and you can continue this way, until there's overflow. When you get an overflow, move to a different branch, like $k=-1$ or $k=2$, etc. You get the idea. You can thus list the solutions for all branches of the Complex Log. Again, to stress the important point here: the exponential $c^{c^z}$ will attain different values depending which branch of Log you use. What you really have is $k$ different equations for $k\in\mathbb{Z}$.
-
Hm, the 2-periodic point is repelling for the $\exp()$ function. Then with 40 digits precision only ... I don't know. In Pari/GP I use by default 200 dec digits precision. So, by iteration of the exp() function we should expect that the approximation degrades and will change into chaos. (...) – Gottfried Helms Jun 10 '20 at 04:38
-
(...) On the other hand, the result by the $HW()$ function seems to be more precise, if the polynomial is of higher order, so more $\exp()$ iterations can be made before chaos. For iteration over the branched logarithm with the branch-indexes $[1,0]$ the underlying $2$-periodic point is attracting, and is approximated by (the inexact) $z_0$ as initial value. – Gottfried Helms Jun 10 '20 at 04:39
-
With the precision of the order-$64$ polynomial the root $z_0=root[37]$ and my internal 200-dec-digits sw-precision, the iteration over the $\exp()$ function degenerates in the 21 st step to false first decimal. With internal precision increased to 400 dec digits and $HW()$-polynomial of order 128 I can iterate $z_0$ over the exponential-function 45 times until the 9 th digit becomes false. I think, this can be done to arbitray precision and thus arbitrary long iteration keeping the dec digits correct for the leading part of the number. – Gottfried Helms Jun 10 '20 at 04:57
-
With that precision the first 3 iterations of $z_0$ look like this $$ 0:1.28383956805530331096340700122756 - 1.6473500496457089705925655887528 î\ 2:1.28383956805530331096340700122773 - 1.6473500496457089705925655887519 î\ 4:1.28383956805530331096340700121873 - 1.6473500496457089705925655887506 î $$ The iteration stays correct up to the 28 'th digit for the first three iterations. – Gottfried Helms Jun 10 '20 at 05:13
-
Using the branched logarithm for the fixpoint-iteration I get with that precision and polynomial the following protocol:$$ \small{ 0:1.283839568055303310963407001227563372109 - 1.647350049645708970592565588752846479046 î\ 2:1.283839568055303310963407001227475308792 - 1.647350049645708970592565588752825007307 î\ 4:1.283839568055303310963407001227477883403 - 1.647350049645708970592565588752816329564 î\ 6:1.283839568055303310963407001227478736250 - 1.647350049645708970592565588752816629025 î\ 8:1.283839568055303310963407001227478702188 - 1.647350049645708970592565588752816712615 î}$$ – Gottfried Helms Jun 10 '20 at 05:15
1
update 6: new picture overlaid n-periodic points for p=1..5
update 5: new picture quality of approximation of roots to periodic points
update 4: new picture with roots of order 511-polynomial in HW()
update 3: see conclusion
protocol 2 - refering to a comment @YiannisGalidakis
Table 1: HW-roots on base=$3/2 \exp(\pi î/4)$ with polynomial of order 127, and 400 dec digits precision in Pari/GP I've ordered the table for smallness of error (column 6:abs(z1-z3)):
k z1 = root[k] z2=base^z1 z3=base^z2 z4=base^z3 err = abs(z1-z3)
------------------------------------------------------------------------------------------------------------------------------------------------------------
approximate periodic points / verified see next table below
------------------------------------------------------------------------------------------------------------------------------------------------------------
62 0.6303492018+0.5513155662*I 0.6303492018+0.5513155662*I 0.6303492018+0.5513155662*I 0.6303492018+0.5513155662*I 3.258190924E-82
1 1.283839568-1.647350050*I 5.785144580+2.048907548*I 1.283839568-1.647350050*I 5.785144580+2.048907548*I 9.077029772E-31
44 -1.716748618-2.188956001*I -1.716748618-2.188956001*I -1.716748618-2.188956001*I -1.716748618-2.188956001*I 4.956113615E-15
15 1.724964691-2.395015968*I 12.24313449+4.942506907*I 1.724964691-2.395015968*I 12.24313449+4.942506907*I 2.957339876E-11
14 1.972140602-2.814623679*I 18.62904406+8.045518304*I 1.981767891-2.807674994*I 18.51574518+8.225634647*I 0.01187303275
------------------------------------------------------------------------------------------------------------------------------------------------------------
litter...
95 2.505039340+2.678817258I -0.3355089377+0.02959191393I 0.8259291072-0.2122229661I 1.396759876+0.8808320069I 3.343280537
93 2.633583090+2.551949907I -0.3917190987+0.01507086473I 0.8050620955-0.2503981629I 1.455097828+0.8540656136I 3.346138630
94 2.370263502+2.799399436I -0.2870428332+0.04189581396I 0.8426725571-0.1782492089I 1.345504118+0.9000320093I 3.346628983
50 -2.520029057-2.703685957I -3.002660907-0.1988141337I -0.2640309770-0.2236098742I 1.023759232-0.3144834944I 3.352656367
...
...
Table 2: Crosscheck using Newton on the branched iterated logarithm resp. exponential
newtonEb([0,0],base) \\ 0.6303492018 + 0.5513155662*I 1-periodic k: 62 attracting for exp()
newtonLb([0,0],base) \\ -1.716748618 - 2.188956001*I 1-periodic k: 44 attracting for log(,k)
--------------------------------------------------------------------------------
newtonLb([1,0],base) \\ 1.283839568 - 1.647350050*I 2-periodic k: 1 attracting for log(,k)
newtonLb([2,0],base) \\ 1.724964691 - 2.395015968*I 2-periodic k: 15 attracting for log(,k)
newtonLb([3,0],base) \\ 1.972028808 - 2.814436942*I 2-periodic k: 14 attracting for log(,k)
newtonEb = newton on exponential (branchindexes are ignored/irrelevant)
newtonLb = newton on branched logarithms (branchindexes relevant)
Note: the initialization by the known approximate roots from table 1) was not even needed for the $[0,0]$-index-cases!
Update to table 2: increasing the order of the $HW()$-polynomial to 255 I get the additional 3 roots which approximate the according further $2$-periodic points (by comparing with the Newton-iteration on the branched iterated logarithm):
newtonLb([ 4,0],base) \\ 2.141681046 - 3.108582204*I 2-periodic
newtonLb([ 5,0],base) \\ 2.270468331 - 3.335544479*I 2-periodic
newtonLb([-1,0],base) \\ -1.353190085 - 3.554170025*I 2-periodic
Here is a picture showing the incidence of the roots of the order-$255$-polynomial of the $HW()$ and the 2-periodic-points as been found by the branched iterated logarithms. $8$ $HW()$-roots coincide usefully with the b.i.log. - solutions. Don't know what to say about the other roots... :
And to see the effect of increasing the polynomial order in the $HW()$ - function for its power to approximate the 1- and 2-periodic points, I show an overlay of plots for roots of polynomial orders 31,127,255,511 with the $K=[k_1,0]$ indexed periodic points. The $HW()$ can only detect as many periodic points as lay in the interior of the hullcurve of its set of roots (with decreasing approximation towards the hullcurve).
The newly detected 2-periodic-points are as follows (values polished by Newton-iteration):
newtonLb([ 6,0],base) \\ 2.374114666 - 3.520442220*I 2-periodic
newtonLb([ 7,0],base) \\ 2.460769008 - 3.676481185*I 2-periodic
newtonLb([ 8,0],base) \\ 2.535185416 - 3.811476996*I 2-periodic
newtonLb([ 9,0],base) \\ 2.600374437 - 3.930442789*I 2-periodic
newtonLb([-2,0],base) \\ -1.126755328 - 4.141593860*I 2-periodic
newtonLb([-3,0],base) \\ -0.9683788693- 4.514449628*I 2-periodic
(update 5) To shed some light on the quality of the roots as indicators of the period-points I show a short table with the 14 usable roots $z_1=root[k]$ and the difference to $z_3=base^{base^{z_1}}$
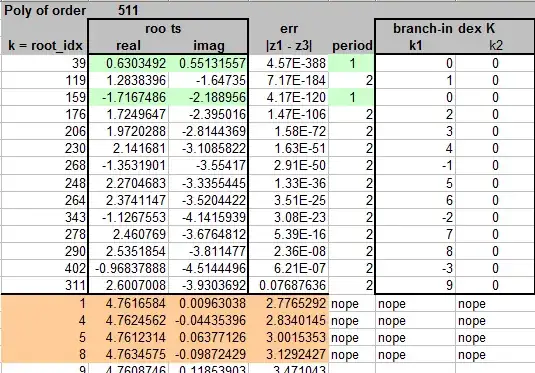
To compare with the 31-order polynomial we find 2 roots as usable indicators nearby two periodic points. The third I've marked with question-marks: this root is not inside the circular-curve, gives a significant error by iteration and comparision $|z_1-z_3|$ and should possibly not been accepted as an initial value for a follow-up Newton-iteration.
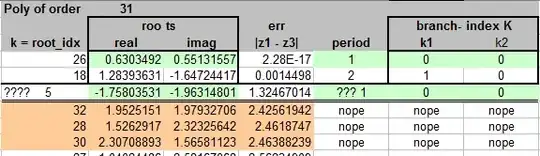
There is more on MSE on zeros of truncated exponential series which may be useful for understanding the effects in the case of the $HW()$-function, see here for a start, and perhaps this answer of mine on some observations.
/end update
Update 6: To illustrate more that the branched iterated logarithm-mechanism agrees better with the image of the Julia-set when we do not look at 2-periodic points alone, I've added a picture which includes all n-periodic points for n=1..5 which I've found by simply scanning the complex square at origin from $4+4î ... -4-4î$ in steps of $1/20$ and applying the Newton algorithms for periodic points from periods of 1 to 5 separately.
Of course this documents not all existing periodic points there, only which I found by that specific screening. Moreover, to have a smoother visual impression, I reduced the list of points to that which are in the complex square at origin from $6+6î ... -6-6î$.
All so found periodic points agreed with the branched iterated logarithm scheme, where however for at most 2 exemplars in each n-periodic list there was no uniqueness (meaning: two different cycles with the same vector of branch-indices $K$). For that type of special cases I've not yet an explanation or formalization.
/end update6
Conclusion (with update): from $HW()$-polynomial order from 15, 31, 63,127,255,511 one can see, how the set of roots form roughly an ellipse and of increasing radius. For that orders, the $HW()$ roots which are very near to 2-periodic points are always inside the built ellipse, and as many of the ellipse encloses, as many are also well approximated and can be said to be "detected".
I expect, that theoretically increasing the HW-polynomial infinitely (as well as the internal decimal precision, of course...) would give all 1- and 2-periodic points according to the indexes $K=[A,B]$ with $A \in \mathbb Z,B=0$ where only for the case of $K=[0,0]$ the newtonEb()-function is needed to identify the attracting fixed point.
P.s. just to avoid misunderstandings: "exponential" means here generally $z_1=\exp(a \cdot z_0)$ where $a=\log(c)$ and $c$ the base of "exponentiation" in contrast to "branched logarithm" which iterates $z_1 = {\log(z_0)+k \cdot 2 \pi î \over a}$ .
Gottfried Helms
- 34,920
-
1Gottfried, May I ask you if I understand correctly, your analysis above? As I see it, the HW roots produce an abundance of extraneous roots which are not solutions to the 2-cycle expression c^(c^z)=z. In fact, none of the HW roots on the circular regions are solutions. Or is it necessary to use the HW roots in a Newton iteration to find the actual roots to the 2-cycle equation? – Dominic Jun 11 '20 at 12:42
-
@Dominic - The proximity of the roots to the true 1- and 2- periodic points is very well for the innermost points and degradates for the 2-periodic points near the circular bound. With the 511-order polynomial the best proximity of the root and the respective periodic-point was 1e-311 (innermost), and the worst about 0.03 (near circular "curve"). With the 31-order polynomial the three valid proximities were between 1e-11 (inner most) to 0.3 or so (near the boundary curve). (This was always computed with 400 dec digits precision for sw-arithmetic) – Gottfried Helms Jun 11 '20 at 14:45
-
If needed I can provide my data as Pari/GP or the data for pictures as excel-file, btw... – Gottfried Helms Jun 11 '20 at 14:47
-
@Dominic - I've inserted a screenshot of the relevant part of my Excel-file for the "good" roots of the 511-order polynomial for $HW()$. The first two roots might be taken as given, but all other roots I'd polish with Newton-iteration towards best approximation to the periodic points. – Gottfried Helms Jun 11 '20 at 15:14
-
@GottfriedHelms You have 3 answers in this thread. Maybe you can merge 1 or 2 of them? – Тyma Gaidash May 14 '23 at 13:31
-
@TymaGaidash - I would like to be helpful here (MSE) and to brush up & compactify, or even simply connect, my answers. Unfortunately I feel rather worn out currently and I even have difficulties to follow the flow of Question and Answers in this thread. Anyway, I'll take your suggestion with me and may be when I'm again better with mental energy I'll come back to this. - - - But even, if you feel to be able to condense the three answers with good faith and make one fluent one - feel free and try: I'd like to see any improvement of my work. – Gottfried Helms May 14 '23 at 14:23
0
Spend some time reviewing Yiannis' paper on solving for the roots of the complex auxiliary equation and adapting the method to my problem $w=z^{z^w}$. The method, if I understand it correctly, computes a Taylor series for the auxiliary equation at the origin and then uses the smallest zero in absolute value as the starting point in a Newton iteration for the root of the aux equation. This is my code in Mathematica:
hyperW[args_, var_, nMax_] :=
Module[{auxEqn, g, taylorF, theZeros, smallestZero, theRoot},
(*
create the auxiliary equation
*)
auxEqn = Fold[Exp[#1 #2] &, Exp[z], Reverse@args];
g[z_] := z auxEqn - var;
(*
create a Taylor series for the aux equation centered at zero
*)
taylorF[z_] := Normal@Series[g[z], {z, 0, nMax}];
(* solve for the zeros of the taylor series *)
theZeros = z /. NSolve[taylorF[z] == 0, z];
(*
now find smallest root of the Taylor series -- not sure why
*)
smallestZero = theZeros[[First@Ordering[Abs /@ theZeros, 1]]];
(*
solve for the root of the aux equation
*)
theRoot = z /. FindRoot[g[z] == 0, {z, smallestZero}];
theRoot
];
I've only checked if for my expression:
theZ=3/2 Exp[Pi I/4];
auxRoot=hyperW[{-Log[theZ]},Log[theZ],10]/Log[theZ]
theZ^(theZ^auxRoot)
Out[140]= 0.630349 +0.551316 I
Out[141]= 0.630349 +0.551316 I
Dominic
- 440
-
It looks ok. Note that the solution you get is a fixed point of period 1. Not 2. For your $z$ apparently there are no solutions of period 2. – Jun 09 '20 at 17:23
-
It's not really necessary to consult the second article. To pick the other branches, just order the solutions of the poly by increasing abs and index them. Your principal branch solution is the one of smallest value. The rest will be branches 1,2,3, etc. – Jun 09 '20 at 17:27
-
There is a $2$-periodic fixpoint not too far away, $$ p_1=1.28384 - 1.64735 î \phantom{=p_1}\ p_2=5.78514 + 2.04891 î \phantom{=p_1}\ p_3=1.28384 - 1.64735 î =p_1$$. However, this is one with my indexing
p_1=newtonEb([1,0],base)and I did not yet understand, how the $HW()$ would find it (didn't see the slot for the branch specific parametrization)?(ah, just observed @Yiannis' 2nd comment when composed my) – Gottfried Helms Jun 09 '20 at 18:26 -
I believe there are ZxZ enumerated 2-cycle points for all z except at the singular points. – Dominic Jun 09 '20 at 18:26
-
Yes, Dominic, I think now, that (only!) the case of
newtonEb(K,base)ornewtonLb(K,base)(for exp() or log() iteration) with $K=[0,0,...,0]$ is ambiguous with my method, namely when the base $z$ has attracting $k$-periodic points with $k \gt 1$ – Gottfried Helms Jun 09 '20 at 18:30 -
@Yiannis, May I ask if you know of anyone that has made a systematic compilation of a group of 2-cycle roots of z^(z^w)=w using the hyper-Lambert functions? For example, say z=2 Exp[Pi I/4], computing roots (0,m) through (10,m) with m running from -100 to 100? – Dominic Jun 09 '20 at 18:45
-
@Dominic: It may be that a period 2 fixed point is picked up from another branch, other than the principal one. I cannot check this as I'd have to modify the code in Maple. You can check by looking at the solutions of the Poly in your code. I'll try to modify my code to see if I get anything interesting, but I am not so sure about whether your conjecture is true. Re: there are ZxZ enumerated 2-cycle points for all c. This needs to be proved. – Jun 09 '20 at 18:45
-
@Dominic: There is a region on the Complex Plane with c (your z), where the iteration of $f_c(z)$ is always a 2-cycle. This region is shown on fig. 4 p.989. in the article. I don't know if there are any other $c\in\mathbb{C}$ such that $f_c(z)$ is always a 2-cycle. I don't think we currently know. This region is shown in Daniel Geisler's Tetration side: http://www.tetration.org/. it's the small yellow circle, left and with contact with the red nephroid central region. If you interpret "yellow" as period 2 in Daniel's map, then it looks like there are other regions as well. – Jun 09 '20 at 18:54
-
@Yiannis: I am actually very familiar with that diagram you speak of: It is a cycle diagram for a tetration iteration z^z^(...) and shows only the regions were that iteration, after a finite number of iterations converges to cycles of various lengths, or diverges. However, it is not a diagram of the solutions of z^(z^w)=w. – Dominic Jun 09 '20 at 19:08
-
@Dominic: yes, of course. But note that the solutions you speak of, naturally depend on $c$ (your $z$). If you pick a $c$ and the iteration $f_c(z)$ goes into a $p$-cycle for $p>2$, you can't get 2-period solutions for your equation. That's obvious. If you get such a solution, it means your $c$ you picked forces a $p=2$ cycle and that's impossible. So the period of the iteration DEPENDS on $c$, not the other way around. You CANNOT get solutions of different period than what the iteration for $f_c(z)$ and thus $c$ specifies. That would be impossible. – Jun 09 '20 at 19:30
-
Don't know, whether this is useful for this discussion, but I did this also for my own understanding. I followed the HW-idea and created the truncated powerseries, handled it as a polynomial $p(w)$ of order 31 and computed the roots $p(w)-\log(z)$. Two from that 31 roots were (approximately) member of periods, namely of $1$- and $2$-periods. I've made another answer to show the protocol. I found it instructive. If you feel it is trivial I can also delete it. – Gottfried Helms Jun 09 '20 at 20:03
-
@Dominic: Sorry, I forgot to answer your question: No, I am not aware of any systematic compilation of periodic 2 point solutions using the HW functions. There have been some publications which use the functions but for solving other transcendental equations in Physics. – Jun 10 '20 at 09:30
-
Thanks for that Yiannis. The reason I asked is because I attempted to compile such a list but quickly ran into "Overflow" after only a few iterates using the method from your second reference,"On the Enumeration of roots using HW function" which I found on ArXiv. – Dominic Jun 10 '20 at 11:29
-
I added a new "answer" with a protocol on the usability of the $HW()$-roots when precision and order of polynomial is high enough. Subsets in the found roots are near the list of roots as gotten by the branched iterated logarithm, and it looks, that the coincidences are even improving when the precision and and the polynomial is improved. – Gottfried Helms Jun 10 '20 at 12:40
-
@Dominic: Sorry, you cannot use the code in the second article for enumerating the roots, because the code is different from that in the first article. It has been adapted for use with general transcendental equations, not just of the $\exp()$ kind. For the equation $c^{c^z}=z$ it's better to use the code in the first article. – Jun 10 '20 at 18:19
-
@Dominic: Please see Edit#2 on my answer below. I was mistaken in my previous comment. You can list all solutions using the second article code. On the Edit I show how it's done. – Jun 10 '20 at 20:14
-
Thanks for that Yiannis. It's a very nice construct, the hyper-W as you defined it. I'll go back and work more with it. – Dominic Jun 11 '20 at 00:38
0
This is not a real answer, just another protocol as mentioned in my comment at Dominic's answer.
The list of roots of the order-31 polynomial taken from the truncated taylorseries for $f(w)=w \lambda \cdot z^{-z^w}$ where $\lambda:=\log(z)$ to solve for $f(w)=\lambda$.
In the rows the iterations according to $z=3/2 \cdot \exp(\pi î /4)$ up to $3$'th iteration is shown to make visible the solutions with periodicity.
The two roots, which are also periodic points are over-/underlined
k z0=root(k) z1=base^z0 z2=base^z1 z3=base^z2
--------------------------------------------------------------------------------- -----------------
1 -0.609790-2.57599*I 0.279787-5.89915*I -65.1732-94.9861*I -1.37506E20-8.25698E20*I
2 -0.0894389-2.63507*I 3.19936-6.93712*I 812.358-251.281*I -2.74051E228+5.05292E228*I
3 -1.11274-2.40054*I -1.14548-4.03693*I -12.3131-8.51648*I 4.62792-2.88525*I
4 -1.51268-2.10770*I -1.28862-2.52522*I -1.93310-3.85156*I -9.38676-0.579573*I
5 -2.29346-1.51084*I -0.965217-0.859828*I 0.594583-1.18786*I 3.23465-0.0473986*I
6 -1.86762-1.88512*I -1.26441-1.62789*I -0.176871-2.14358*I 2.67394-4.23919*I
7 -2.59359-1.00151*I -0.587508-0.493361*I 0.916125-0.713167*I 2.30704+1.05906*I
8 -2.75815-0.440056*I -0.322729-0.330252*I 1.05289-0.429570*I 1.70598+1.30434*I
9 -0.795315+2.67125*I 0.0797016+0.0393354*I 0.998336+0.0785775*I 0.965601+1.02648*I
10 -0.233844+2.77099*I 0.0608727+0.0833278*I 0.956862+0.0782497*I 0.982251+0.978030*I
11 -1.32520+2.45806*I 0.0846817-0.00374126*I 1.03579+0.0674126*I 0.962542+1.07565*I
12 -2.79508+0.138287*I -0.155469-0.243417*I 1.10912-0.248955*I 1.36845+1.32735*I
13 -2.70971+0.708251*I -0.0510161-0.184166*I 1.12453-0.129598*I 1.17798+1.28973*I
14 -2.20079+1.73040*I 0.0544672-0.0900634*I 1.09724+0.00686979*I 1.00716+1.18072*I
15 -2.50839+1.24638*I 0.0143868-0.135118*I 1.11740-0.0486222*I 1.06893+1.23634*I
16 -1.80057+2.14002*I 0.0766710-0.0466348*I 1.06915+0.0441900*I 0.974831+1.12689*I
------------------------------------------- ---------------------------------------------------
17 1.28393-1.64714*I 5.78406+2.04954*I 1.28166-1.64657*I 5.77933+2.03777*I
------------------------------------------- ---------------------------------------------------
18 1.36759-2.20500*I 9.67955+1.76194*I -5.66508+11.3564*I 0.0000132912+0.00000208076*I
19 0.917525-2.43569*I 9.47775-2.59211*I 355.212+39.0907*I 1.46153E49-7.54937E48*I
20 1.83712-2.03847*I 8.52119+6.03645*I -0.265258+0.0776230*I 0.831736-0.148654*I
21 0.426715-2.58667*I 6.85396-5.93496*I -1680.23+279.646*I 5.46811E-392+5.86744E-393*I
22 2.90504+0.0851169*I -2.06008+2.23217*I 0.0568387-0.0491431*I 1.06326+0.0262840*I
23 3.01163-0.566879*I -2.83241+4.47109*I 0.00867524-0.00378804*I 1.00650+0.00531196*I
24 2.75281+0.649339*I -1.38288+1.20376*I 0.183276-0.124858*I 1.18295+0.110714*I
------------------ --------------------- ---------------------- -------------------------
25 0.630349+0.551316*I 0.630349+0.551316*I 0.630349+0.551316*I 0.630349+0.551316*I
------------------ --------------------- ---------------------- -------------------------
26 0.887167+2.62178*I -0.0343458+0.179533*I 0.855576+0.0392292*I 1.05982+0.870925*I
27 1.39972+2.38251*I -0.128881+0.238995*I 0.786650-0.00339767*I 1.12547+0.797479*I
28 0.335048+2.75382*I 0.0250176+0.129334*I 0.910251+0.0657330*I 1.01293+0.927797*I
29 2.23289+1.63776*I -0.511919+0.452470*I 0.555982-0.123511*I 1.27861+0.520485*I
30 2.53227+1.16682*I -0.868517+0.701832*I 0.373598-0.156883*I 1.28153+0.299809*I
31 1.85307+2.04889*I -0.278145+0.320120*I 0.692024-0.0615140*I 1.20677+0.688666*I
One sees in row 17 the (approximation to) 2-periodic point, which I'd found in my earlier comment (with vector of branchindexes $K=[1,0]$ in my notation-style) and in row 25 the 1-periodic point which was already computed by Dominic ($K=[0,0]$ in my notation).
update Just to increase the precision of the $HW()$-process, I used the polynomial to order $63$. Now the periodic points occur at index 37 and 63 in the Pari/GP output. Even better approximations:
root_index z_n
37 1.28383956805-1.64735004965*I =z1 2-periodic point
5.78514457960+2.04890754805*I =z2=c^z1
1.28383956808-1.64735004968*I =z3=c^z2~z1
5.78514457976+2.04890754816*I =z4=c^z3~z2
63 0.630349201759+0.551315566237*I =z1 1-periodic point
0.630349201759+0.551315566237*I =z2=c^z1~z1
0.630349201759+0.551315566237*I =z3=c^z2~z1
0.630349201759+0.551315566237*I =z4=c^z3~z1
Gottfried Helms
- 34,920
-
Gottfried, did you pass the resulting roots of the poly to Newton's Method or are they just the roots? Row 17 seems only to be approximately a 2-cycle. When I check the multiplier of $c=3/2\exp(\pi i/4)$, I get $|t|=|-W(-\log(c))|\sim 0.74019<1$, which means the iteration $f_c(z)$ will be a 1-cycle. I.e., it converges to $-W(-\log(c))/\log(c)$. Try to pass it through Newton as well and see if you get increased accuracy, because it being approximate here I don't think it means very much. I cannot tell just by inspection. Thanks. – Jun 09 '20 at 20:45
-
@Yianis - just the pure output of the root-solver. It is very near to the $2$-periodic point in my other comment at Dominics answer (5 digits or so). That other number indeed was polished with Newton-iteration. update here is the Newton-polished number
1.28383956806 - 1.64735004965*Igotten by root_17 as initial value. – Gottfried Helms Jun 09 '20 at 20:47 -
Can you please also pass it through Newton with this value as a seed to see if you get a better accuracy? Thanks. I'd be curious to see what Newton says about it. – Jun 09 '20 at 20:50
-
@Yiannis - editing my previous comment crossed with your question. Please see the previous comment, the data are there now. (btw. the same result whether I use $f:=\exp()$ for the Newton-iteration or $f:=\log(,k)$ ) – Gottfried Helms Jun 09 '20 at 20:52
-
@Yiannis - even with the simple fixed-point iteration using the branched iterated logarithm there is quick convergence to a good approximation: $$r_{17}=1.28393-1.64714î \ r_{17}=\text{lbb}(r_{17},c,[1,0])\ *** 1.28386007329 - 1.64736010341î\ *** 1.28383846447 - 1.64735204536î\ *** 1.28383937443 - 1.64734992976î\ *** 1.28383958096 - 1.64735003092î\ *** 1.28383956986 - 1.64735005103î\ *** 1.28383956791 - 1.64735004982î\ *** 1.28383956804 - 1.64735004963î\ *** 1.28383956806 - 1.64735004964î\ *** 1.28383956806 - 1.64735004965î\ \vdots $$ – Gottfried Helms Jun 09 '20 at 21:07
-
just one more observation: the naive fixpoint-iteration with the branched iterated logarithm gives one more correct digit per iteration. (Of course, Newton-iteration gives quadratic improvement of approximation, but sometimes a preconditioning of the Newton by simple fixpoint-iteration is advised for branchidexes of the type $K=[0,0,...,0]$ for sets of bases, when the base provides attracting n-periodic points for the $\exp()$ function. (I say this because of some heuristics) – Gottfried Helms Jun 10 '20 at 09:33
-
@Yiannis - I added a new "answer" ("protocol 2") with a protocol on the usability of the $HW()$-roots when precision and order of polynomial is high enough. Subsets in the found roots are near the list of roots as gotten by the branched iterated logarithm, and it looks, that the coincidences are even improving when the precision and and the polynomial is improved – Gottfried Helms Jun 10 '20 at 12:42
-
Gottfried, what do you make of the other roots (all rows except 17 and 25)? They do not appear to be 2 or 1 cycles, so what do you do with them? Do you reject them in your root-finding algorithm? Thanks. – Jun 10 '20 at 17:50
-
@Yiannis - I'm not sure. At the moment I assume, that they are leagal roots of the polynomial; so if we insert them in the polynomial-formula instead of the intended exponential-iteration, they'll show that they are roots. But polynomial/truncated Taylorseries is not equal to the original Taylorseries of our target-function $ z a \exp(-a \exp(a z) = a$, so they are roots more or less "far" away from the solutions of the target function - and so we can throw them away. (...) – Gottfried Helms Jun 10 '20 at 18:21
-
(...) In the set of 127 polynomial roots only 5 had an error $abs(z_1-z_3)$ less than 1 - and that were good germs for finding the target-function roots using Newton-iteration starting from them. The errors of the other polynomial roots were $3 .. x e125$ and more. For the 255-order polynomial only $8$ have been good germs for the Newton-iteration, and 247 were unusable so far. Could not yet make any more sense of it myself... – Gottfried Helms Jun 10 '20 at 18:25
-
@Yiannis - please see the picture in my updated other answer. It shows the coincidence of the 2-periodic points and the roots of the $HW()$-function with 255-order polynomial. $8$ roots are well approximations of the 2-periodic points with $K=[A,0]$ with $A=-1 .. 5$. – Gottfried Helms Jun 10 '20 at 19:36
-
Gottfried, so in summary, how many valid solutions does your method return for the principal branch of log? I mean without using $2k\pi i$ in your branched log iteration. Can you list them so I can check them by hand? I am a little curious. Thanks. – Jun 10 '20 at 20:23
-
This asks for the solutions of
newtonEb(K,base)respnewtonLb(K,base)with $K=[0]$ or $K=[0,0]$ or $K=[0,0,0]$ etc. In the current state both function calls give back simply the fixpoint iteration via $z_{k+1} = c^{z_k} = \exp(a z_k)$ resp $z_{k+1} = \log( z_k)/a $ (where $a=\log(c)$). Those initial iteration are polished by a Newton-iteration. So either I get one $1$-periodic point by both procedures or two such fixed points, where in the latter case one is attracting (found withnewtonEb()) and one is repelling (vianewtonLb()) . (...) – Gottfried Helms Jun 10 '20 at 20:32 -
(...) Cases of base $c$ which have, for instance, an attracting $3$-periodic point (and are still cases of $K=[0,0,0]$) are not yet handled by my routine correctly (it finds a single repelling fixedpoint) and I'm simply trying to improve by manual finetuning (better preconditioning, possibly switching off the Newton-iteration completely,...) . Before I implement an automated solution for this specific cases where all iterated logarithms have branchindex $=0$ I think I'll have to understand the problem more exhaustive. – Gottfried Helms Jun 10 '20 at 20:37
-
(...) In the answer with $c=3/2 \exp(\pi /4 î)$ I gave the two fixed points found by me with approximation: $$ \phantom a $$
newtonEb([0,0],base) \\ 0.6303492018 + 0.5513155662*I 1-periodic attracting for exp()$$ \phantom a $$ andnewtonLb([0,0],base) \\ -1.716748618 - 2.188956001*I 1-periodic attracting for log(,k)– Gottfried Helms Jun 10 '20 at 20:44 -
Sorry, I am a little confused. Reading back and forth is becoming tedious. So, do you get any other fixed points - possibly of period $p\ge 2$, for $k=0$, except the two: $z_0=0.63034+0.55131i$, $z_1=1.28383-1.64735i$? I mean for $k=0$ in your iteration. – Jun 10 '20 at 20:59
-
If the vector of branch-indexes has length 1 ($K=[k_1]$) I get 1-periodic (=fixed-) points, namely the two you mention. If the vector of branch-indexes has length 2 ($K=[k_1,k_2]$) I get 2-periodic points, and so on. If the $k_i$ in the vector $K$ are all zero, the routine finds the 1-periodic points like when $K=[0]$. In case there are actually n-periodic points when $K=[0,0,...,0]$ with n zeros is given, then I have to supply initial values for the newton-iteration to detect them. (...) – Gottfried Helms Jun 10 '20 at 21:13
-
(...) For instance, in your article you have base $c=-1+I$ then I need
newtonEb([0,0,0],c,z0)with $z_0$ a good initialization to find the attractive 3-periodic point. If I would ask fornewtonEb([0,0,0],c)it would find the repelling 1-periodic point0.3113298680 + 0.3605363006 î(in the current simple implementation) – Gottfried Helms Jun 10 '20 at 21:19 -
I just noted this, and it may be interesting to how it applies for your algorithm. Note that all fixed points $-W_k(-\log(c))/\log(c)$ of period 1 are solutions to the equation $c^{c^z}=z$, so $\mathbb{Z}$ is indexed once already in the solutions. Can you produce a similar (to your answer in protocol 2) graph ONLY for fixed points of period 2 with your method? It'd be interesting to see how many roots are indexed this way, separately. Thanks. – Jun 11 '20 at 10:38
-
@Yiannis - perhaps the newly appended table in my current answer, (update 5) is informative enough for your question. If not, just ping me, but it might be possible I'll be active on this in the evening only. – Gottfried Helms Jun 11 '20 at 15:23