How to find examples of periodic points of the (complex) exponential-function $z \to \exp(z)$?

Question

Background: By considering the question which asks whether a certain summation-method $\mathfrak M$ for the (extremely divergent!) sum $\mathfrak M: S(z)=z + e^z + e^{e^z}+e^{e^{e^z}} + ...$ might be valid, I had the idea, that a good test for the validity of the summation-method would be to compare one result with cases, where the sum can be given on some standard way. For instance, if $z$ is a fixpoint $p$ of $\exp(z)$ having $\exp(p)=p$ then $S(p) = p + p+ p+ p+...$ which could possibly been evaluated using the $\zeta(0)$ - definition.
But this is possibly no good test, a better one were, if for instance $p$ were a $2$- periodic point where the sign changes, (let's denote a fixpoint $p_1$ and a $2$-periodic point $p_2$) such that $\exp(p_2)=-p_2$ and the series becomes $S(p_2)=p_2 - p_2 + p_2 - ... + ...$ which can then be assumed to be the Cesarosum of the alternating series of a constant.

First steps of my own approach: This led to the idea to find such $2-periodic$ points to have example cases. What I've done so far was to screen segments of the complex plane , say a square around some $z_0$ of size $2x2$ in steps of $1/10$ and find local minima. Then take each local minima of the error ($|z_0 - e^{e^z}|$ as new center of a new square with $0.2 x 0.2$ size, and iterate this two or three times until the error is small enough and then use Newton-iteration to finally find a point $p_2$ (hopefully meeting the requirements for Cesaro-summability!).

This gave by tedious manual screening an initial set of $2$-periodic points. But all so far found $2$-periodic points were on the real-positive halfplane and so not suited for Cesaro-summation of $S(p_2)=p_2-p_2+p_2-...$ with alternating signs.

Here is a picture which included a couple more points which I found by extrapolating linear trends in subsets of the found ones. See my initial answer here

Question 1:

So my first question is now for ideas,
- 1) how could I improve the search-routine? (Perhaps avoiding that manual screening at all)

The extrapolation-idea is very useful and allows to find infinitely many more $2$-periodic points completely automatically, but it still needs an initial manual screening to get at least $3$ points as germ for the extrapolation.

Question 2:

The picture contain no pairs of $2$-periodic points having alternating signs on the real part.
I've tried to find analytically better solutions, of to even prove there are no such points, but arrived nowhere definite so far.
- 2) Are there really no $2$-periodic points with negative real part?

Question 3 & 4:

If there are indeed no such cases, what about $3$-periodic points or in general $n$-periodic points?
- 3) Are there $n$-periodic points with negative real part?
- 4) Is there any analytical method known how to find $n$-periodic points without manual screening? (For the finding of $1$-periodic (or "fix"-) points we have the Lambert W-function. For generalizing the Lambert W I had found a scheme giving power series, but which have extremely small range of convergence and I think are thus useless here)

Answer 1

The structure of the periodic points of the exponential map is well-understood. Observe that the real axis is invariant and contains no periodic points; its preimages contain the horizontal lines at imaginary parts that are integer multiplies of $\pi$.

Consider the strips $$ S_k := \{ a + ib\colon (2k-1)\pi < b < (2k+1)\pi\}.$$

Every periodic point $z$ has an "itinerary" $(k_n)_{n=0}^{\infty}$, defined by $$ f^n(z) \in S_{k_n}.$$ (Here $f$ is the exponential map and $f^n$ its $n$-th iterate.)

Clearly the itinerary is a periodic sequence whose period divides the period of $z$.

It is known that every periodic sequence is realised by a periodic point. When $(k_n)_{n=0}^{\infty}$ is not the sequence $k_n \equiv 0$ for all $n$, this periodic point is unique and, in particular, has the same period as $(k_n)$.

For the sequence defined by $k_n\equiv 0$, there are two fixed points, one in the upper half-plane and one in the lower half-plane, which are complex conjugates of each other.

The periodic point for a given itinerary can be obtained by backwards iteration, as you mention. That is, let $L_k\colon \mathbb{C}\setminus (-\infty,0]\to S_k$ denote the inverse of the map $f|_{S_k}$. If $z\notin\mathbb{R}$, then define $$ z_m := L_{k_0}(L_{k_1}(\dots(L_{k_m})\dots)).$$

Then the sequence $z_m$ will converge to a periodic point with the desired itinerary, and this point is unique, except for the exceptional case $k_n\equiv 0$, where it depends on whether $\operatorname{Im} z$ is positive or negative.

It is also known that every periodic point as above, except for the case $k_n\equiv 0$ has a periodic curve to $\infty$ attached to it, periodic of the same period. This curve is called a "Devaney hair" or "external ray", and all points except the periodic endpoint converge to infinity under iteration.

I think that all of this can already be found in the paper by Devaney and Krych (Dynamics of $\exp(z)$, ETDS, 1984). They use a somewhat different convention for itineraries, but the results are equivalent.

Answer 2

As you may remember, you need to solve in general the $p$-th auxilliary exponential equation to find the fixed points first. The first auxilliary is $f(z)=z$, with $f=exp$. This is solved by using Lambert's $W$ function as $z_k=-W_k(-1)$, $k\in\mathbb{Z}$. None of these is stable as $|f'(z_k)|>1$. The second auxilliary is $f^{(2)}(z)=z$ or $e^{e^z}=z$. This cannot be solved in terms of elementary functions, so you need to use Newton's method. Once you find a solution $z_0$, the fixed points will be $z_0$ and $f(z_0)$. You can test then for the period, by using the modulus of the derivative of the multiplier, as given by Shell, as $|(f^{(2)})'(z_0)|$. If that's less than one, then it will be a 2-cycle, with limits $z_0$ and $f(z_0)$.

In general you'll have to solve the $p$-th auxiliary $f^{(p)}(z)=z$, for which you can still use Newton's method, but as the composition becomes more and more entangled, it will progressively be slower and may even fail. If you get a point $z_0$, then all $\{z_0,f(z_0),f^{(2)}(z_0),\ldots,f^{(p-1)}(z_0)\}$ will be fixed points, which you can check using again the modulus of the multipler $|(f^{(p)})'(z_0)|$.

With that said, it's unknown really whether there are points of period $p$ for arbitrary $p$ in both tetration of the exponential and/or regular tetration. You can only check individual values. In one of my papers I extract the fixed points using functions which generalize $W$, but the check is still the same. They all have to go through Shell's multiplier to check for the modulus. You can get a rough idea on where to look, by graphing the iterates of the exponential like this.

Answer 3

update: an update on the Pari/GP routine, few textual improvements

I've got a sudden enlightenment which seems to solve the problem completely.

The key here is, that on one hand the fixed- and periodic points of $\exp(z)$ are all repelling (this was also mentioned/proved in an article of Shen/Rempe-Gillen, pg 1, see reference below), and on the other hand the one single fixed point of $\log(z)$ is nicely attracting, but it is only a singular occurence.

$1$-periodic points/fixed points

Well, further fixed points can be found by using branches of the $\log()$, say $$ \text{lb}(z,k) = \log(z) + k \cdot C \qquad \text{where } C = i 2 \pi$$ We may then have for some $p_1 = p_1' + C $ the equality $$ \exp(p_1) = p_1 = p_1' + C = \exp (p_1'+ C) $$ and on the other hand the inverse relation $$ \text{lb} (p_1,1) = p_1'+ C = \text{lb}(p_1'+C,1)$$

Noticing this we can exploit the attractive property of the (iterated) logarithmizing to converge from some initial value to the desired fixpoint, say from $z=1+I$ to some $p_1$ .

Example:

z = 1+I     | %681 = 1 + I
z=lb(z,1)   | %682 = 0.34657359 + 7.0685835*I
z=lb(z,1)   | %683 = 1.9568606 + 7.8049907*I
z=lb(z,1)   | %684 = 2.0852451 + 7.6083262*I
z=lb(z,1)   | %685 = 2.0654578 + 7.5864764*I

From where we can now use the Newton-iteration to get even quadratic convergence rate and then find the arbitrary well approximated value of the desired fixed point $\exp(z)=z$

z=newton(z) | %686 = 2.0622777 + 7.5886312*I
exp(z)-z    | %687 = 6.6538205 E-211 - 1.9010916 E-211*I

Using the $k$'th multiple of the constant $C=i2\pi$ we can now find (and index) the (infinitely many) complex fixed points ($1$-periodic): $$ p_1 = \text{lb}(p_1,k) \to \exp(p_1)=p_1$$ Another example:

p_1 = 1+I         | %688 = 1 + I
p_1=lb(p_1,3)     | %689 = 0.34657359 + 19.634954*I
p_1=lb(p_1,3)     | %690 = 2.9774671 + 20.402703*I
p_1=lb(p_1,3)     | %691 = 3.0262041 + 20.275440*I
p_1= newton(p_1)  | %692 = 3.0202397 + 20.272458*I
exp(p_1)-p_1      | %693 = 1.6045424 E-219 + 0.E-220*I  \\ error is machine- epsilon

2-periodic points

That procedere for finding $1$-periodic points is of course well known. For the finding of $1$-periodic (or: fixed-) points we have also the LambertW-function and their branching behaviour for even an immediate solution. But none such function is known for the $n$-periodic points for $n\ge 2$. Thus we have to find our own procedure now...

For that search of $2$-periodic fixpoints I'll not go to explain the formulae in detail (it is trivial but too tedious for this answer-box), but I simply state that for the search for a solution to $$ \exp(\exp(p_2) ) = p_2 \ne \exp(p_2) $$ it suffices to use -instead of the iterated exponential-function- the iterated branched logarithm-function, where the branch-index is allowed/required to change between the two steps of iteration:

$$ p_2 = \text{lb}( \text{lb}(p_2,k_0),k_1) $$

Initialize arbitrarily, iterate and, if desired, refine using the Newton-iteration on the $\exp(\exp())$ function.
Example:

p_2 = 1+I                | %694 = 1 + I
p_2=lb(lb(p_2,-1),0)     | %695 = 1.7063287 - 1.5078409*I
p_2=lb(lb(p_2,-1),0)     | %696 = 1.9537456 - 1.4538908*I
p_2=lb(lb(p_2,-1),0)     | %697 = 1.9430376 - 1.4429267*I
p_2= newton(p_2)         | %698 = 1.9428329 - 1.4437804*I
exp(exp(p_2))-p_2        | %699 = 6.1238446 E-202 - 1.6330252 E-201*I
exp(p_2)-p_2             | %700 = -1.0588348 - 5.4784957*I

We have now:

 p_2            | %701 = 1.9428329 - 1.4437804*I
 exp(p_2)       | %702 = 0.88399815 - 6.9222761*I
 exp(exp(p_2))  | %703 = 1.9428329 - 1.4437804*I

which is indeed a $2$-periodic point.

It is meaningful now, to simplify the notation for finding $2$-periodic points. Just let us use a vectorial notation for the two branch-indexes and write $$ p_2 = \text{Find}([k_1,k_2]) $$ implemented as Pari/GP-function (Pseudocode)

  Find(K) = my(z=1+I,k_1=K[1],k_2=K[2]);    \\ K is the vector [k_1,k_2]
     for(t=1,5,       \\ 5 or even only 3 iterations suffice to start Newton
           z=lb(z,k_1);
           z=lb(z,k_2);
         );
     return(Newton(z)) ;

Update A better routine, which also employs the Newton-iteration on the branched iterated logarithm (instead on iterated exponentiation):

 \\Pari/GP
 default(realprecision,200) \\ my usual numerical precision
 pi2i=2*Pi*I                \\ constant
 {Find(K,maxerr=1e-100,maxit=25,z0=1+I)=my(err,L,z,l_prod,n=#K);
    L=vector(n); \\ shall contain the sequence of logarithms/periodic points

    \\ the following preconditioning is likely not needed at all
    L[1]=z0; for(it=1,3,for(i=1,n,L[(i % n) + 1]=lb(L[i],K[i])));
    z0=L[1];

    \\ Newton-iteration on branched iterated logarithm,initial value z0
    for(it=1,maxit,
      z=z0;
      L[1] = l_prod = z;
      for(i=1,n,  L[(i % n)+1]=z=log(z)+K[i]*pi2i;  if(i<n,l_prod*=z) );
      err = (z-z0)/(1/l_prod-1); \\ denominator contains derivative
      z0 -= err;
      if(abs(err) < maxerr,break());
      );
    return(L);}

end update

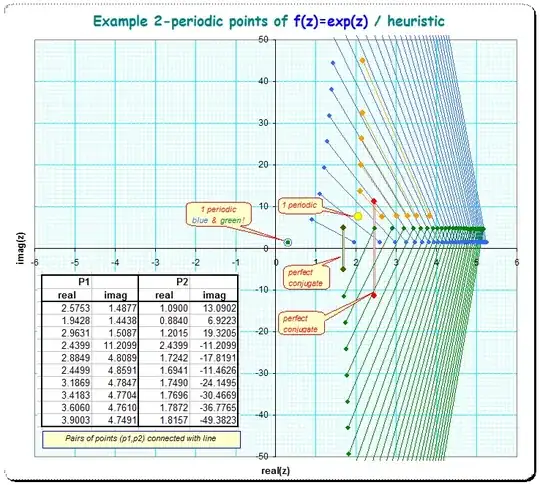
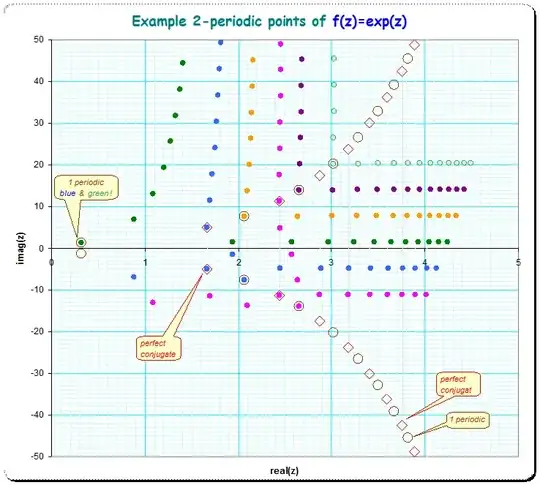
Using $Find([k_1,k_2])$ for $k_1=-3..3$ and $k_2=0..12$ I get the following chart of $1$- and $2$-periodic points (they are $1$-periodic when $k_1=k_2$) where the first parameter $k_1$ controls the color:

To see the $2$-periodicities, below is the same picture whith the pairs of periodic points connected by straight lines:

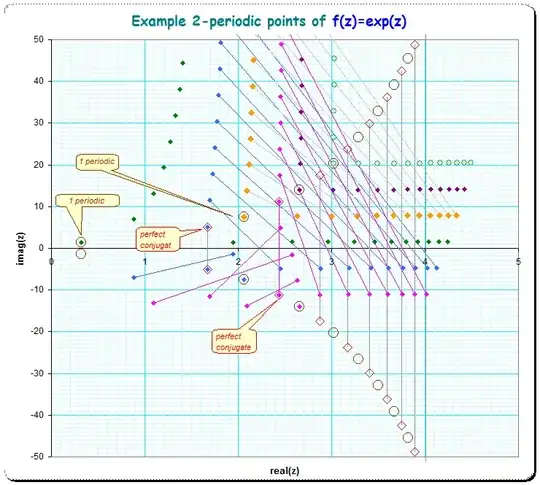
It is worth to note, that $2$-periodic points of the form $\text{Find}([k,-k])$ give pairs of complex conjugate numbers (big red diamonds), while $\text{Find}([k,k]) (=\text{Find}([k]))$ give $1$-periodic points (big brown circles). Note moreover that the $1$-periodic and the conjugate $2$-periodic points lay asymptotically on an (exponential) curve which can be seen, when the scale of the imaginary axis is taken as logarithmic (or even better transformed to $\sinh^{-1}()$ to see also the numbers with negative imaginary component ).

3-,4-,5-,... n-periodic points

If we extend the $\text{Find}([...])$ function to $3,4,5,...n$ entries $\in \mathbb Z$ in the vector-argument we find easily any $n$-periodic point which we like. $\text{Find}([0,0,1])$,$\text{Find}([0,0,-1])$,$\text{Find}([0,0,2])$,...$\text{Find}([0,1,1])$ ...

Finally $\text{Find}([k_1,k_2,k_3])$ with $k_1,k_2,k_3 \in \mathbb Z$ give all $3$-periodic points, and in case $k_1=k_2=k_3$ the $1$-periodic fixed points and in case $k_1=k_2=k_3=0$ the primary fixed point of the $\log()$-function. Unfortunately, as Y. Galidakis pointed out in his answer, the Newton-iteration for higher iterates of the $\exp()$ gets more&more involved; numerical checks up to $n=63$ and $20$ iterations in the $\text{Find}([...])$-function however looked very promising but are still under consideration.

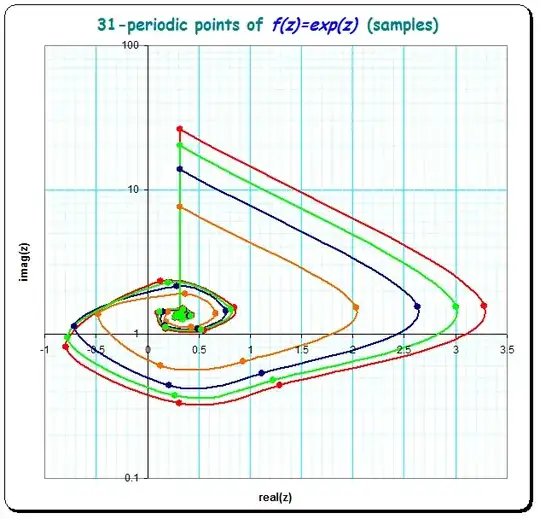
See here some picture for examples for $n=3$,$n=5$,$n=11$,$n=31$ - periodic points.

• $3$-periodic examples

Here the coloring is chosen to make the exemplars of one shape-family better discernible where one shape-family is meant as having chosen $k_1,k_2$ constant and only $k_3$ varying.

• $5$-periodic examples

• $13$-periodic examples

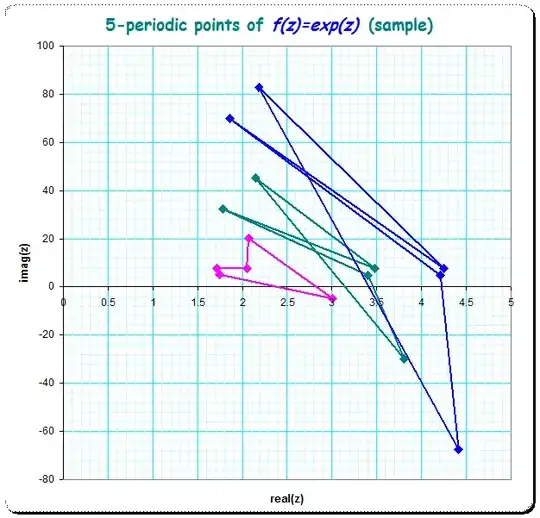
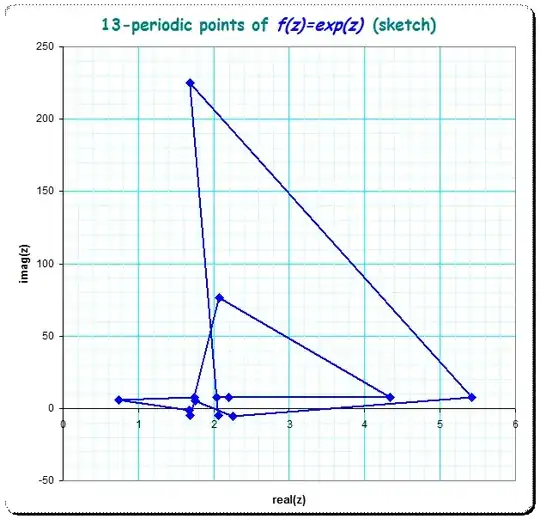
I have shown only one exemplar because the overlay of more exemplars of the shape-family makes the picture too chaotic

• $31$ - periodic example

Here I show 4 exemplars of a very special shape-family by keeping all but one of the vectorial arguments to zero: $$\text{Find}([0,0,...,0,k_{31}])$$ which produces the natural iteration-map for the $\log()$ for $30$ steps and then in one step adds $k_{31} \cdot C$ .
Of course, this typical shape-family exists analoguously for all $n$-periodic points.

Remark

This scheme, if it is really exhausting (what seems obvious to me), gives nice intuition in more general statements about the nature of the set-of-periodic points of the exponential function.

• The number of $2$-periodic fixpoints is then that of $\mathbb Z^2$. All of them can be indexed like the rational numbers by a pair of 2 integer indexes.

• The number of $n$-periodic fixpoints is then that of $\mathbb Z^n$. Indexing as before, but with $n$-tuple of integer indexes.

• If I understand the topological concept of "dense subset" correctly it is immediately obvious, that the set of $n$-periodic points is "dense" (Shen/Rempe-Gillen give a reference to a proof)

• Because there is so far no reason to assume that some class of $n$-periodic points might be missing/impossible, this answers one doubt in Galidakis' answer, by here claiming that $n$-periodic point for all $n$ exist and there are $\mathbb Z^n$ of them.(See also Shen/Rempe-Gillen, Theorem 1.1)

• I don't know yet, whether it shall be possible to find, for instance for the $2$-periodic points, a simpler analytical description than this of the iterated branched logarithms, for instance by a parametrical definition of the curves on which that points lay, for instance to prove the exhaustiveness of my method for the set of 2-periodic orbits/points.

Shen, Zhaiming; Rempe-Gillen, Lasse, The exponential map is chaotic: an invitation to transcendental dynamics, Am. Math. Mon. 122, No. 10, 919-940 (2015). ZBL1361.37002.

Update: an article which deals with the question of $p_1$ (fixed-) points on the braches of the $\log()$-function is by Stanislav Sykora (2016) at his web-space here . Don't know really whether the exposition can be used at least as proof for the questions whether the set of fixed points $p_1$ found by this method here is really exhaustive, though.

Answer 4

At question 2 and 3:

I didn't find any 2-periodic points where (at least) one has negative sign on the real part.

It seems that the few cases with negative real parts are not helpful/powerful enough to base a Cesaro-summation of the infinite series on the n-periods of the periodic points.

---

The following are periods found by random-generating vectors of $K$ (values $-10...10$, periods as documented. For each period length 2000 tries. Nothing systematic so far!

 period:5
 [0, 0, -5, 6, 0]
 3.59082749599 + 1.47618971232*I
 1.35645844221 + 0.390038693480*I
 0.344597110913 + 0.279988561156*I
 -0.811918635625 - 30.7336040230*I
 3.42570548172 + 36.1019037153*I


 period:5
 [0, -3, 7, 0, 0]
 1.39589550907 + 0.381166300943*I
 0.369493169111 + 0.266563764150*I
 -0.786115761464 - 18.2245911795*I
 2.90370129081 + 42.3683926548*I
 3.74874562619 + 1.50236871704*I

6

 period:6
 [0, 0, 5, 0, -2, 0]
 2.50151898932 - 1.46197427832*I
 1.06381612289 - 0.528895733527*I
 0.172303614637 - 0.461379744497*I
 -0.708253491774 + 30.2025438493*I
 3.40820103291 + 1.59424215683*I
 1.32512022296 - 12.1288407143*I


 period:6
 [-10, -2, 0, 0, 0, 0]
 -0.865726055159 - 1.16777496158*I
 0.374096952332 - 65.0405893212*I
 4.17502806712 - 14.1314152585*I
 2.69024296013 - 1.28352546925*I
 1.09217349774 - 0.445163548252*I
 0.165016321238 - 0.387035882053*I


 period:6
 [6, 0, 0, 0, 1, -5]
 1.94758289292 - 29.7291698287*I
 3.39426995654 + 36.1937328801*I
 3.59326415488 + 1.47728921312*I
 1.35714636151 + 0.390061973605*I
 0.345069979151 + 0.279869780194*I
 -0.811260602392 + 6.96462918257*I

7

 period:7
 [-3, -4, 9, 0, 0, 0, -1]
 -0.750444308081 - 5.74329299488*I
 1.75649728498 - 20.5502806192*I
 3.02651414772 - 26.6182716405*I
 3.28802037436 + 55.0910858620*I
 4.01076580829 + 1.51118369513*I
 1.45535723212 + 0.360331909844*I
 0.404999059491 + 0.242709153027*I


 period:7
 [-8, 5, -7, 1, 0, 0, 6]
 -0.170370792911 + 38.2832303265*I
 3.64502185218 - 48.6902358879*I
 3.88827281086 + 29.9198522843*I
 3.40689602021 - 42.5407328375*I
 3.75365864051 + 4.79230392555*I
 1.80621689648 + 0.906341375286*I
 0.703523044147 + 0.465078494459*I

8

 period:8
 [9, 2, 6, -10, 1, 0, 0, 4]
 -0.183435398095 + 25.6847041258*I
 3.24592114662 + 58.1266057847*I
 4.06418024304 + 14.0813826162*I
 2.68486042576 + 38.9889234027*I
 3.66564298323 - 61.3298103386*I
 4.11804903195 + 4.77208731106*I
 1.84106769616 + 0.858834846465*I
 0.708790828907 + 0.436479925461*I


 period:8
 [0, 6, 2, 8, 3, -2, 0, 0]
 1.02121461182 - 0.489741421848*I
 0.124493728473 - 0.447168470622*I
 -0.767493877253 + 36.3998441297*I
 3.59478673353 + 14.1582489042*I
 2.68153380067 + 51.5876324277*I
 3.94463110922 + 20.3684188203*I
 3.03239537454 - 11.1868702610*I
 2.45019248787 - 1.30608992453*I


 period:8
 [7, 4, 4, -4, 1, 0, 0, 2]
 -0.139550493338 + 13.1980686114*I
 2.58012639847 + 45.5636666372*I
 3.82071134899 + 26.6469711272*I
 3.29285053446 + 26.5611256149*I
 3.28707484580 - 23.6852881281*I
 3.17439265913 + 4.85028944014*I
 1.75729393145 + 0.991281741545*I
 0.701910122418 + 0.513600707428*I

10

 period:10
 [13, 11, 0, 0, 0, -1, -2, 7, -8, -6]
 3.88980667763 - 39.1931011362*I
 3.67340164853 + 80.2095359456*I
 4.38569002022 + 70.6400691168*I
 4.25952110464 + 1.50879089393*I
 1.50825667185 + 0.340425849316*I
 0.435798949967 + 0.221988383926*I
 -0.715228532737 - 5.81205985617*I
 1.76745009101 - 14.2596107258*I
 2.66505425965 + 42.5348198592*I
 3.75228206472 - 48.7572601585*I


 period:10     range for entries of K is -20 to +20
 [13, 0, 0, 0, 9, -14, -4, 7, -2, -5]
 2.45890496064 - 32.6598313838*I
 3.48897209063 + 80.1857592496*I
 4.38529164743 + 1.52731263559*I
 1.53550026359 + 0.335142367490*I
 0.452125566132 + 0.214892564673*I
 -0.691955916993 + 56.9923559438*I
 4.04299085160 - 86.3816573645*I
 4.45986945473 - 26.6567678748*I
 3.29684662012 + 42.5772726672*I
 3.75430951723 - 11.0728521642*I

31

 period:31    range for entries of K is -50 to +50
 [18, 41, 5, 3, -43, -44, 35, 7, -2, 46, 32, -39, 22, 0, -49, 7, 44, 19, 17, -36, 0, 0, 0, -10, -6, 32, 12, 33, -43, 14, -43]
 4.46123659082 - 268.670811286*I
 5.59362472174 + 111.543142519*I
 4.71566725871 + 259.131288260*I
 5.55750039366 + 32.9685268863*I
 3.50956315667 + 20.2533523759*I
 3.02311284853 - 268.777751156*I
 5.59394808482 - 278.019702686*I
 5.62789436426 + 218.360807399*I
 5.38648079756 + 45.5273258094*I
 3.82526317868 - 11.1133399676*I
 2.46413008062 + 287.787230418*I
 5.66225807926 + 202.624164033*I
 5.31174315327 - 243.501368016*I
 5.49536042974 + 136.681090990*I
 4.91845800632 + 1.53061225907*I
 1.63921352217 - 307.574382164*I
 5.72873115272 + 42.4168302595*I
 3.75658336920 + 277.896704179*I
 5.62734083557 + 120.937800074*I
 4.79635775505 + 108.338449219*I
 4.68623916110 - 224.668117822*I
 5.41484177250 - 1.54994085447*I
 1.72851827511 - 0.278785039562*I
 0.560104777428 - 0.159908482226*I
 -0.540452863018 - 63.1099522429*I
 4.14491514575 - 39.2784716315*I
 3.67621370882 + 199.596270778*I
 5.29646626740 + 76.9506038467*I
 4.34552685950 + 208.847190418*I
 5.34181926132 - 268.626976088*I
 5.59352139149 + 86.4136809929*I

The values for the elements of the periods can be approximated to arbitrary precision, when Newton-iteration on the iterated branched logarithm is applied.