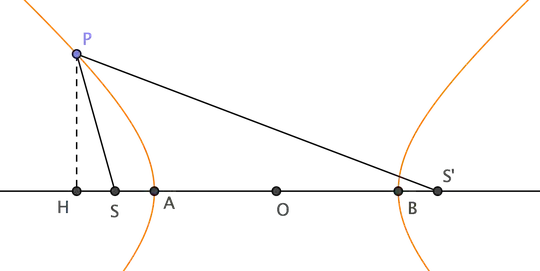
Let $S$, $S'$ be the foci of the hyperbola, $P$ a point on it and $H$ the projection of $P$ on line $SS'$ (see figure below). I'll suppose WLOG that $S$ is the focus nearest to $P$ and that $\angle PSS'>90°$; the reasoning must be slightly rephrased if $\angle PSS'\le90°$ but the same conclusions still hold.
By the Pythagorean theorem we have:
$$
PH^2=PS^2-HS^2=PS'^2-HS'^2,
$$
that is:
$$
(PS'-PS)(PS'+PS)=(HS'-HS)(HS'+HS).
$$
Observe that $HS'-HS=SS'=2c$ (here we define constant $c$ as usual) and $HS'+HS=2OH$, while by hypothesis: $PS'-PS=AB=2a$ (here we define constant $a$ as usual). Plugging these equalities into the above formula we get:
$$
\tag{1}
PS'+PS={2c\over a}OH.
$$
We can then compute the area of triangle $PSS'$ in two ways: either considering $SS'$ as base and $PH$ as the related altitude, or by Heron's formula. Equating the resulting expressions and squaring, we then obtain:
$$
(c\cdot PH)^2={1\over16}(PS+PS'+2c)(PS+PS'-2c)(-2a+2c)(2a+2c),
$$
that is:
$$
c^2PH^2={1\over4}\big((PS+PS')^2-4c^2\big)(c^2-a^2).
$$
If we now introduce, as usual, the constant $b^2=c^2-a^2$, this gives:
$$
\tag{2}
(PS+PS')^2=4c^2\left({PH^2\over b^2}+1\right)
$$
We can then combine equations $(1)$ and $(2)$ to eliminate $PS+PS'$ and finally get:
$$
{OH^2\over a^2}={PH^2\over b^2}+1,
$$
which is the cartesian equation of the hyperbola, once you set $x^2=OH^2$ and $y^2=PH^2$.
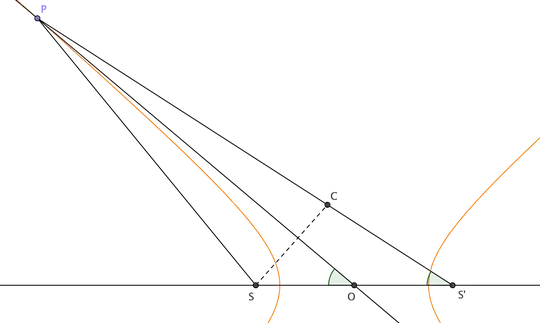
To understand geometrically the origin of asymptotes, consider the case when point $P$ is very far from the center: $OP\gg c$. Choose point $C$ on $PS'$ such that $PC=PS$ and consequently $CS'=2a$ (see figure below). Angles at $S$ and $C$ in isosceles triangle $PSC$ get nearer and nearer to $90°$ the farther $P$ is, while line $OP$ intersects the hyperbola at $P$ and $P'$, the symmetric of $P$ with respect to $O$.
In the limit $OP\to\infty$ lines $SP$, $OP$ and $S'P$ become parallel and triangle $SCS'$ becomes right-angled. The angle $\alpha$ line $OP$ forms with $SS'$ tends to a constant value such that $\cos\alpha=a/c$, and line $OP$ is tangent to the hyperbola "at infinity", i.e. it is an asymptote.