1

Suppose two circles($C_1,C_2$) touch each other externally. How many different circles($C$) can be drawn such that these two circles touch it internally?

I made a quick rough sketch of how it looks:

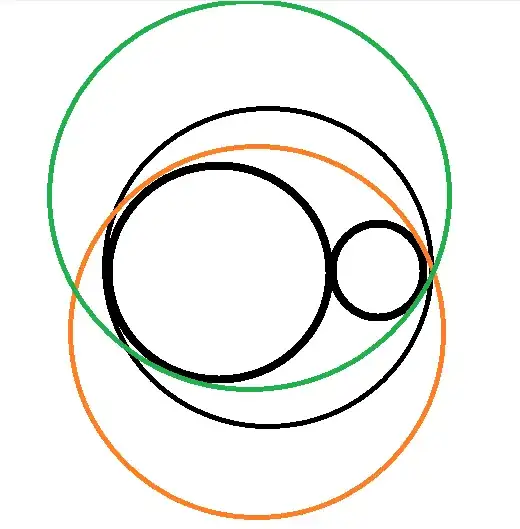
The thick black inner circles are $C_1,C_2$ and the thinner black, red and green circles are possible $C$s

It seems like I can draw an infinite number of circles $C$ satisfying the condition. Am I right in saying so?

If yes, is there a relationship between the radii of $C$s?

Also, are there any texts or sources that talk about this?

DatBoi
  • 4,055

2 Answers2

3

If $O$ is the center of a circle of radius $R$ tangent to the circles $C(O_1, R_1)$, $C(O_2, R_2)$ then we have $$OO_i = R- R_i$$ $i=1,2$, and so $$OO_1 - OO_2= R_2 - R_1$$

Conversely, if $OO_1 - OO_2= R_2 - R_1$, then take $R = OO_i + R_i$, $i=1,2$. Note that such points $0$ exist ( infinitely many) as long as $|R_2 - R_1| < O_1 O_2$, that is, as long as the two initial circles are not one containing the other.

orangeskid
  • 53,909
1

Suppose that

  • circle $C_1$ has radius $r_1$ and is centered at the point $P_1$
  • circle $C_2$ has radius $r_2$ and is centered at the point $P_2$.

Let the center of the outer tangent circle be at the point $P=(x,y)$.

Then, as the other answer demonstrates $$ dist(P,P_1) - dist(P,P_2) = r_1 - r_2 $$ This immediately shows that the guess I made in my comment is correct: in fact $P$ lies on (one branch of) a hyperbola with foci at $P_1$ and $P_2$.

If you want to know the equation of the hyperbola and it’s asymptotes, that’s all worked out very nicely in the answer to this question.

The algebra will work out more cleanly if you work in a coordinate system where $P_1 = (-a,0)$ and $P_2= (a,0)$.

bubba
  • 43,483
  • 3
  • 61
  • 122