We have Comparing $\pi^e$ and $e^\pi$ without calculating them but it doesn't give an approximation of the actual difference. Is there a way without calcualting an approximation of them to prove $e^\pi - \pi^e < 1$ ?
Asked
Active
Viewed 315 times
6
-
6We can still follow some of the proofs there to conclude $e^{\pi}<1+\pi^e$. Did you try this? – Dietrich Burde Feb 24 '20 at 19:41
-
Could you link the one that works for this? I must have missed something obvious. – chx Feb 24 '20 at 20:13
-
The difference is small, the task won't be easy. – Feb 24 '20 at 21:10
-
1Like this? – rtybase Feb 24 '20 at 21:29
1 Answers
0
If that can help:
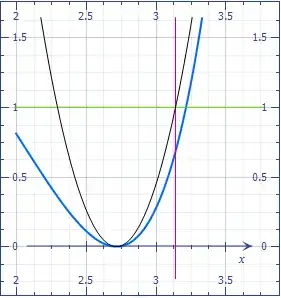
Let $f(x):=e^x-x^e$. This function has a minimum at $x=e$ (double root), and the second order Taylor development is
$$y\approx g(x):=e^{e-1}(x-e)^2.$$
This approximation exceeds $f$, but we still have $g(\pi)<1$.
In blue, $f$, in black, $g$.
-
Hard to see definitely that the black curve is less than $1$ at $x=\pi$ from this plot. – mjw Feb 24 '20 at 21:54
-
Oh, you want the blue plot less than 1. That is pretty clear, but then you wouldn't need the Taylor series. – mjw Feb 24 '20 at 21:55