How is Laplace transform more efficient?

Question

I wrote an answer on Laplace Transform, following a series of lectures by Prof.Ali Hajimiri (kindly take a look at the answer, my question is entirely based on that answer). In this answer, though I was able to arrive at the Laplace transform with operational calculus, I had a hard time figuring out what "applying Laplace Transform on both sides" meant, from the standpoint of this answer.

I mapped out the steps involved in solving a differential equation, $y'(t)=x(t)$ with the operator-method and using the Laplace transform.

Operator Method

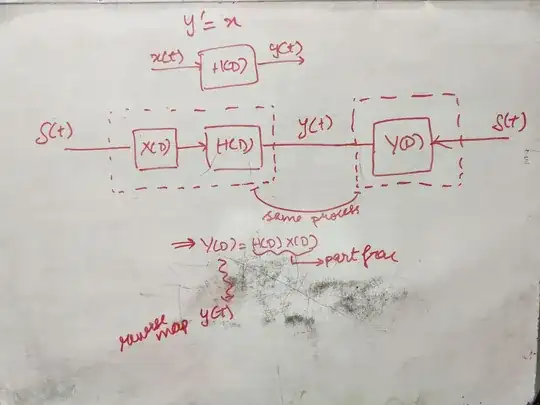
The Operator method: Assuming the inputs $x(t)$ and $y(t)$ are the impulse responses of a system with system operators $X(D)$ and $Y(D)$, will imply, $Y(D)=H(D)X(D)$, and then we can find $y(t)$ by reverse mapping. So a convolution in time domain $y(t)=h(t) * x(t)$ ($h(t)$ is the impulse response of the system) becomes multiplication in "operator" domain $Y(D)=H(D)X(D)$

Using Laplace Transform

Laplace Transform method: While taking laplace transform on both sides of a differential equation,$y'(t)=x(t)$ in this example, we are assuming y(t), is the impulse response of a system say sys1 and x(t) is the impulse response of another system say sys2. $Y(D)$ be the system operator of sys1. Now we need $y'(t)$, so the system operator becomes $DY(D)$ to produce $y'(t)$. And $X(D)$ be the system operator of sys2. Since $y'=x$ the two machines $DY(D)$ and $X(D)$ must be the same. Now if we give an input $e^{st}$ to sys1 and sys2, we know the system operator for sys1 becomes $sY(s)$ and for sys2 it's $X(s)$. Now as these two systems are equal, $sY(s)=X(s)$ which implies that $Y(s)=\dfrac{X(s)}{s}$. Now reverse map $Y(s)$ to obtain $y(t)$.

Is my interpretation correct?

As far as I can see, Laplace transform has just complicated things. How does it simplify the process. Why do we use Laplace transform? I understand that this question is highly specific. But if someone can help, it would be highly helpful. Thanks in advance.

Example:

Consider a differential equation, $y'' + 3y' + 2y = e^{-3t}u(t)$, with zero initial conditions, where $y$ is function of $t$ and $u(t)$ is the step function,

$i)$ Operator Method:

$$(D^2+3D + 2)y = e^{-3t}u(t)$$ $$y=\left( \dfrac{1}{D^2+3D + 2}\right) e^{-3t}u(t)$$ Expressing $y$ and $e^{-3t}$ in terms of $\delta(t)$ $$Y(D)\delta(t) = \left( \dfrac{1}{D^2+3D + 2}\right) \left( \dfrac{1}{D+3} \right) \delta(x)$$ $$\implies Y(D) = \dfrac{1}{(D+1)(D+2)(D+3)}$$ $$Y(D) = \dfrac{1/2}{D+1} - \dfrac{1}{D+2}+\dfrac{1/2}{D+3} \tag*{...(1)}$$ Reverse mapping, $$y(t)= \left(\dfrac{e^{-t}}{2} - e^{-2t} + \dfrac{e^{-3t}}{2}\right)u(t)$$

$ii)$ Using Laplace transform:

Taking Laplace transform on both sides, $$s^2Y(s) + 3sY(s) + 2Y(s) = \dfrac{1}{s+3}$$ $$Y(s) = \dfrac{1/2}{s+1} - \dfrac{1}{s+2}+\dfrac{1/2}{s+3}$$ We could've replaced $D$ by $s$, in $(1)$ since the input is of the form $e^{st}$

Now, taking inverse Laplace transform on both sides, $$y(t)= \left(\dfrac{e^{-t}}{2} - e^{-2t} + \dfrac{e^{-3t}}{2}\right)u(t)$$

Note, if the input contained any of the natural frequencies ($e^-t$ or $e^-2t$), we can't use the Laplace transform to obtain the response, but we can still use the operator method. And we can obtain only the forced response with the Laplace, but the operator method also gives us the natural repsonse. Which again leads me to the question, why is Laplace transform more efficient?

---

In-short, give me an example where, an ODE is unsolvable with the operator-method, but becomes a piece of cake with the Laplace transform.

I don't exactly intend to prove that the operator method is superior or something, but I want to know why Laplace is preferred over the operators? In what way, does that work around simplify the journey? When I look at it, we actually need not even take Laplace on both sides to get H(s) we just have to find H(D) and replace D by s, which seems to be relatively easy, isn't it?

Edit:

Following are the thing(s), I could see,

1. When we use Laplace transform, we have a way to analyse the system's response to various frequencies, just by looking at the transfer function(D replaced by s in system function), as it's a function of input frequency $s$. That's the only advantage as far as I can see, but I guess I'm not experienced enough to appreciate its significance.

2. The function $e^{st}$ is an Eigen function for the differential operator and the Laplace Transform performs a change of basis in disguise. I don't know how to relate this linear algebra interpretation to this map of operations. Does this mapping of the operations shed some light on how the change of basis takes place, or is it completely unrelated(it can't be)?

   ---

Someone shared a link, Operator Calculus. That article really gave some insight as to why Laplace overtook Operators, from an historical perspective. Primarily because(as far as I can see) Heaviside really thought it was contemptuous to "prove" his methods.

But is there no mathematical convenience at all?

---

Sub-question: What actually allows us to use the operator like a variable?

---

Specifics on operator-method:

1. What is the operator method?

2. How to handle time delays?

3. How to handle initial conditions?

Answer 1

Firstly, you say that with Laplace transform we can only calculate forced response. I think one can also find the initial condition response with Laplace transform with the formula:

\begin{equation*} L{(\frac{d^n}{dt^n}y(t))}=s^nY(s)-s^{n-1}y(0)-s^{n-2}y'(0)-\cdots -sy^{(n-2)}(0) -y^{(n-1)}(0) \end{equation*}

Secondly, you say that if input contains natural frequencies then Laplace transform fails. I read your answer about Laplace transform, but there you derive general formula by assuming the input frequency is not equal to one of the natural frequencies of the system. In fact, in your formula there you have $H(s_0)$, which is infinity at poles. However, I think, it is that formula that fails, not the Laplace transform. For example, consider your system in this question and input $e^{-2t}$. Then we have:

\begin{equation*} Y(s)=H(s)U(s)=\frac{1}{s^2+3s+2} \frac{1}{s+2}= \frac{1}{(s+2)^2(s+1)} \end{equation*}

Then you can find $y(t)$ as

\begin{equation*} y(t) = L^{-1}(Y(s))= L^{-1}\left(\frac{1}{(s+2)^2(s+1)}\right) = L^{-1}\left(\frac{-1}{(s+2)^2}+\frac{-1}{s+2} + \frac{1}{s+1}\right) \\ = -te^{-2t}-e^{-2t}+e^{-t}. \end{equation*}

Finally, why we prefer Laplace transform? At least in my opinion, Laplace transform is well defined, but operator domain seems little bit more abstract. For example what is the meaning of D in your equations? I think it is a bit abstract. However, Laplace transform is well defined as:

$L(y(t))=\int_0^\infty y(t)e^{-st}dt$

and all the properties follow from the definition. So you straightforwardly understand what is $s$ standing for in the equations.

Any objections or corrections are welcome.