0

I wrote an answer on Laplace Transform, following a series of lectures by Prof.Ali Hajimiri (kindly take a look at the answer, my question is entirely based on that answer). In this answer, though I was able to arrive at the Laplace transform with operational calculus, I had a hard time figuring out what "applying Laplace Transform on both sides" meant, from the standpoint of this answer.

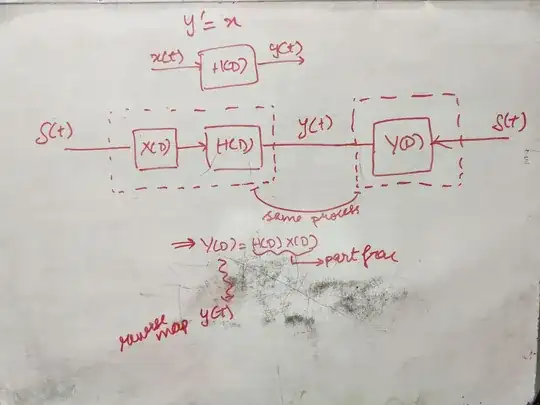
I mapped out the steps involved in solving a differential equation, $y'(t)=x(t)$ with the operator-method and using the Laplace transform.

Operator Method Operator Mehtod

Using Laplace Transform enter image description here

Laplace Transform method: While taking laplace transform on both sides of a differential equation, y'(t)=x(t) in this example, we are assuming y(t), is the impulse response of a system say sys1 and x(t) is the impulse response of another system say sys2. Y(D) be the system operator of sys1. Now we need y'(t), so the system operator becomes DY(D) to produce y'(t). And X(D) be the system operator of sys2. Since y'=x the two machines DY(D) adn X(D) must be the same. Now if we give an input $e^{st}$ to sys1 and sys2, we know the system operator for sys1 becomes sY(s) and for sys2 it's X(s). Now as these two systems are equal, sY(s)=X(s) which implies that Y(s)=X(s)/s. Now reverse map Y(s) to obtain y(t).

Is my interpretation correct?

As far as I can see, Laplace transform has just complicated things. How does it simplify the process. Why do we use Laplace transform? I understand that this question is highly specific. But if someone can help, it would be highly helpful. Thanks in advance.

Aravindh Vasu
  • 599
  • Hmm I believe this question should be asked in math stack exchange. –  Nov 11 '19 at 14:57
  • Did you actually try it on a real equation? The answer you wrote on Math Stack Exchange hasd a step where you go "Now, looking at (1)&(2) it's evident that" which will almost never be the case. – DKNguyen Nov 11 '19 at 15:24
  • @DKNguyen Sorry I don't understand what you mean? – Aravindh Vasu Nov 11 '19 at 15:24
  • @AravindhVasu All your examples don't seem to show you working with a real ODE, just models of one. – DKNguyen Nov 11 '19 at 15:26
  • @DKNguyen Please, checkout my answer on math stack – Aravindh Vasu Nov 11 '19 at 15:27
  • I already did when I responded – DKNguyen Nov 11 '19 at 15:27
  • @DKNguyen So you want me to add some examples? – Aravindh Vasu Nov 11 '19 at 15:28
  • I don't really need examples, but all the examples you show are simple models of ODEs that are tailored so you can solve them without Laplace. It's not difficult to run into one where you suddenly can't. (or takes more work). At least, that's what I remember thinking the last time I had to work with this stuff because I used to prefer it to solve it the way you did too, until I ran into one where I could not. – DKNguyen Nov 11 '19 at 15:30
  • oh, mathjax on this site is $. It's not like the other stack exchange sites. – DKNguyen Nov 11 '19 at 15:34
  • @DKNguyen "Now, looking at (1)&(2) it's evident that" which will almost never be the case." It does work, because, any higher order polynomials can be broken down into first or second order polynomials(if you avoid complex roots) according to the fundamental theorem of algebra. Therefore that result is sufficient. – Aravindh Vasu Nov 11 '19 at 15:38
  • I think you just haven't run into the right problems yet. Kind of like asking what's the point of matrices when you can just solve simultaneous equations by rearranging and substituting them into each other. – DKNguyen Nov 11 '19 at 15:54
  • @DKNguyen Maybe, but all my arguments are based on the course taken by the caltech prof Ali Hajimiri – Aravindh Vasu Nov 11 '19 at 15:56
  • Have you considered PDEs yet? – DKNguyen Nov 11 '19 at 16:01
  • @DKNguyen No, but sure there's got to be operational calculus for PDEs. I honestly don't get your point. In the same link, https://math.stackexchange.com/a/2019815/525644 this answer is also based on operational calculus and is much more rigorous compared to mine. – Aravindh Vasu Nov 11 '19 at 16:12
  • @Rahul Ah yes, I actually posted the same question in two different sites, but this was migrated here. – Aravindh Vasu Nov 26 '19 at 12:56

0 Answers0