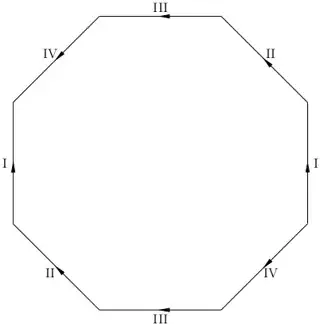
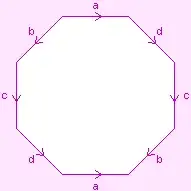
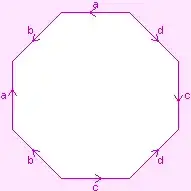
There are four octagon gluing patterns (up to rotation and relabelling) which give a double torus. Starting with the two that you have depicted, here they all are:
- a b c d A B C D
- a b A B c d C D
- a b A c B d C D
- a b c A B d C D
To convert these into pictures, start from one corner of the octagon and walk around it in the counterclockwise direction. When you see lower case, write that letter and a counterclockwise arrow. When you see upper case, write the lower case letter and a clockwise arrow.
What distinguishes these patterns is that all 8 corners are identified to give $V=1$ point. The 8 sides are identified in pairs to give $E=4$ edges, and of course there is $F=1$ face. The Euler characteristic formula gives
$$\chi = V-E=F = 1 - 4 + 1 = -2
$$
For an oriented surface of genus $g$ --- the double torus has $g=2$ --- one has $\chi = 2-2g$. So all together we get $-2=2-2g \implies g=2$, as expected.
Other (oriented surface) octagon gluing patterns will identify the 8 corners into either 3 or 5 points, as it turns out, with (respective) Euler characteristics $\chi = 0$ or $2$, giving the surface of genus $1$ which is the torus), or of genus $0$ which is the sphere).
Rigorous proofs of all these relations between Euler characteristic and genus can be found in any treatment of the Classification of Surfaces. The other statements here, regarding octagon gluing patterns, are proved by simply enumerating combinatorial possibilities.