Let's say we draw a bicubic graph $G_{6/8}$ on a genus $2$ surface, i.e. $g=2$, which is a double torus. Euler's formula then reads: $$ F+V=E+(2-2g)=E-2, $$ where $F=\sum f_k$, the number of $k$-gons. Now, let's restrict $G_{6/8}$ to $f_6$ hexagons and $f_8$ octagons only. Since its $3$-regularity it follows that: $$ \sum_k (2d-k(d-2))f_k=2d\chi \underbrace \Longrightarrow_{ \begin{array}{lcr} d&=&3\\ k&\in&\{6,8\}\\ \chi&=&-2 \end{array} } 0\cdot f_6 -2 \cdot f_8=-12, $$ means we have $6$ octagons next to hexagons. See here for an example graph...
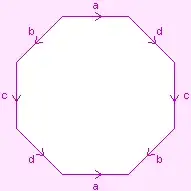
Having no double torus at hand, we draw the graph in the fundamental polygon related to the double torus:
My question:
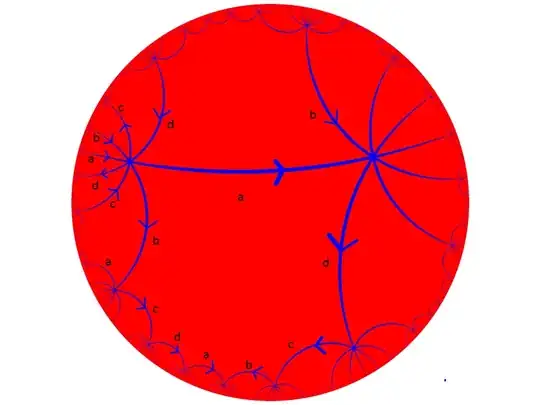
If we extend the fundamental polygon to the order-8 octagonal tiling of the hyperbolic plane and label the edges accordingly, i.e.
wouldn't we get a semi-regular tiling from any such graph $G_{6/8}$?