3

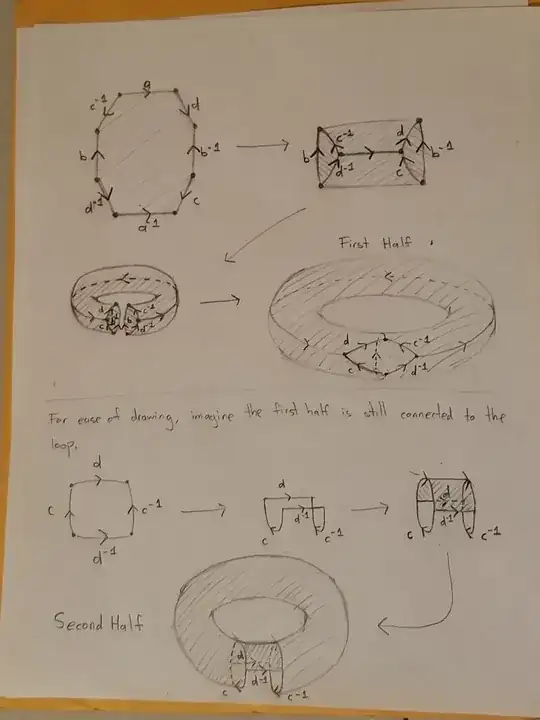
There are at least two ways of gluing an octagon to form a double torus. One is displayed in this YT video. There is another way by identifying opposite sides. Here is an image detailing the process.

Now, this construction is intrinsically different from the one linked in the video. The $cd^{-1}c^{-1}d$ path in the image is a loop the is homologous to zero, yet not null-homotopic. This is not true for the two pairs of opposite sides in the video.

A sequence of edges on the fundamental polygon can correspond to a loop on the resulting surface. For example, in the image, $adc^{-1}$ corresponds to a loop going around a hole in the double torus.

It is my suspicion that these loops generate the homotopy group, minus the trivial loop.

So, I ask: Do the homotopy and homology group generators of the quotient space uniquely correspond to edges of the fundamental polygon and the attaching word? Can you uniquely determine the generators given an octagon and the needed letters?

In the example above, the same edges correspond to different generators(Although in the end, the generators are all the same, generating the same homotopy and homology groups).

EDIT: I would also be glad to know if this holds true specifically for the torus or double torus. Additionally, if we are given the order of the gluing(a to b to c...), is it now guaranteed to be unique?

1 Answers1

1

Some of your questions strike me as mildly ill-posed, so please help clarify if my answer does not help.

As far as the fundamental group: yes, given a CW complex—the examples you give, for instance, you can always calculate a presentation for the fundamental group as follows. Write $X$ for the CW complex and $X^1$ for its $1$-skeleton (the edges). Mainly for convenience, let's assume the $1$-skeleton of $X$ is connected; in any case it is a graph. Collapsing a maximal tree in the $1$-skeleton yields an identification with the free group—that is, the generators of the fundamental group correspond in more or less the way you observed, to the loops in the $1$-skeleton.

Now, whenever we glue in a $2$-cell, the effect is that of making the loop (or word in the generators) nullhomotopic, and thus trivial in the fundamental group. It is a theorem (see Chapter 1 of Hatcher's Algebraic Topology for basically all of this) that adding higher-dimensional cells does not change the fundamental group.

Actually, going the other way is possible to! To every finite presentation, you can follow this process to build a $2$-complex with fundamental group equal to the group given by that presentation. (I believe this is an exercise in Hatcher's Chapter 1.)

Groups typically have many generating sets and many presentations, so it's not clear how the groups and the spaces match up. In fact, in general it is not algorithmically decidable whether a given finite presentation actually presents the trivial group!

As for homology, maybe you know already that the first homology group of a space (with integral coefficients) is just the abelianization of its fundamental group. Generators of the fundamental group therefore generate (as cycles, not loops) the abelianization, but typically there may be some redundancy in this generating set.

Finally, for higher homotopy groups, this perspective seems to somewhat break down: the $n$th homotopy group of a CW complex is determined by the $n+1$-skeleton, but e.g. spheres have somewhat strange higher homotopy groups that do not appear to me to arise naturally from the description of a sphere as a CW complex. For higher homology groups, there is cellular homology, which does succeed in continuing in this vein, with the downside that it becomes more challenging to do explicit computation once you lose cyclic ordering.

Just to finish by coming back down to earth some, yes, there are many fundamental polygons for the double torus. the one with word $aba^{-1}b^{-1}cdc^{-1}d^{-1}$ highlights the fact that the double torus is the connect-sum of two tori. Others may express another feature of the double torus, such as realizing it as a translation surface.

Rylee Lyman
  • 3,930
  • +1, great answer, but what do you mean by: "first homology group of a space (with integral coefficients)"? By space you mean $X$(?), but what about "integer coefficients"? Of what? Thanks... – draks ... Sep 06 '19 at 08:10
  • This was a response to a part of this OP's question that was not contained in your question. Given a space $X$ and a module $M$, there are homology groups $H_\ast(X,M)$. The ones people usually meet first have $M=\mathbb Z$; this is sometimes called homology with integer coefficients. – Rylee Lyman Sep 06 '19 at 11:17
  • In case this is a new concept to you: if you think about the fundamental group as maps of $S^1$ into $X$ that are trivial when the image can be extended to a map from the disc $D^2\to X$, homology (loosely), the same except maps are now trivial when they can be extended to a map from a $2$-manifold with boundary $M^2\to X$ – Rylee Lyman Sep 06 '19 at 11:20
  • You say: "As far as the fundamental group: yes". Would you mind pointing out the difference between the two ways to construct the double torus here? – draks ... Sep 06 '19 at 20:34