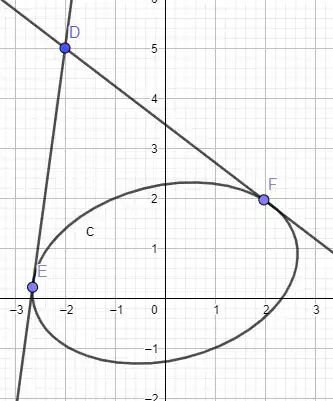
I am trying to obtain the two tangent lines to an ellipse passing through a certain point. I found some similar questions but none that I could find used the ellipse equation $Ax^2 + Bxy + Cy^2 + Dx + Ey + F$.
Looking at the below example, I want to obtain the two points E and F where the ellipse and the point D are known. How am I able to calculate those tangent lines (or points) for a rotated ellipse?