-1

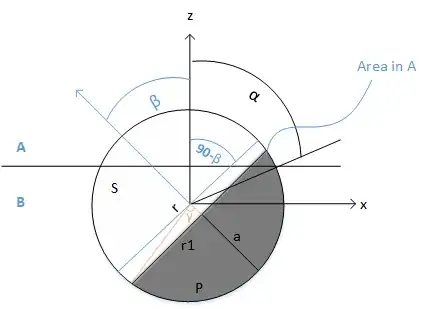
I have a sphere with radius $r$ that equally divided in to two hemisphere P and S. There is a plane that separate two different zone A and B. Upper zone called A and lower zone called B. $\alpha$ is the contact angle. So $\alpha $ larger means sphere is more in zone A and vice versa. Range of $\alpha $ can go between $[0,\pi]$The angle $\beta$ defines the orientation of the sphere which is an angle between z axis (vertical) and a unit vector. Range of $\beta $ can be $[0,2\pi]$. The Schematic representation of this is below.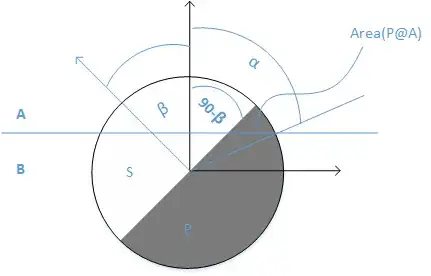enter image description here

To calculate the area of $P$ portion of the sphere into $A$ is given by following equation $$ \mathrm{Area}_{P@A}= r^2\int_{\theta=\frac{\pi}{2}-\beta}^\alpha \int_{\phi=\arcsin(1/(\tan\theta \tan \beta))} ^{\pi -\arcsin(1/(\tan\theta \tan \beta)} \sin\theta\; d\theta d\phi. $$

After solving this equation we can get the following solution. $$ \textrm{Area}_{P@A}= 2 r^2 \left\{ \cos (\alpha) \sin ^{-1}(\cot (\alpha) \cot (\beta)) -\tan ^{-1}\left(\frac{\cos (\beta)}{\sqrt{\sin ^2(\beta)-\cos ^2(\alpha)}}\right)\right\}+\pi r^2 (1-\cos (\alpha)). $$

Note that the solution is defined as a function of $\alpha$ and $\beta$. If we change the value of $\alpha $ and $\beta$, the area of P into A will change eventually.

Now consider more complex case where $P$ and $S$ are not equal hemisphere. enter image description here

Question: If $P$ and $S$ are not equal hemisphere rather they are spherical cap, then what I need to consider to calculate the area of $P$ into zone $A$ as a function of $\alpha$ and $\beta$? Here $\gamma$ defines size of the spherical cap and r1 is the radius of the base of the cap. Do I need to introduce any other parameter?

T. an
  • 159

1 Answers1

0

It is confusing that you use $\theta$ for both the azimuthal coordinate, and the offset of the spherical cap. Let us change the notation, so the offset is described by an angle $\gamma$ in your second figure. You should also label your axis, let's say the vertical axis is $z$, and the horizontal one is $x$, while $y$ is perpendicular to the page. With these definitions, the equation for the boundary of the spherical cap is $$ z = x\tan \beta - r\sin \gamma $$ while the points on the sphere are described by $$ z = r\cos \theta $$ $$ x = r\sin \theta \sin \phi $$ $$ y = r\sin \theta \cos \phi $$

Plugging one in the other, we find the relationship between $\theta$ and $\phi$: $$ \cos \theta = \sin \theta \sin \phi \tan \beta - \sin \gamma $$

The smallest $\theta$, or the tip of the cap, is found when $\phi = \pi/2$: $$ \cos \theta_0 = \sin \theta_0 \tan \beta - \sin \gamma $$ from which we find $$ \theta_0 = -\beta + \cos^{-1} (-\cos \beta \sin \gamma) $$

So the area is $$ A/r^2 = \int_{-\beta + \cos^{-1} (-\cos \beta \sin \gamma)}^{\alpha} d\theta\; \sin \theta \left(\pi - 2\sin^{-1} \left[\frac{\cos \theta+\sin \gamma}{\sin \theta \tan \beta} \right] \right)$$

Airidas Korolkovas
  • 123