Calulate area when two circle intersect each other

Question

I have Sphere with radius R. Inside the sphere I have Two circle. One circle is fixed defined by $\alpha$. Another circle can rotate and the orientation of that circle can be defined by $\beta$. From the centre of the sphere until the edge of the movable circle create $\alpha$ angle with $z$ axis. $h$ and $a$ are distance from the origin and base radius of this circle .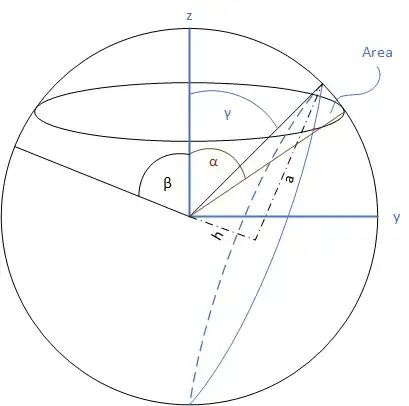

Now when both circle intersect each other what will be the surface area of intersection? Using spherical coordinate system $r,\theta,\phi$, I know that my $\theta $ limit goes from $\gamma$ to $\alpha$. But I am not getting the limit for $\phi$ with this given parameters. I am trying to calculate the intersected surface area using only calculus and trigonometry for relevancy of my future problem.

Answer 1

I'll change the problem statement a little so I can use Cartesian coordinates at first.

Also let $R=1$, since we can always multiply the answer by $R^2$.

Let Circle 1 lie in the horizontal plane with elevation $d$ (Plane 1).

Let Circle 2 lie in the plane defined by the radius vector $\vec{h}$ (Plane 2).

Equation of Plane 1:

$$z=d$$

Equation of Plane 2:

$$h_x x+h_y y+h_z z=h^2$$

Equation of the sphere:

$$x^2+y^2+z^2=1$$

Now we transition to spherical coordinates:

$$x = r \sin \theta \cos \phi$$

$$y = r \sin \theta \sin \phi$$

$$z = r \cos \theta$$

Which gives us:

$$r=1$$

$$\cos \theta=d$$

$$h_x \sin \theta \cos \phi+h_y \sin \theta \sin \phi+h_z \cos \theta=h^2$$

We now have equations to determine the intersection points of the two circles on the sphere.

$$\pm \sqrt{1-d^2}(h_x \cos \phi+h_y \sin \phi)+h_z d=h^2$$

$$h_x \cos \phi+h_y \sin \phi= \pm\frac{h^2-h_z d}{\sqrt{1-d^2}}$$

Define:

$$h_x=\cos \delta, \qquad h_y= \sin \delta$$

Then we have:

$$\cos (\phi-\delta)=\pm\frac{h^2-h_z d}{\sqrt{1-d^2}}$$

$$\phi= \delta+\arccos \left(\pm \frac{h^2-h_z d}{\sqrt{1-d^2}} \right)$$

$$\phi= \arccos h_x+\arccos\left(\pm \frac{h^2-h_z d}{\sqrt{1-d^2}} \right)$$

$$\theta=\arccos d$$

We found the intersection point coordinates (note also the condition for their existence):

$$-1 \leq \frac{h^2-h_z d}{\sqrt{1-d^2}} \leq 1$$

I think now half of the problem is solved, since we can use those points to set up the limits of integration on the surface of the sphere.