If $\sin(18^\circ)=\frac{a + \sqrt{b}}{c}$, then what is $a+b+c$?

Question

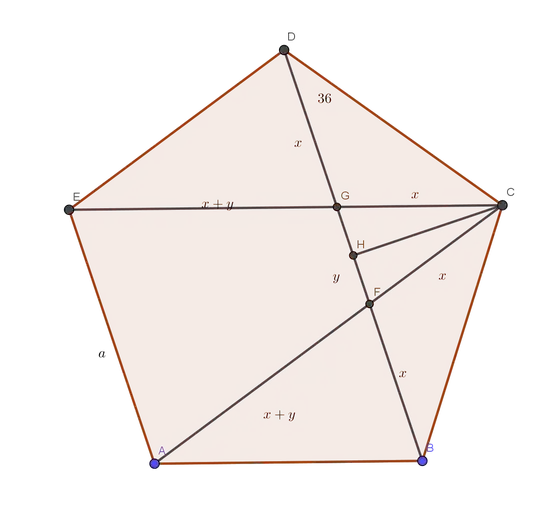
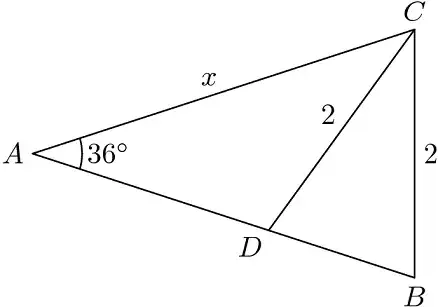
If $\sin(18)=\frac{a + \sqrt{b}}{c}$ in the simplest form, then what is $a+b+c$? $$ $$ Attempt: $\sin(18)$ in a right triangle with sides $x$ (in front of corner with angle $18$ degrees), $y$, and hypotenuse $z$, is actually just $\frac{x}{z}$, then $x = a + \sqrt{b}, z = c$. We can find $y$ as $$ y = \sqrt{c^{2}- (a + \sqrt{b})^{2}} $$ so we have $$ \cos(18) = \frac{y}{z} = \frac{\sqrt{c^{2}- (a + \sqrt{b})^{2}}}{c}$$

I also found out that $$b = (c \sin(18) - a)^{2} = c^{2} \sin^{2}(18) - 2ac \sin(18) + a^{2}$$

I got no clue after this.

The solution says that $$ \sin(18) = \frac{-1 + \sqrt{5}}{4} $$

I gotta intuition that we must find $A,B,C$ such that $$ A \sin(18)^{2} + B \sin(18) + C = 0 $$ then $\sin(18)$ is a root iof $Ax^{2} + Bx + C$, and $a = -B, b = B^{2} - 4AC, c = 2A$.

Totally different. This question is not asking to prove that $sin(18)=(-1+\sqrt{5})/4$, that is just part of the solution.

Probably you're supposed to use the fact that $18^\circ$ is the same as ${\pi\over10}$ radians. I'd start looking at $\sin(5\theta)$ — saulspatz, May 18 '19 at 15:49
Use https://math.stackexchange.com/questions/827540/proving-trigonometric-equation-cos36-circ-cos72-circ-1-2 — lab bhattacharjee, May 18 '19 at 15:56
You probably want to stop $\frac{a+\sqrt{b}}{c}=\frac{na+\sqrt{n^2b}}{nc}$ from changing your $a+b+c$. — user10354138, May 18 '19 at 16:13
@MariaMazur totally different question.. proving $sin(18)=...$ does contribute largely to the solution, but that is not the question. — Redsbefall, May 19 '19 at 18:23
This question was already closed, I reopen it by mistake and then reclose it. — nonuser, May 19 '19 at 18:24
@MariaMazur but it is not a duplicate. This is a contest math problem. — Redsbefall, May 19 '19 at 18:29
And what do you want now? To reopen it? Why? You already accept an aswer. — nonuser, May 19 '19 at 18:30

score 8 · Answer 1 · edited May 18 '19 at 16:42

8

Let $A = 18°$
$$5A = 90°$$ $$⇒ 2A + 3A = 90˚$$ Taking sine on both sides, we get $$\sin 2A = \sin (90˚ - 3A) = \cos 3A $$ $$⇒ 2 \sin A \cos A = 4 \cos^3 A - 3 \cos A$$ $$⇒ 2 \sin A \cos A - 4 \cos^3A + 3 \cos A = 0 $$ $$⇒ \cos A (2 \sin A - 4 \cos^2 A + 3) = 0 $$ Dividing both sides by cos A $$⇒ 2 \sin A - 4 (1 - sin^2 A) + 3 = 0$$ $$⇒ 4 \sin^2 A + 2 \sin A - 1 = 0$$ After solving this quadratic $$ \sin18°=\frac{-1+√5}{4}$$

edited May 18 '19 at 16:42

John Doe

14,545

answered May 18 '19 at 15:55

Abhishek Kumar

1,121
9
28

How you got $\cos 3A$? – nonuser May 18 '19 at 16:30
$sin (90° - \theta) =cos\theta$ – Abhishek Kumar May 18 '19 at 16:33
Not that........ – nonuser May 18 '19 at 16:34
So what explain more what you what to ask – Abhishek Kumar May 18 '19 at 16:35
In next line there is no $\cos 3A$. Where it go? – nonuser May 18 '19 at 16:36
$cos3\theta=4cos^3\theta-3cos\theta$ – Abhishek Kumar May 18 '19 at 16:41
And how you got that? – nonuser May 18 '19 at 16:41
@MariaMazur $$\begin{align}\cos(3\theta)=\Re(e^{3i\theta})&=\Re((\cos\theta+i\sin\theta)^3)\&=\cdots\&=\Re(4\cos^3\theta-3\cos\theta+3i\sin\theta-4i\sin^3\theta)\&=4\cos^3\theta-3\cos\theta\end{align}$$ – John Doe May 18 '19 at 16:45
Go through https://math.stackexchange.com/questions/852122/picture-intuitive-proof-of-cos3-theta-4-cos3-theta-3-cos-theta/852230 – Abhishek Kumar May 18 '19 at 16:46
@MariaMazur the relation can be obtained using simple sine and cosine rules: $$\cos(3x) = \cos(x + 2x) = \cos(x) \cos(2x) - \sin(x) \sin(2x) $$ $$ = \cos(x) (\cos^{2}(x)-\sin^{2}(x)) - 2 \sin^{2}(x) \cos(x) $$ $$ = \cos(x)(2 \cos^{2}(x)-1) - 2 (1 - \cos^{2}(x)) \cos(x) $$ $$ = 4 \cos^{3}(x) - 3 \cos(x)$$ – Redsbefall May 19 '19 at 07:44
I know how to get $\cos 3x$. It is a missing detail which should be included in the answer. @AriefAnbiya – nonuser May 19 '19 at 08:07

David C. Ullrich · Answer 2 · 2019-05-19T15:09:52.997

6

Edit: This is now obsolete - it applies to the original version of the question, without the condition "in simplest form":

It's clear that $a+b+c$ is not determined, since $$\frac{2a+\sqrt{4b}}{2c}=\frac{a+\sqrt b}c$$but $$2a+4b+2c\ne a+b+c.$$

edited May 19 '19 at 15:09

answered May 18 '19 at 16:56

David C. Ullrich

89,985

I like that all other answers went for lot of calculation, not one answering the original question while in fact it can be decided by simple considerations that the problem is missing constraints. – zwim May 18 '19 at 17:02
Explain me more please – Abhishek Kumar May 18 '19 at 17:11
@AbhishekKumar The point is that, from a technical point of view, the question cannot be answered. Consider that you could write $\frac{−1+\sqrt5}4$ as $\frac{−2+\sqrt{20}}8$ or $\frac{−100+\sqrt{50000}}{400}$, etc., each of which corresponds to a different result for $a+b+c$. The question would need to specify something like "... where $a,b,c \in \Bbb Z$ and $b$ is square free." – Théophile May 19 '19 at 06:04
Yes you are correct, they must give some constraints to get the specific value of $a, b, c$ – Abhishek Kumar May 19 '19 at 06:27
But $\frac{2a+ \sqrt{4b}}{2c}$ is not in simplest form... – Redsbefall May 19 '19 at 07:31
1

@AriefAnbiya The point to my post was precisely that there must be a condition missing. Indeed, "in simplest form" was added fifteen hours after I posted this. – David C. Ullrich May 19 '19 at 15:07

score 5 · Answer 3 · edited May 20 '19 at 18:04

Let $ABCDE$ be a regular pentagon.

In right triangle $GHC$ we see $\sin 18^{\circ} = {y\over 2x} $. Let $k=y/x$.

From triangle similarity of $GFC$ and $ACE$ we have $${x\over y} = {2x+y\over a}$$

and from triangle similarity of $BFC$ and $EDC$ we have $${a\over x} = {2x+y\over a}$$

Eliminate $a = {x^2\over y}$ and we get $$x^3 = y^2(2x+y)\implies k^3+2k^2-1 =(k-1)(k^2+k-1)=0 $$

Clearly $k\ne -1$ so $$k_{2,3} = {-1\pm \sqrt{5}\over 2} $$ and so $$\sin 18^{\circ} = {-1+ \sqrt{5}\over 4} $$

CY Aries · Accepted Answer · 2019-05-18T16:14:51.497

2

In the figure, let $AB=AC=x$. Note that $AD=CD=2$. As $\triangle ABC\sim\triangle CDB$, $\dfrac x2=\dfrac 2{x-2}$

So, $x^2-2x-4=0$ and hence $x=1+\sqrt{5}$.

$\sin18^\circ=\dfrac 1x=\dfrac{\sqrt{5}-1}4$.

edited May 18 '19 at 16:14

answered May 18 '19 at 16:03

CY Aries

23,393

A beautifully simple answer! – Théophile May 19 '19 at 06:07

Travis Willse · Answer 5 · 2019-05-19T15:09:57.023

Hint This is a classic problem and probably a duplicate here, but I was unable to find another instance of this question as written. Edit Found one.

First, note that $\sin 18^\circ = \cos 72^\circ$; we find the latter.

Recall that (for $n \geq 2$) the sum of the $n$th roots of unity sum to zero, and taking real parts leaves $$\sum_{k = 0}^{n - 1} \cos \left(\frac{k}{n} \cdot 360^\circ\right) = 0 .$$ Setting $n = 5$ and using the symmetry of the cosine function gives $$1 + 2 \cos 72^\circ + 2 \cos 144^\circ = 0 .$$ Using the double angle formula---in particular that $$\cos 144^\circ = 2 \cos^2 72^\circ - 1$$ ---and substituting in the previous display equation gives a quadratic expression in $\cos 72^\circ$: $$4 \cos^2 72^\circ + 2 \cos 72^\circ - 1 = 0 .$$ By the quadratic equation, $$\cos 72^\circ = \frac{-2 + \sqrt{(2)^2 - 4 (4) (-1)}}{2(4)} = \frac{-1 + \sqrt{5}}{4} .$$ (To resolve the $\pm$ ambiguity it's enough to know that $\cos 72^{\circ} > 0$.)

Thanks, I've fixed this. – Travis Willse May 19 '19 at 16:46 — Travis Willse, May 19 '19 at 16:46

If $\sin(18^\circ)=\frac{a + \sqrt{b}}{c}$, then what is $a+b+c$?

5 Answers5