1

Could you please explain, how one gets this Parametric representation of a solid trapezoid ? I mean the procedure and not the answer. I have some linear geometry (as polygons), and I need to represent them in the parametric form. I have no idea how to get the parametric form of the rectangle or triangle and how to build the complex geometries (like trapezoid). May be some hints or where can I find it in the literature? Here are the examples of my geometries.

Example Geometry 1 Example Geometry 2

Community
  • 1
Ekaterina Deriabina
  • 11
  • Welcome to stackexchange. In order for us to help you we need much more context. Please [edit] the question to show us a few particular polygons you care about, and why, so we can see how you are representing them. You seem to want a map from the unit square to your polygon. There is probably no easy way to do that in general.. Are you looking for an algorithm? – Ethan Bolker May 08 '19 at 15:09
  • 1
    Possibly helpful: https://math.stackexchange.com/questions/315828/transformation-between-square-and-a-polygon – Ethan Bolker May 08 '19 at 15:14
  • I have taken the liberty to modify your title in order to attract more attention for future readers. Furthermore, I have added tag "polygons". – Jean Marie May 09 '19 at 06:34
  • It is unclear if you want to parameterize the outlines or the whole area. Maybe better to tell us why you need that. Sounds like an XY question. –  May 10 '19 at 09:54
  • I need to parametrize the outlines, as I need to find the coordinates of the surface points. So the coordinates of the outlines in a parametric form – Ekaterina Deriabina May 10 '19 at 09:57

1 Answers1

7

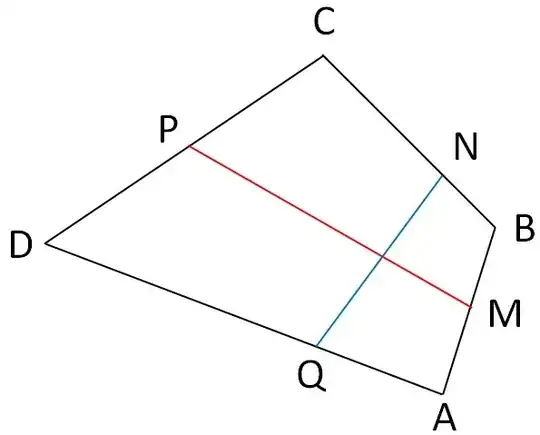
Here are two different parametrization methods for a convex quadrilateral $ABCD$, a trapezoid being a particular case.

First method : ("bilinear interpolation", using barycentric principles)

a) on the two opposite sides $AB$ and $DC$, using a first parameter $0 \leq u \leq 1$, define $M:=(1-u)A+uB \in [AB]$ and $P:=(1-u)D+uC \in [DC].$

b) on the two other opposite sides $BC$ and $AD$, using a second parameter $0 \leq v \leq 1$, define $N:=(1-v)B+vC \in [BC]$ and $Q:=(1-v)A+vD \in [AD].$

The point at the intersection of line segments $[MP]$ and $[NQ]$ is defined in a unique way by coordinate pair $(u,v)$ ; in a reciprocal manner, every point interior to the quadrilateral has such a representation.

enter image description here

Fig. 1 : the case $u=1/2$ ($M$ and $P$ are the midpoints of their line segments), and $v=1/3$.

This mapping method is called bilinear interpolation.

Grouping operations a) and b) above, one obtains the coordinates of the intersection point as

$$\begin{cases}x& = &\color{red}{(1-v)}(\color{blue}{(1-u)}x_A+\color{blue}{u}x_B)+ \color{red}{v}(\color{blue}{(1-u)}x_D+\color{blue}{u}x_C) \\ y& = &\color{red}{(1-v)}(\color{blue}{(1-u)}y_A+\color{blue}{u}y_B)+ \color{red}{v}(\color{blue}{(1-u)}y_D+\color{blue}{u}y_C)\end{cases}$$

or, in a simplified form :

$$\begin{cases}x& = &a+bu+cv+duv \\ y &= &e+fu+gv+huv\end{cases}\tag{1}$$

for certain fixed coefficients $a,b,...h$.

References :

Remark : this transformation is not amenable to a projective transform (see below) because for exemple lines $AB$, $CD$ and $NQ$ do not intersect into a single point.

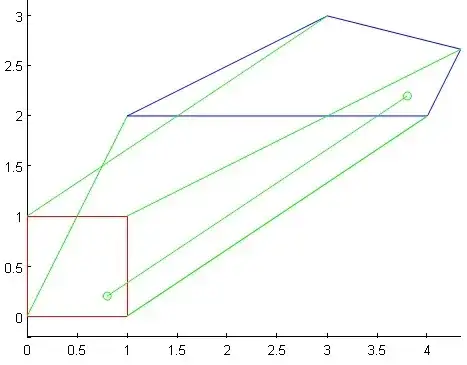
2nd method : (projective transformation)

Convex quadrilateral $ABCD$ could as well be considered as the image by a projective transformation of a reference square $[0,1] \times [0,1]$ with natural coordinates $(u,v)$ that will be "mapped" onto the quadrilateral. In this case, we have to find the matrix entries of the corresponding homography.

If for example, we want to "map" the reference square with current point $(u,v) \in [0,1] \times [0,1]$, to the quadrilateral given on the figure below, we will use the projective transformation :

$$x=\dfrac{au+bv+c}{gu+hv+1}, \ \ \ y=\dfrac{du+ev+f}{gu+hv+1}\tag{2}$$

with fixed coeffients that we store in a so-called homography matrix :

$$H=\begin{pmatrix}a&b&c\\d&e&f\\g&h&1\end{pmatrix}=\begin{pmatrix}7&5&1\\2&4&2\\1&1&1\end{pmatrix}$$

(please note the common denominator). Check for example that the image of vertex $(0,0)$ on the square is vertex $(1,2)$ on the quadrilateral.

The entries of matrix $H$ are obtained through 8 equations expressing that the image of $(0,0)$ is $(x_A,y_A)$ (known quantities), the image of $(0,1)$ is $(x_B,y_B)$, etc.

Being able to go the other way (knowing (x,y), find $(u,v)$, is essential. We need for that inverse formulas that are readily obtained : they belong to the same family of projective transformations with coefficients the entries of $H^{-1}$...

enter image description here

Fig. 2 : Points $(u,v)$ are related to their images $(x,y)$ by a green line segment.

Appendix : Matlab program that has generated Fig. 2 :

i=complex(0,1);
R=[7,5,1,2,4,2];
a=R(1);b=R(2);c=R(3);d=R(4);e=R(5);f=R(6);
Z=@(x,y)((a*x+b*y+c)./(x+y+1)+i*(d*x+e*y+f)./(x+y+1));
plot(Z([1,1,0,0,1],[0,1,1,0,0]),'b');axis equal
plot([1,1,0,0,1],[0,1,1,0,0],'r')
plot([1+0i,Z(1,0)],'g')
Jean Marie
  • 81,803