Manhattan distance problem with infinite zig zags

Question

If you turn left/right any finite number of times going from point to point, it will be the same as if you traveled $x$ then turned once and traveled $y$ to get there. I hear that even an infinite number of turns will not suddenly shorten the distance to $\sqrt{x^2+y^2}$.

We have a similar situation in the staircase problem in which $\pi \ne 4$ because something happens [forgive me] at infinity. We no longer have size to the xy vectors. We have a set of points that coincide with the curve that is a circle.

Here, we have a set of points that are $not$ $close$ $to$, but $on$ the line that is the hypotenuse of a right triangle.

In the staircase problem, we still have an infinite number of vectors not pointing in the direction of the curve except at four points. How does the Manhattan distance differ from $\pi \ne4$ in the staircase problem above where we know the answer $\pi$ as a given?

I never learn why the staircase problem ends up as $3.14...$. Could we need new theorems to explain both of these? Or will they both forever be nothing more than paradoxes? Perhaps the staircase problem has no answer. Can someone verify that that it always results in $\pi=4$? If so, I can accept that the Manhattan distance never changes.

Answer 1

The final endpoint is reached by summing a set of vectors. Each of those vectors is aligned with either the $x$-axis or the $y$-axis. Now use the fact that vector addition is commutative to reorder the vector sum into one part that contains only the $x$-aligned vectors, and the other part only the $y$-aligned vectors. Then sum each of those parts separately. The answer should be obvious. And nothing changes if you construct some kind of Manhattan fractal path with an infinite number of vectors.

The Koch snowflake is different because in that case, for each iteration of the fractal construction, the perimeter increases, and it doesn't converge to any finite value in the limit.

Answer 2

If you turn left/right any finite number of times going from point to point, it will be the same as if you traveled $x$ then turned once and traveled $y$ to get there. I hear that even an infinite number of turns will not suddenly shorten the distance to $\sqrt{x^2+y^2}$.

We have a similar situation in the staircase problem in which $\pi \ne 4$ because something happens [forgive me] at infinity. We no longer have size to the xy vectors. We have a set of points that coincide with the curve that is a circle....

It appears that the distance snaps to a new value at the magical point of infinity.

Looking for an answer drawing from credible and/or official sources.

I would like an answer that considers both the Staircase Problem and the Manhattan problem and shows me how they correspond or differ.

I think the considered paradoxes are of ancient Greek style and the key point here is to understand what is a distance and the length of a path.

The length of a curve is not its “abstract” property, but has a concrete definition via agreeing measurements. One of corollaries of this definition is the staircase paradox, which shows that curves which are arbitrary close as sets (with respect to Hausdorff distance) can have different lengths. But this is OK, because a curve is not only a set, but a set with a given walk along it. We see that the lenght of the limit of constant length curves can collapse, because in the limit case we lose a dimension for wiggling which increases a way and we are forced to go “straight” (that is, towards the tangent direction, infinitesimally).

Manhattan distance $d((0,0),(x,y))$ from $(0,0)$ to $(x,y)$ is defined to be $|x|+|y|$. If $P$ is any monotone path from $(0,0)$ to $(x,y)$ consisting of countably many axis-aligned segments (by the way, a monotone path has countably many (that is at most $\aleph_0$) such segments, because their projections on the respective axis has mutually disjoint interiors) then, according to a definition of the length of a curve in a metric space (see here), the length of $P$ with respect to the standard Euclidean distance on the plane equals the length of $P$ with respect to Manhattan distance. But this fails for a general case. Whereas the length of any monotone path with respect to Manhattan distance is the Manhattan distance between its endpoints (in this sense “the Manhattan distance never changes”), the Euclidean length of a hypotenuse of a triangle with axis-aligned legs of lengths $x$ and $y$ is $\sqrt{x^2+y^2}$.

Answer 3

Perimeter, surprisingly, isn't continuous.

What this means is that you can find shapes that are very similar to each other but which have different perimeters. You can also find a sequence of shapes that get more and more similar to a target shape, but don't get closer and closer in perimeter.

The reason is because you can take any shape and add an imperceptibly small amount of wiggle all around to the perimeter in order to change its perimeter without affecting its shape very much. The new object may make contact with the old object in many places, but because of the wiggles, their perimeters will not match. The way perimeter works, you do not need a large amount of wiggle in order to affect perimeter, just a large number of very small wiggles.

For example, consider the following sequence of line drawings. Each iteration, the number of "bumps" doubles, but their height is scaled by some amount (shown by the orange dotted line). In successive rounds, the shapes get closer and closer to the flat line shown at the bottom.

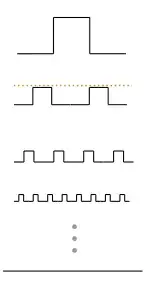
Their perimeter, however, is another story. Note that if you add up the horizontal line segments at any stage of this process, you get the full length of the flat line at the bottom. So there's a little extra length at each stage, which is contributed by the vertical components. That extra amount means a lot: depending on how the height is scaled, the objects' perimeter could approach any number at all.

• If the height is scaled in half each time, then the overall vertical components don't change, so the objects' perimeter stays the same at each stage— the number of bumps doubles, but their height is halved each time. This is exactly like the Manhattan distance example.
• If the height is scaled by a number larger than one half, then the perimeter will actually grow each iteration, because the doubling of the bumps outpaces the shrinking height.
• If the height is scaled by a number less than one half, then the perimeter will shrink each iteration. The vertical components will eventually vanish, so that in the limit ("at infinity") the two shapes will match in shape and in perimeter.

It's basically a strange fact about length that you can take a shape and add a lot of imperceptibly tiny wiggles along its perimeter to make an object that looks basically identical but has a radically, fractally different perimeter. In higher mathematics, this intuitive idea is formalized in various ways; for example, the way in which, in inverse problems, small amounts of noise can lead to arbitrarily large differences in the inferred model.

---

As for the staircase and Manhattan problems, both are examples of shapes that get closer and closer to some target shape whose length is known. In the case of the circle, the target length is known to be the circumference $\pi$. In the case of Manhattan distance, the target length is known to be the length of the hypotenuse, $\sqrt{x^2+y^2}$. Both examples use the perimeter trick to make a sequence of objects that get more and more similar to the target shape, but where the perimeters do something else entirely.

It doesn't matter how many times the curve touches the target shape because—essentially— wherever you're not touching the shape, you can wiggle and add however much extra perimeter you like. In fact, touching in more and more places gives an opportunity to add more and more (imperceptibly tiny, but crucial) deviations in between the places of contact.

Answer 4

From the OP: "We have a set of points that coincide with the curve that is a circle."

This is not the case. Note that at each iteration, only a finite number of points of the staircase shape touch the circle. Furthermore, in the linked image, if we take the circle to be centered at the origin with radius 0.5, and the staircase iteration function to be subdividing each interval in half, then the points of the staircase that do touch the circle all have x-coordinates of the form $\frac{i}{2^j}$ for some integers $i$ and $j$. In particular, points with irrational x-coordinates -- e.g.: $(\frac{\sqrt{6}}{4}, \frac{\sqrt{2}}{4})$ -- are never touched by the staircase, only approached arbitrarily closely.

The same reasoning applies to the staircase shape approaching the hypotenuse of a right triangle. There will always be points on the hypotenuse that are not touched by the staircase, so the OP's declaration that "Here, we have a set of points that are not close to, but on the line that is the hypotenuse of a right triangle." is also false.