4

Motivating problem: https://artofproblemsolving.com/wiki/index.php/2010_AMC_10A_Problems/Problem_22

If we draw a triangle in the interior of a circle, it is straightforward to show that the triangle can be constructed by the intersection of chords drawn between 6 points on the circle. This can be done by extending each side of the triangle until it intersects with the circle.

I am unable to prove that if we start with six points on the circle, and draw chords between all points, that only one triangle is formed in the circle's interior. I've listed some related questions below but I don't think these questions are quite what I'm looking for.

Related questions:

3 Answers3

2

To get an interior triangle, you need three chords that form the sides of the triangle. Any two of those chords intersect to form a vertex of the interior triangle. Obviously two intersecting chords cannot share an endpoint, so the six points on the circle must each be the endpoint of one of the three chords forming the triangle.

If the 6 points on the circle are labelled A to F in order, then you must connect A to D, B to E, C to F to get the chords that form the sides of the triangle. Any other choice won't work because every chord must intersect the two others (to get the two vertices on that side of the triangle) and therefore has two endpoints on either side. This pairing AD, BE, CF is unique, so there is a unique interior triangle.

Jaap Scherphuis
  • 13,660
0

Indeed, there is only one interior triangle. Here is the full mesh:

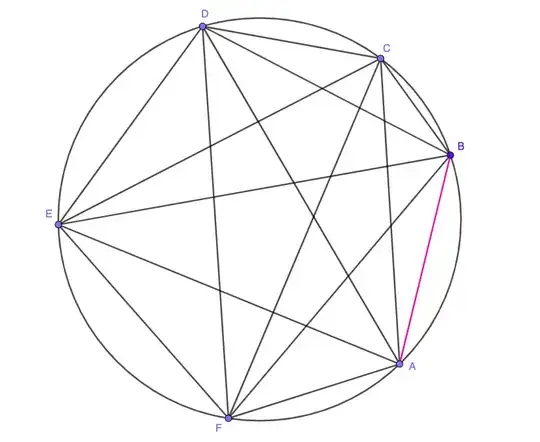
enter image description here

Look at the point $A$. Can we create an interior triangle if we connect $A$ with it's nearest neighbor (WLOG, we can assume that it's point B, see picture). The answer is - no! Because there is no other chord intersecting chord $AB$ you cannot create an interior point of your triangle. So you can eliminate segments $AB$, $BC$, $CD$, $DE$, $EF$, $FA$.

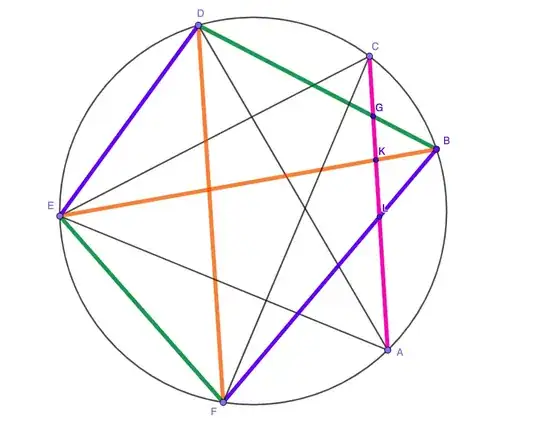
enter image description here

If we cannot create an interior triangle with chord $AB$, maybe we can do that if we connect $A$ with $C$ or $E$. These two cases are equivalent - basically, you take point $A$, skip the first neighbor clockwise or counterclockwise and select the next neighbor. WLOG we can assume that it's point $C$. Notice that point $B$ and points $D,E,F$ are on different sides of chord $AC$. So it's guaranted that chord $AC$ and chords $BD$, $BE$, $BF$ intersect at points $G,K,L$. These three points are candidates for trinagle interior points.

However, If you pick $AC$ and $BD$, the remaining points $E,F$ are neighbors and the third chord $EF$ does not intersect with any of them. If you pick $AC$ and $BF$, points $D,E$ are neighbors and the third chord $DE$ does not intersect either. In the last case you have chords $AC$ and $BE$. The third chord is $DF$. But points $D,F$ are on the same side of chord $AC$ and therefore chords $AC$ and $DF$ do not intersect and do not form the interior point of the triangle.

enter image description here

The last option is to connect $A$ with the opposite point $D$. Do the same for points $B$ and $E$. Chords $AD$ and $BE$ do intersect because points $B,E$ are on different sides if chord $AD$. That creates one interior point of the triangle. In the same way you can show that it's guaranteed that $BE$ and $CF$ intersect (second interior point of the triangle). The third interior point is created by intersecting chords $AD$ and $CF$.

In this last case you should also show that you cannot create an interior triangle by selecting chord $AD$ and any other chord with end point $B$ excpet $BE$. This is obvious: $BA,BC,BD$ are ruled out because these chords do not create interior points with chord $AD$. If you choose $BF$, the third chord would be $CE$ and that chord does not intersect with $BF$ and you don't get an interior point.

So you have only one interior triangle formed. That triangle is always formed by chords $AD,BE,CF$. If these three segments concur, the interior triangle disappears.

Saša
  • 15,906
  • Thank you for the extremely thorough answer. The diagrams were particularly useful in simplfying the problem. What tool did you use to generate the diagrams? –  May 03 '19 at 13:48
  • @recreationalmath You're welcome! I have used Geogebra: https://www.geogebra.org/classic – Saša May 03 '19 at 14:45
0

I guess more correct expression is

"Drawing all chords between six points on a circle, prove that at most one triangle can be formed in the circle's interior."

Now for six points on the circle we have 15 chords. Among these chords there are chords formed by adjacent points on circle, so they do not have intersection points, so we rule out these chords, there are 6 chords like this.

Now there are another set of chords which are formed by two points which have only one point between them on one side of the circle, like AC, which has only B on one side (considering points A,B,C,D,E,F on the circle). Now we have three distinct intersection points on this chord (as other side there are three distinct points (D,E,F).

Now considering the possibility that any two points out of this three can form side of the triangle. We see that for any of the two points the chords are diverging from the common point (i.e. B), as the supposed triangle should be on the other side of the B and the chords are diverging towards the other side we can not form triangle by any of these two points. Again there are 6 chords like this, so we rule out this 6 chords also.

Finally we are left with only three chords. Now with three line segments in any case we can always form only one triangle (at most). When all these three intersection points fall on each other, we will not have any triangle.

amitava
  • 838