If there are N points on a circle, and you draw a chord between each of them, how many regions is the circle subdivided into?
I'm not quite sure where to begin. I know that there are at least n section for n points on a chord because if you connect each point on the circle with its adjacent point then that forms n sections. Whatever goes on in the middle though seems really arbitrary. Is there any good way of approaching this problem?
Thanks
Let's assume that no three lines intersect at the same point.
Consider what happens each time you add a line between two points. If it crosses $k$ other lines, it splits $k+1$ regions into two, thereby adding $k+1$ regions. Therefore, when a line is added, it can be considered to be adding $1$ region for the line and $1$ region for each point of intersection:
$\hspace{4.5cm}$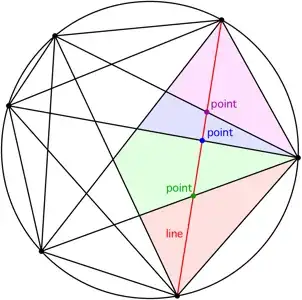
$$
\text{Regions Split by a Line}\atop\text{Each Region is Paired with a Line or Point of Intersection}
$$
Thus, we just need to count $1$ for the original region inside the circle, and add the number of lines, $\binom{N}{2}$, and the number of intersections, $\binom{N}{4}$.
Thus, there are $\binom{N}{4}+\binom{N}{2}+\binom{N}{0}$ regions.
Counting Lines and their Intersections
Note that given $N$ points on the circle, each pair of points yields a line, thus the number of lines connecting the points is $\binom{N}{2}$. For each set of $4$ points, there is a unique intersection of two lines, an "X in a quadrilateral" arrangement. Thus, the number of interior line intersections is $\binom{N}{4}$.
Non-Sequitur:
This is often given as an example of what happens if you attempt to guess a sequence from the first few terms since this sequence starts with $$ 1,2,4,8,16,\dots $$ but the next term is $31$.
Why:
The reason for the initial similarity of $\binom{n}{4\vphantom{0}}{+}\binom{n}{2\vphantom{0}}{+}\binom{n}{0}$ to the geometric progression is that $$ \sum_{k=0}^\infty\binom{n}{k}=(1+1)^n=2^n\tag{1} $$ and $$ \sum_{k=0}^\infty(-1)^k\binom{n}{k}=(1-1)^n=0^n\tag{2} $$ For $n>0$, adding $(1)$ and $(2)$ and dividing by $2$ gives $$ \sum_{k=0}^\infty\binom{n}{2k}=2^{n-1}\tag{3} $$ $\binom{n}{4\vphantom{0}}{+}\binom{n}{2\vphantom{0}}{+}\binom{n}{0}$ is the first three terms of $(3)$. The first time a non-zero term is left out of $(3)$ is when $n=6$, and that is when $\binom{n}{4\vphantom{0}}{+}\binom{n}{2\vphantom{0}}{+}\binom{n}{0}=31$.
