4

We have $n$ point on the circumference of a circle. We draw all chords between these points. No three chords are concurrent.

How many triangles exist that their apexes could be on circumference of the circle or intersection points of chords and side of triangles is on chords?

Things I have done so far:

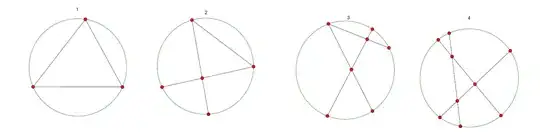
There are four situations: enter image description here

  • situation #$1$:all points on circumference.
  • situation #$2$:two points on the circumference, one intersection point.
  • situation #$3$:one point on the circumference, two intersection points.
  • situation #$4$:three intersection points.

Situation #1 is easily countable. ${n \choose 3}$

For other situations, I can't find a way for counting them.

Answer (according to answer key): $${n \choose 3} + 4{n \choose 4} + 5{n \choose 5} + {n \choose 6}$$

Sayem Rahman
  • 184
user2838619
  • 3,120

1 Answers1

3

Situation $2$:

For each selection of any $4$ points on the circumference, you can draw the diagram you have. The line segment that joins the adjacent circumference points, could instead join any of the $4$ pairs of adjacent circumference points, so we have $4$ different triangles for each choice of $4$ circumference points.

There are $\binom{n}{4}$ ways to choose the $4$ points, so Situation $2$ contributes:

$\qquad4 \binom{n}{4}$ triangles.

Situation $3$:

For each selection of any $5$ points on the circumference, you can draw the diagram you have. You could choose any of these $5$ points to be a vertex of a Situation $3$ triangle, so we have $5$ different triangles for each choice of $5$ circumference points.

There are $\binom{n}{5}$ ways to choose the $5$ points, so Situation $3$ contributes:

$\qquad5 \binom{n}{5}$ triangles.

Situation $4$:

For each selection of any $6$ points on the circumference, you can draw the diagram you have. There is only one way to construct that internal triangle given these $6$ circumference points.

There are $\binom{n}{6}$ ways to choose the $6$ points, so Situation $4$ contributes:

$\qquad \binom{n}{6}$ triangles.

Mick A
  • 10,208