Visualizing the Lie Bracket in connection with Torsion

Question

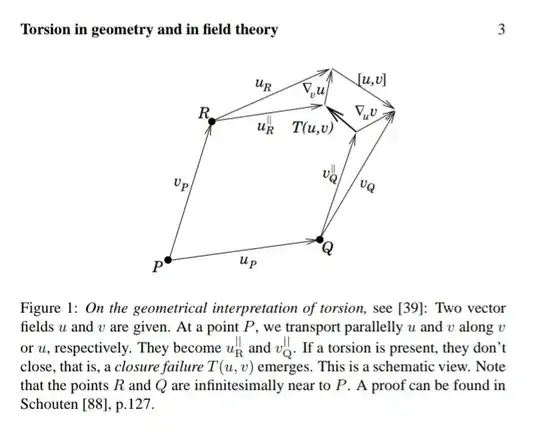
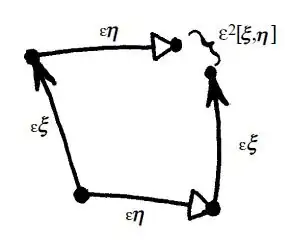
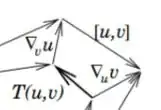
I have seen this kind of picture a lot, linking the Lie Bracket with the Torsion (e.g. 1, 2, 3, 4).

I will report for convenience one of such picture, from Hehl and Obukhov review article

For some reason I am not able to understand how the Lie Bracket can be seen in that way. I will say what I have done so far, I would be glad if someone would point me to the missing piece or maybe if I am misunderstanding the approximation done.

Let us take two vector fields $u$ and $v$ on a manifold $M$. Choose a $P\in M$, we can say that $$ u_P = u^k \left( \frac{\partial}{\partial x^k} \right)_P $$ $$ v_P = v^k \left( \frac{\partial}{\partial x^k} \right)_P $$

Let me say with abuse of notation that $R=P+\epsilon v$ and $Q=P+\epsilon u$ (I believe the formal way would be to go down in the chart and then coming back with the inverse). Anyway $u$ in $R$ is $$ u_R \approx \left( u^k +\epsilon v^i \frac{\partial u^k}{\partial x^i} \right) \left( \frac{\partial}{\partial x^k} \right)_R \approx \left( u^k + \epsilon v^i \frac{\partial u^k}{\partial x^i} + \epsilon v^i u^j \Gamma_{ij}^k + O(\epsilon^2)\right) \left( \frac{\partial}{\partial x^k} \right)_P $$ while the parallel transport of $u$ along $v$ $$ u_R^{//} \approx \left( u^k - \epsilon \Gamma_{ij}^k v^i u^j \right) \left( \frac{\partial}{\partial x^k} \right)_R \approx \left( u^k + O(\epsilon^2) \right) \left( \frac{\partial}{\partial x^k} \right)_P $$ Which I reported in the tangent space of $P$, using the fact that \begin{equation} \left( \frac{\partial}{\partial x^k} \right)_R = \left( \frac{\partial}{\partial x^k} \right)_P + \epsilon v^i \Gamma_{ik}^j \left( \frac{\partial}{\partial x^j} \right)_P \end{equation} Now that my vectors all belong to the same tangent space $T_P M$ I can finally verify $$ u_R - u_R^{//} = \nabla_{v} u $$ If I want to get the Lie Bracket from the drawing, I can calculate the vectors $u_R$ and $v_Q$, report them in $P$ and combine them accordingly, i.e. \begin{equation} \begin{split} (u_P + v_Q) - (v_P + u_R) &= u^k + v^k + \epsilon v^i u^j \Gamma_{ij}^k + \epsilon v^i \frac{\partial u^k}{\partial x^i} - \left( u^k + v^k + \epsilon u^i v^j \Gamma_{ij}^k + \epsilon u^i \frac{\partial v^k}{\partial x^i} \right) \\ &= \epsilon v^i u^j T_{ij}^k - \epsilon [u,v] \end{split} \end{equation} So also the torsion appears to me in that subtraction, and that is why I cannot understand that picture... What am I missing? It seems to me that I should not report the vectors back in P, but then how can I add or subtract vectors in different tangent spaces?

And once this is solved, what is the connection of the Lie Bracket with the Torsion, could anybody shine light on this?

Answer 1

Lie bracket of two vector fields, $[u,v]$, measures how is the gap when we try to draw a rectangle along flow lines of $u$ and $v$. Let' see:

Let's go to a local chart $U$ with coordinates $x_i$. If $u=u^i \partial x_i$ and $v=v^i \partial x_i$ we have that $$ [u,v]=\left( u^j \frac{\partial v^i}{\partial x_j}- v^j \frac{\partial u^i}{\partial x_j} \right) \partial x_i $$

On the other hand, consider a point $P$, in the local chart. Let's call $\varphi$ to the flow of $v$ and $\phi$ to the flow of $u$. If we move a little amount $\epsilon$ from $P$ following $v$ we arrive to a point $R$ that can be approximated by: $$ \varphi_P(\epsilon)=R=P+\epsilon v_p+O(\epsilon^2) $$

Let's call $R'=P+\epsilon v_p$. Now we can move along the flow of $u$. If we moved from $R$ we would arrive to, say, $S$ (the perfect final position), but if we begin in $R'$ we will arrive to $S'$. But since we are approximating, we actually arrive to a certain $S''$ in the following way: $$ \phi_{R'}(\epsilon)=S'=R'+\epsilon u_{R'}+O(\epsilon^2) $$ where we take $S''=R'+\epsilon u_{R'}$

But observe that

$$ S''=P+\epsilon v_P+\epsilon\left(u_P+\epsilon\frac{\partial u^i_P}{\partial x_j} v^j_P+O(\epsilon^2) \right)=P+\epsilon v_P+\epsilon u_P+\epsilon^2 \frac{\partial u^i_P}{\partial x_j} v^j_P+O(\epsilon^3) $$

If we begin our whole ``approximated'' journey from $P$ but beginning with the flow of $u$ instead, we would arrive to a certain $T''$, such that: $$ T''=P+\epsilon u_P+\epsilon v_P+\epsilon^2 \frac{\partial v^i_P}{\partial x_j} u^j_P+O(\epsilon^3) $$

So the vector $T''-S''$ (remember we are in a local chart) is $$ T''-S''=\epsilon^2[u,v]_P+O(\epsilon^3) $$

So $[u,v]$ measures the failure to close a paralelogram, in some sense.

Here is a picture from TRTR, by Penrose.

But now, what about torsion? Given a connection on a manifold, $(M,\nabla)$, we can define a tensor named torsion as $$ T (u, v)= \nabla_u v- \nabla_v u-[u,v] $$

Since $[u,v]$ measures the fail to close a rectangle along flow lines of $u$ and $v$, $T (u, v)$ measures the fail to close a rectangle made of parallel transported vectors along the flow, as you can observe in the picture you posted

So, to sum up, Lie bracket tells you if the vector fields have some "compatibility": their flows yield closed paralelograms when you move equal quantities in them ($\epsilon$).

The torsion, instead, tells you something about the underlying geometry of the manifold: even two "compatible" (in the sense above) vector fields may not close when they are parallel transported along each other. But if the connection IS TORSION FREE, two vector fields such that one is parallel along the flow of the other one will be "compatible".