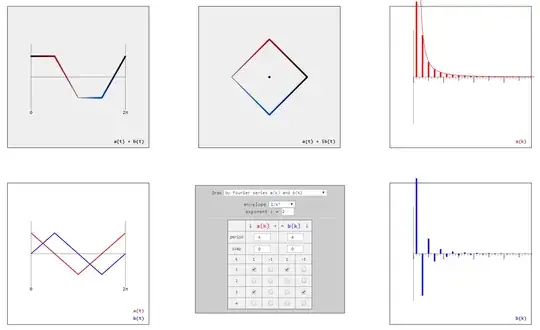
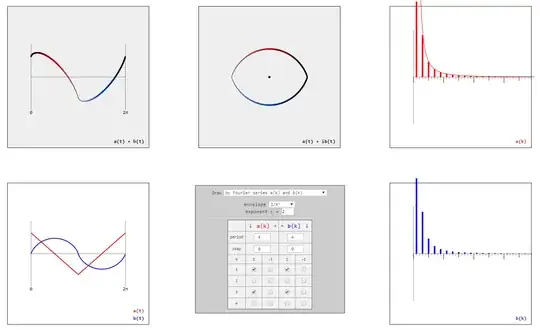
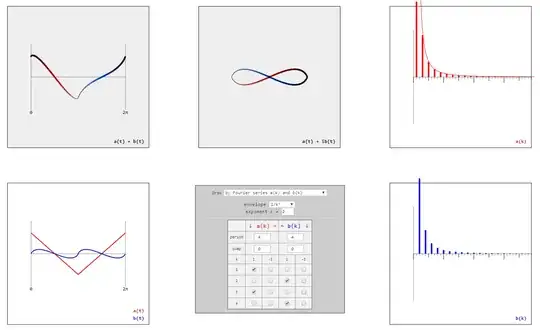
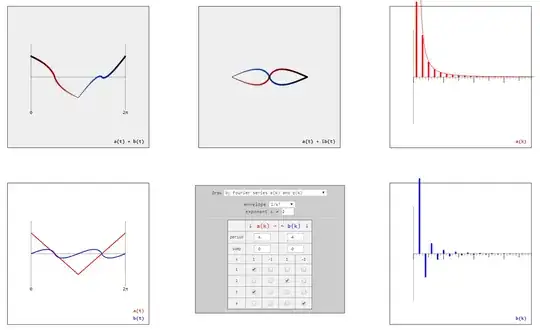
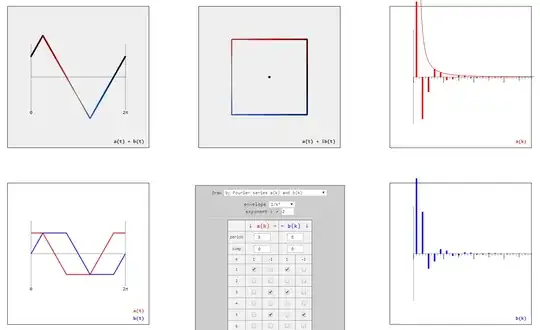
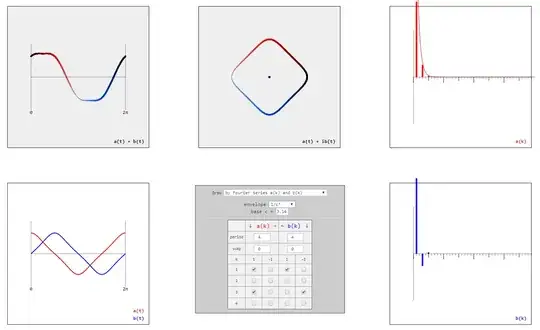
Consider two types of parametrized curves $\gamma:[0,2\pi]\rightarrow \mathbb{R}^2$
open curves $\gamma_\sim(t) = (t,a(t) + b(t))$
closed curves $\gamma_\bigcirc(t) = (a(t),b(t)) = a(t) + ib(t)$
with $a(t)$, $b(t)$ being $2\pi$-periodic functions, i.e. $a(0) = a(2\pi)$ and $b(0) = b(2\pi)$.
These curves – considered as geometric shapes – have some properties, for example:
symmetries (rotational and others)
number of singularities (where the curve goes to infinity)
number of vertices (where the curve is not smooth)
number of straight edges
being convex
number of self-intersection points (only for closed curves)
As a periodic function, $a(t) + b(t)$ has Fourier series
$$a_k = \int_0^{2\pi}(a(t)+b(t))\cos(kt)\mathrm{d}t$$
$$b_k = \int_0^{2\pi}(a(t)+b(t))\sin(kt)\mathrm{d}t$$
For the sake of simplicity consider only such $a(t)$, $b(t)$ with
$$a(t) = \sum_{k=0}^\infty a_k\cos(kt)$$
$$b(t) = \sum_{k=0}^\infty b_k\sin(kt)$$
(constant factors omitted), i.e. $a(t)$ being an even function and $b(t)$ being an odd function.
The Fourier series $a_k$, $b_k$ have some properties, too, for example
having an envelope of shape $k^{-c}$ or $c^{-k}$ for some $c\geq 1$
a periodic pattern by which the signs of $a_k$, $b_k$ change between $+1$, $0$ and $-1$
$a_k$ and $b_k$ having the same envelope
$a_k$ and $b_k$ having equal or shifted periodic patterns
Sticking to these sets of properties (of shapes and Fourier series) one may ask:
How do these properties relate, and what can be told about a shape knowing the properties of its Fourier series and vice versa?
Here is just one relation that I already have found:
The Fourier series
$$a_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod n \\ +k^{-2} & \text{ for } k \equiv (n-1) \pmod n\\ 0 & \text{ otherwise } \end{cases}$$
$$b_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod n\\ -k^{-2} & \text{ for } k \equiv (n-1) \pmod n\\ 0 & \text{ otherwise } \end{cases}$$
give rise to a regular $n$-gon (with all its symmetries, vertices, and straight edges).
My question (which is a big-list question of sort) asks for more examples, preferrably "simple" and otherwise "astonishing" ones.
Going one step further: How are relations between the Fourier series of two different shapes reflected in relations between the two shapes (the one being a rotation, homeomorphic distortion or other transformation of the other) and vice versa?
Again I have found a specific example:
The Fourier series
$$a_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod {2n} \\ -k^{-2} & \text{ for } k \equiv (n-1) \pmod {2n}\\ -k^{-2} & \text{ for } k \equiv (n+1) \pmod {2n}\\ +k^{-2} & \text{ for } k \equiv (2n-1) \pmod {2n}\\ 0 & \text{ otherwise } \end{cases}$$
$$b_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod {2n} \\ +k^{-2} & \text{ for } k \equiv (n-1) \pmod {2n}\\ -k^{-2} & \text{ for } k \equiv (n+1) \pmod {2n}\\ -k^{-2} & \text{ for } k \equiv (2n-1) \pmod {2n} \\ 0 & \text{ otherwise } \end{cases}$$
give rise to a regular $n$-gon rotated by $\pi/n$.
And then this one:
The Fourier series
$$a_k = \begin{cases} +\gamma^{-k} & \text{ for } k \equiv 1 \pmod 4 \\ +\gamma^{-k} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$
$$b_k = \begin{cases} +\gamma^{-k} & \text{ for } k \equiv 1 \pmod 4\\ -\gamma^{-k} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$
with $\gamma = \sqrt{2+2\sqrt{3}+\sqrt{15+8\sqrt{3}}}=3.291795...$ gives rise to a square with rounded corners.
Further examples are welcome.
I wrote a little tool to play around with Fourier series and compare them with the shapes they give rise to. The following gallery shows by some simple examples what can be done and observed with it. If you are interested in using it by yourself, just drop me an email.
[There is a follow-up question to this one: The number $\pi$ in an unexpected context.]
Edit: I would guess the following is true.
The shape $\gamma_\bigcirc(t)=(a(t),b(t))$ defined by the series $a_k$, $b_k$ is symmetric with respect to the y-axis iff $a_k, b_k = 0$ for even $k$.
In this case $\gamma_\sim(t) = (t,a(t)+b(t))$ is an odd function, i.e. invariant under rotation by $\pi$ around the point $(\frac{\pi}{2},0)$.