18

[This is a follow-up question to this one: Figures and Numbers: Relating properties of geometric shapes and their Fourier series.]

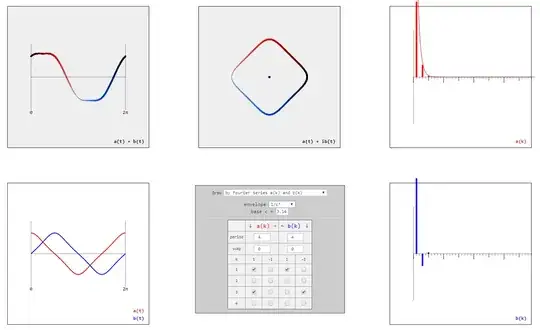
Drawing shapes by some predefined Fourier series I found this square with rounded corners which is given by the Fourier series

$$a_k = \begin{cases} +\pi^{-k} & \text{ for } k \equiv 1 \pmod 4 \\ +\pi^{-k} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$

$$b_k = \begin{cases} +\pi^{-k} & \text{ for } k \equiv 1 \pmod 4\\ -\pi^{-k} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$

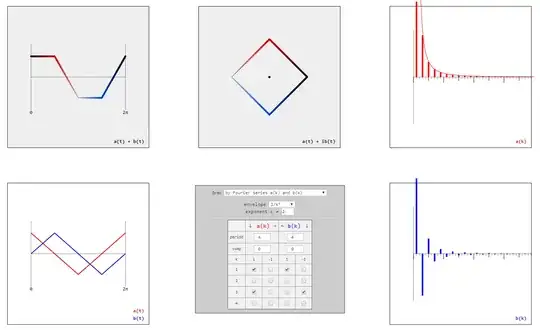
enter image description here

Compare this to the perfect square given by

$$a_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod 4 \\ +k^{-2} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$

$$b_k = \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod 4\\ -k^{-2} & \text{ for } k \equiv 3 \pmod 4\\ 0 & \text{ otherwise } \end{cases}$$

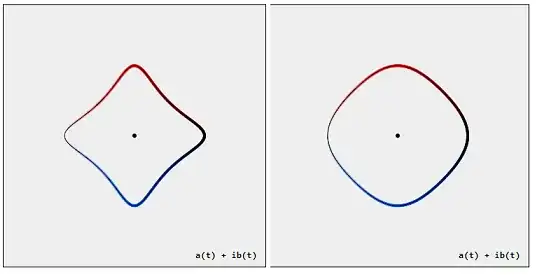
enter image description here

Note that for bases different from $\pi$ in the formulas for $a_k$ and $b_k$, the rounded square hasn't got so "straight" sides anymore, e.g. for base $2.5$ and $4.5$:

enter image description here

My question is:

Might it be true, that for base $\pi$ in the formulas for $a_k$, $b_k$ above, the resulting shape has "maximally straight" sides? And if so: How to prove it?

First, of course, one has to define what "maximally straight" means.

For the sake of comparison here is the unrounded square with exponents $1.5$ and $2.5$ instead of $2$ in the corresponding formulas. As in the case of the rounded square, $2$ (instead of $\pi$) yields the "maximally straight" sides.

enter image description here

Hans-Peter Stricker
  • 18,159
  • 4
    I guess maximally straight could mean that $\pi$ is the largest base such that the resulting shape is convex. Whether that's true I don't know – Bananach Apr 06 '19 at 08:20
  • @Banach: Great idea! This might make the question answerable. – Hans-Peter Stricker Apr 06 '19 at 08:21
  • 2
    @Banach: I guess you mean the smallest base such that the resulting shape is convex. – Hans-Peter Stricker Apr 06 '19 at 08:22
  • 1
    Yes, I do. And since we are only interested in the sign of the curvature, which is equal to that of $x'y''-x''y'$, this might actually be feasible – Bananach Apr 06 '19 at 08:48
  • 1
    @Banach: Do you plan to give it a try? – Hans-Peter Stricker Apr 06 '19 at 08:50
  • @Banach: The same proof will show that $2$ is an distinguished number in the case of the unrounded square (see my edit above): It's the smallest exponent such that the resulting shape is convex. (The interchangable roles of "base" and "exponent" is the interesting point, I find.) – – Hans-Peter Stricker Apr 06 '19 at 10:55
  • 4
    It looks like $\pi$ doesn't give a convex shape, one can visually check that the line $y=x+0.40065$ cuts the shape in four points, so the shape's "sides" bend inwards. Following Bananach's approach and setting the curvature $K(a,t)$ to zero at $t=\pi/4$, and if WolframAlpha is not mistaken, it seems that the minimum such number is actually $a=\sqrt{2+2\sqrt{3}+\sqrt{15+8\sqrt{3}}} = 3.291795...$, the greatest positive solution to $a^{10}-9a^8-22a^6+22a^4+9a^2-1=0$. – pregunton Apr 06 '19 at 14:05
  • 1
    @pregunton: What a pity! Thanks anyway. – Hans-Peter Stricker Apr 06 '19 at 14:27

0 Answers0