Linearizing the trigonometric functions or: Squaring the circle by Fourier transformation

Question

It's an easy exercise to approximate the cosine and the sine function by a piecewise linear function on the unit interval $[0,1]$. Let $\tau = 2\pi$.

Let

$$\boxed{\cos_\bigcirc(x) = \cos(\tau x)\\\sin_\bigcirc(x) = \sin(\tau x)}$$

and compare this to

$$\boxed{\cos_\square(x) = \begin{cases} +1 & \text{ for } \frac{0}{8} \leq x \leq \frac{1}{8} \\ +2 - 8x & \text{ for } \frac{1}{8} \leq x \leq \frac{3}{8} \\ -1 & \text{ for } \frac{3}{8} \leq x \leq \frac{5}{8} \\ -6 + 8x & \text{ for } \frac{5}{8} \leq x \leq \frac{7}{8} \\ +1 & \text{ for } \frac{7}{8} \leq x \leq \frac{8}{8} \\ \end{cases} \\ \\\sin_\square(x) = \begin{cases} +0 + 8x & \text{ for } \frac{0}{8} \leq x \leq \frac{1}{8} \\ +1 & \text{ for } \frac{1}{8} \leq x \leq \frac{3}{8} \\ +4 - 8x & \text{ for } \frac{3}{8} \leq x \leq \frac{5}{8} \\ -1 & \text{ for } \frac{5}{8} \leq x \leq \frac{7}{8} \\ -8 + 8x & \text{ for } \frac{7}{8} \leq x \leq \frac{8}{8} \\ \end{cases}}$$

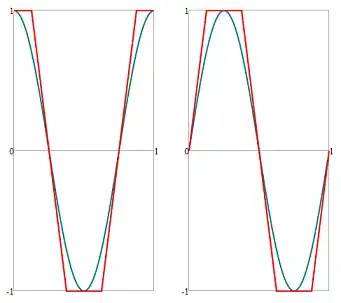
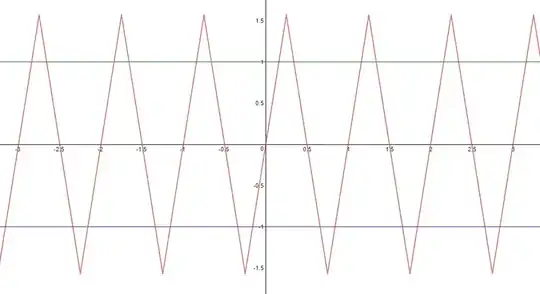
These are the plots:

Observations

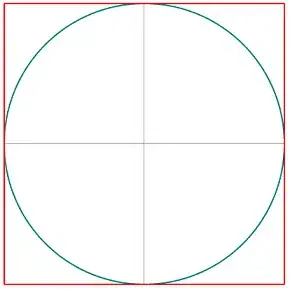
• It may come as a surprise or not that while $\cos_\bigcirc(x)$ and $\sin_\bigcirc(x)$ yield the unit circle by $x_\bigcirc(x) = \cos_\bigcirc(x)$ and $y_\bigcirc(x) = \sin_\bigcirc(x)$, the functions $\cos_\square(x)$ and $\sin_\square(x)$ yield the unit square by $x_\square(x) = \cos_\square(x)$ and $y_\square(x) = \sin_\square(x)$. By "unit square" I mean the square with "radius" $1$, not with side length $1$. The unit circle in the incircle of this square:

• While the circumference of the unit circle is just the "number of the circle" $\tau$, the circumference of the unit square is $8$ (the "number of the square"). Note how $8$ is used in the definition of $\cos_\square(x)$ and $\sin_\square(x)$, compared to $\tau$ in the definition of $\cos_\bigcirc(x)$ and $\sin_\bigcirc(x)$. Note further that not by accident $8 \approx \tau$ and that not by accident $8 = 3^2 - 1^2$:

• There are natural generalizations of piecewise linear approximations of the cosine and the sine for arbitrary regular $n$-polygons which will approximate the true functions better and better as the polygons will approximate the circle better and better.

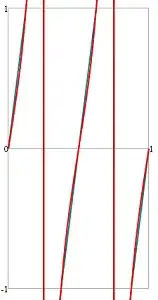
• The tangens $\tan_\bigcirc(x) = \tan(\tau x)$ is very well approximated already by $\tan_\square(x) = \frac{\sin_\square(x)}{\cos_\square(x)}$:

• The functions $\cos_\square(x)$ and $\sin_\square(x)$ can be used to parametrize the square spiral analoguous to how $\cos_\bigcirc(x)$ and $\sin_\bigcirc(x)$ can be used to parametrize the Archimedean spiral.

Questions

1. Under which name and in which contexts have the functions $\cos_\square(x)$ and $\sin_\square(x)$ been studied before?
2. Is there an elegant and/or more compact way to write the equations for $\cos_\square(x)$ and $\sin_\square(x)$ in one closed expression, e.g. by using the Heaviside function?
3. Is there a closed formula for the Fourier transform of $\cos_\square(x)$ and $\sin_\square(x)$ (the "Fourier transform of the quadrature of the circle")?

This is how the Fourier transforms of $\cos_\square(x)$ and $\sin_\square(x)$ look like:

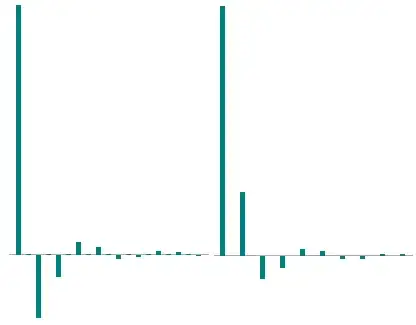
Summary

Thanks to user J.M. we now know the Fourier coefficients $\widehat{\cos}_\square(k)$

$$\boxed{\widehat{\cos}_\square(k) = 8 \cdot \begin{cases} \ \ \ \ \ 0 & \text{ for } k \equiv 0 \mod 2 \\ +(\pi k)^{-2} & \text{ for } k \equiv 1 \mod 8 \text{ or } k \equiv 7 \mod 8\\ -(\pi k)^{-2} & \text{ for } k \equiv 3 \mod 8 \text{ or } k \equiv 5 \mod 8\\ \end{cases}}$$

and $\widehat{\sin}_\square(k)$ accordingly.

Now can perform the squaring of the circle by these steps:

1. Consider $\cos_\bigcirc(x)$ and $\sin_\bigcirc(x)$ which "draw" the unit circle (with diameter $2$).

2. Consider the functions $\cos_\square(x)$ and $\sin_\square(x)$ defined by

$$\cos_\square(x) := \sum_{k=0}^{\infty} \widehat{\cos}_\square(k)\cos_\bigcirc(kx)\\ \sin_\square(x) := \sum_{k=0}^{\infty} \widehat{\sin}_\square(k)\sin_\bigcirc(kx)$$

3. The functions $\cos_\square(x)$ and $\sin_\square(x)$ "draw" the unit square (with diameter $2$).

Answer 1

For #2, we can do this via floor, absolute value, min, and max.

First, we need a triangle wave. $\left|x - \left\lfloor x \right\rfloor - 1/2\right|$ gives a triangle wave of period $1$ and range $[0,1/2]$. We need range $[-2,2]$ because that's where the diagonals will meet, so multiply by $8$ and subtract $2$: $8\left|x - \left\lfloor x \right\rfloor - 1/2\right|-2$. Then we cut off the top and bottom with min and max:

$$\cos_\square(x) = \min\left(\max\left(-1,8\left|x - \left\lfloor x \right\rfloor - 1/2\right|-2\right),1\right)$$

THen since $\sin_\square(x)=\cos_\square\left(x-\frac{1}{4}\right)$ we can just ... do that and get

$$\sin_\square(x) = \min\left(\max\left(-1,8\left|x - \left\lfloor x-1/4 \right\rfloor - 3/4\right|-2\right),1\right)$$

Answer 2

The work has been done by user J.M. (who seems to be a mathematician of sorts), so let me just put it in order.

First let me rewrite the definition of $\cos_\square(x)$ a bit:

$$\cos_\square(x) = \begin{cases} +1 & \text{ for } -1 \leq 8x \leq 1 \\ +2 - 8x & \text{ for }\ \ \ \ \ 1 \leq 8x \leq 3 \\ -1 & \text{ for }\ \ \ \ \ 3 \leq 8x \leq 5 \\ -6 + 8x & \text{ for }\ \ \ \ \ 5 \leq 8x \leq7 \\ \end{cases}$$

The unit square has diagonal (= "diameter") $2\sqrt{2}$, so let's normalize $\cos_\square(x)$ by a factor $\frac{1}{\sqrt{2}}$ so the unit square has diameter $2$ (just like the unit circle has diameter $2$):

$$\boxed{\cos_\square(x) = \frac{1}{\sqrt{2}}\cdot\begin{cases} +1 & \text{ for } -1 \leq 8x \leq 1 \\ +2 - 8x & \text{ for }\ \ \ \ \ 1 \leq 8x \leq 3 \\ -1 & \text{ for }\ \ \ \ \ 3 \leq 8x \leq 5 \\ -6 + 8x & \text{ for }\ \ \ \ \ 5 \leq 8x \leq7 \\ \end{cases}}$$

User J.M.'s expression for the Fourier coefficients $\widehat{\cos}_\square(k)$ can then be written in this form:

$$\boxed{\widehat{\cos}_\square(k) = 8 \cdot \begin{cases} \ \ \ \ \ 0 & \text{ for } k \equiv 0 \mod 2 \\ +(\pi k)^{-2} & \text{ for } k \equiv 1 \mod 8 \text{ or } k \equiv 7 \mod 8\\ -(\pi k)^{-2} & \text{ for } k \equiv 3 \mod 8 \text{ or } k \equiv 5 \mod 8\\ \end{cases}}$$

Answer 3

To those who don't have the function $f(x) = \arcsin(\sin(2\pi x))$ before their inner eye, this is how it looks like:

It's essentially this function that user J.M. cuts off at $\min = -1$ and $\max = +1$ to yield $\sin_\square(x)$.