Fourier series of regular polygons

Question

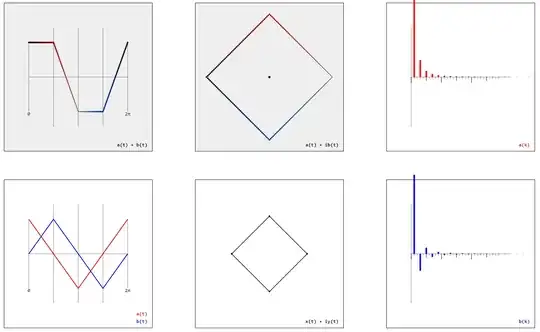
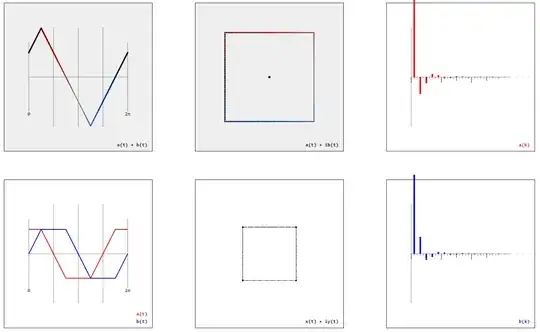
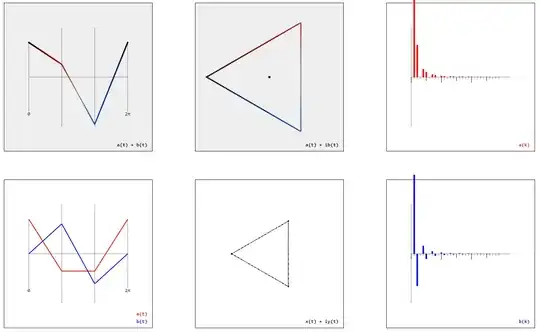
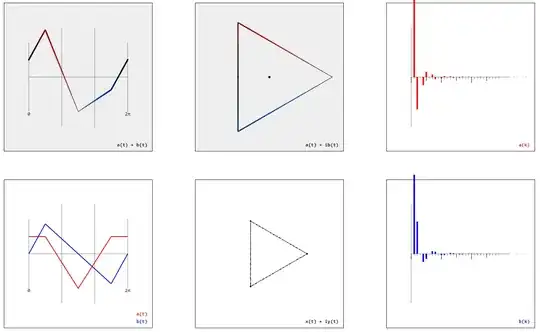
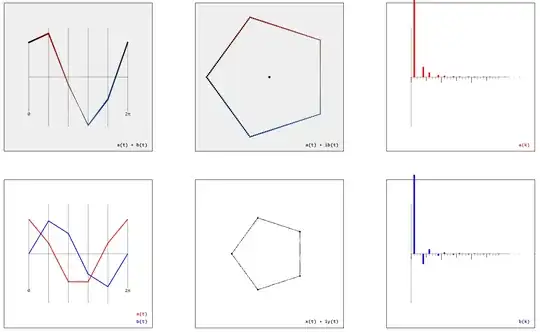
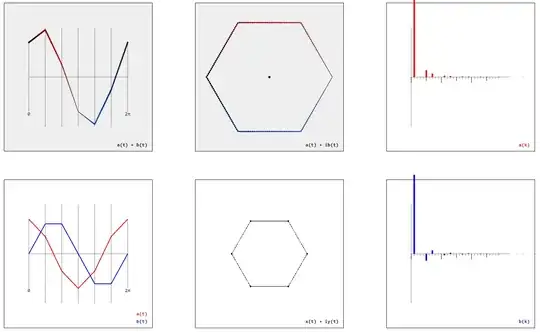
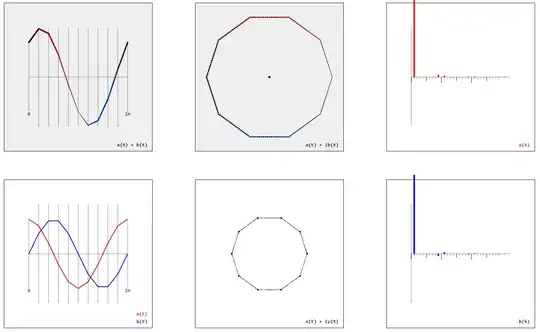
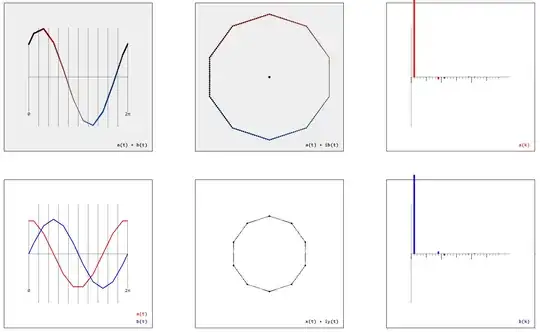
The definition of a regular polygon by two real-valued functions $(x(t)$, $y(t))$ – or alternatively by a complex-valued function $x(t) + iy(t)$ – suggests to calculate the Fourier series $a_k$, $b_k$ by

$$a_k \sim \int_0^{2\pi}(x(t)+y(t))\cos(kt)\mathrm{d}t$$

$$b_k \sim \int_0^{2\pi}(x(t)+y(t))\sin(kt)\mathrm{d}t$$

Not surprisingly the two functions

$$a(t) \sim \sum_{k=0}^\infty a_k\cos(kt)$$

$$b(t) \sim \sum_{k=0}^\infty b_k\sin(kt)$$

are linearized approximations of the cosine and sine function (very much like the regular polygons are linearized approximations of the circle):

Rotating the $n$-gon by $\frac{\pi}{n}$ yields another figure with another Fourier series and with another linearized approximation of the cosine and sine function:

For the rotated square, I already know an explicit formula for $a_k$ - thanks to user J.M.'s comment on another question:

$$a^{(4)}_k(\pi/4) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \mod 8 \text{ or } k \equiv 7 \mod 8\\ -k^{-2} & \text{ for } k \equiv 3 \mod 8 \text{ or } k \equiv 5 \mod 8\\ 0 & \text{ otherwise } \end{cases}$$

and I guess it's a rather straight forward exercise to generalize this for arbitrary $n$-gons. Nevertheless I didn't manage to find a concise closed formula for $a^{(n)}_k(\alpha)$, $\alpha = 0,\pi/n$.

Question 1: Can someone give a closed formula for $a^{(n)}_k(\alpha)$, $\alpha = 0,\pi/n$?

(I assume this formula will only contain $k^{-2}$ terms. So it's more about the period length, positions of the zeros, and the alternation of the signs. Note that the smallest $k>1$ with $a^{(n)}_k, b^{(n)}_k \neq 0$ is just $k = n-1$, see the gallery below.)

Three other questions I have:

Question 2: How does $a^{(n)}_k(\alpha)$ look like for arbitrary rotation angles – not just $\alpha = \pi/n$?

Question 3: Does it make sense to ask for something like a "convolution" $c^{(n)}_k(\alpha)$ that takes the series $a^{(n)}_k(0)$ to the series $a^{(n)}_k(\alpha)$ by

$$a^{(n)}_k(\alpha) = \sum_{m=0}^\infty a^{(n)}_m(0)c^{(n)}_{k-m}(\alpha)$$

If so: What would $c^{(n)}_k(\alpha)$ look like?

Question 4: Is the exponent $2$ in $k^{-2}$ just a coincidence or is it by deeper reasons the dimension of the plane?

---

Gallery

Answer 1

Let me try to answer Question 1.

Observing that

• the smallest $k>1$ with $a^{(n)}_k \neq 0$ is just $n-1$

• the next one is $n+1$

• there is a period of length $n$

(see the gallery) I would guess that the formula for $a^{(n)}_k(0)$ is

$$\boxed{a^{(n)}_k(0) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod n \\ +k^{-2} & \text{ for } k \equiv (n-1) \pmod n\\ 0 & \text{ otherwise } \end{cases}}$$

For $b^{(n)}_k(0)$ we would have

$$\boxed{b^{(n)}_k(0) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod n\\ -k^{-2} & \text{ for } k \equiv (n-1) \pmod n\\ 0 & \text{ otherwise } \end{cases}}$$

Generalizing the result for $a^{(4)}_k(\pi/4)$

$$a^{(4)}_k(\pi/4) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod 8 \text{ or } k \equiv 7 \pmod 8\\ -k^{-2} & \text{ for } k \equiv 3 \pmod 8 \text{ or } k \equiv 5 \pmod 8\\ 0 & \text{ otherwise } \end{cases}$$

I would guess that the general formula is something like

$$\boxed{a^{(n)}_k(\pi/n) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod {2n} \text{ or } k \equiv (2n-1) \pmod {2n}\\ -k^{-2} & \text{ for } k \equiv (n-1) \pmod {2n} \text{ or } k \equiv (n+1) \pmod {2n}\\ 0 & \text{ otherwise } \end{cases}}$$

and accordingly

$$\boxed{b^{(n)}_k(\pi/n) \sim \begin{cases} +k^{-2} & \text{ for } k \equiv 1 \pmod {2n} \text{ or } k \equiv (n-1) \pmod {2n}\\ -k^{-2} & \text{ for } k \equiv (2n-1) \pmod {2n} \text{ or } k \equiv (n+1) \pmod {2n}\\ 0 & \text{ otherwise } \end{cases}}$$

A similar question as my Question 4 in the original post remains:

Is the factor $2$ in $(2n-1)$ and $\mathrm{mod}\ 2n$ just a coincidence, or is it related to the exponent $2$ in $k^{-2}$ and the dimension of the plane – or to the difference between $n-1$ and $n+1$?

(Probably not: It most probably comes from the fact that we divided the angle $2\pi/n$ by exactly $2$ to get $\alpha = \pi/n$.)