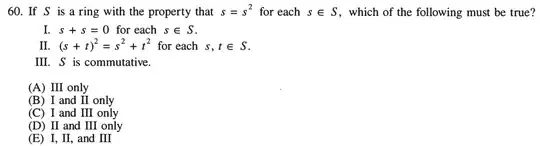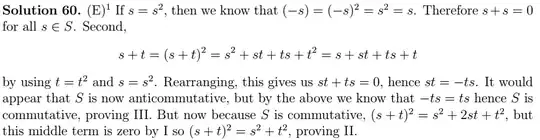GRE 9768 #60 1. Does $(s+t)^2=s^2+t^2$ imply $s+s=0$? 2. Idempotent matrices do not form a ring?

Question

GRE 9768 #60 on what appears to be Boolean rings:

Ian Coley's approach is to prove $(I)$ and $(I) \implies (II) \implies (III)$

---

1. I think $(II) \implies (I)$. My attempt:

$$(s+t)^2=s^2+t^2 \iff s^2+st+ts+t^2=s^2+t^2 \iff st + ts = 0$$

By choosing $t=1$, we get $s+s=0$.

• Is this flawed because actually rings don't necessarily contain $1$ even though Algebra by Michael Artin defines that they do?

• What counterexamples does $(II) \implies (I)$ have if rings don't necessarily contain $1$ please? If none, then please prove $(II) \implies (I)$ for rings that don't necessarily contain $(1)$.

---

2. Am I right to say that collecting all idempotent matrices in $\mathbb R^{n \times n}$ does not form a ring $R$ because if such collection were a ring, then it would be a Boolean ring and thus imply $A+A=0$ for all $A$ in $R$ which would imply $A=0$?

Answer 1

1. From comments here: How do I know the definition of rings or of anything on the GRE given that definitions can vary?

For the question about Boolean rings, this has been left unspecified, but a correct answer to the question will not need to assume the ring has a unit. – Joppy

2. From comments here: GRE 9768 #60 Boolean rings: 1. Does $(s+t)^2=s^2+t^2$ imply $s+s=0$? 2. Idempotent matrices do not form a ring?

The sum of two idempotent matrices may not be idempotent, for example double an idempotent matrix. – Joppy

@Joppy Right thanks, but in that case, we can view question 2 as about a different way of proving then, I guess. – BCLC

I guess? But whenever you collect a subset of stuff together and want to call it a ring, the most obvious things to check are closure under addition and multiplication. – Joppy

@Joppy Lol thanks. I'm inelegant. XD Post as answer? ^-^ – BCLC 49 mins ago