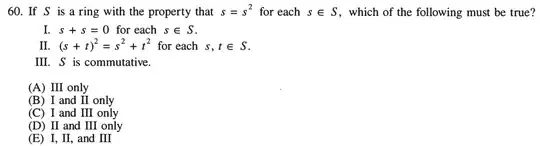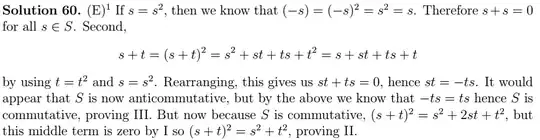GRE 9768 #60 Boolean non-commutative rings: Prove $(-s)^2=s^2$ without commutativity.

Question

GRE 9768 #60

Ian Coley's approach is to prove $(I)$ and $(I) \implies (II) \implies (III)$

In proving $(I)$, how do we prove $$(-s)^2=s^2$$ without commutativity (but with $s=s^2$, if need be, and of course without $s+s=0$)?

Attempt 1:

$$-s=(-s)^2=(-s)(-s)\stackrel{(*)}{=}(-1)(s)(-1)(s)$$

$$s=(s)^2=(s)(s)$$

I'm stuck. Perhaps $-1$ commutes with every element of a ring assuming that the ring has a multiplicative identity $1$, but if the ring doesn't have a $1$, then I guess the ring has $-1$ only vacuously and therefore $(*)$ is meaningless.

Attempt 2:

$$-s=(-s)^2=(-s)(-s)$$

$$s=(s)^2=(s)(s)$$

$$\implies 0=s-s=s^2 + (-s)^2 \implies s^2 = -(-s)^2$$

I'm stuck.

Attempt 3:

$$-s=(-s)^2=(-s)(-s)$$

$$s=(s)^2=(s)(s)$$

$$\implies -s = -(s)^2=-(s)(s)$$

$$\implies (-s)(-s)=-(s)(s)$$

I'm stuck.

Answer 1

$-s$ is the additive inverse of $s$, so $s+(-s)=0$. Then $$0=s0=s(s+(-s))=s^2+s(-s).$$ Also $$0=0(-s)=(s+(-s))(-s)=s(-s)+(-s)^2.$$ Therefore $s^2$ and $(-s)^2$ are both the inverse of $s(-s)$ in the commutative group of $R$ under addition: $s^2=(-s)^2$.

But, a better approach to I, is to note that in addition to $s^2=s$ we also have $(s+s)^2=s+s$, that is $s^2+s^2+s^2+s^2=s+s$. Then $s+s+s+s=s+s$ and cancelling $s+s$ in the Abelian group of $R$ under addition gives $s+s=0$.