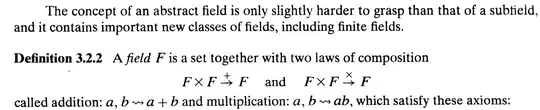0

Algebra by Michael Artin Ch3, Ch11

Artin has different definitions of rings particularly that his rings are commutative in both addition and multiplication. Based on his definitions, (*) I believe that $0$ is in subrings for the same reason $0$ is in subfields: (**) $$1-1=0$$

Am I mistaken?

(*)

Definition of a subring of the ring of complex numbers $\mathbb C$ (and then I guess this is extended to a subring of a ring $R$)

enter image description here

Definition of a ring

enter image description here

(**)

Earlier, subfields of the field $\mathbb C$, fields and subfields of fields were defined similarly.

Definition of a subfields of the field of complex numbers $\mathbb C$ (and then I guess this is extended to a subfield of a field $F$)

enter image description here

Definition of a field

enter image description here

enter image description here

Community
  • 1
BCLC
  • 13,459
  • 3
    By every definition I've ever heard, a subring contains $0$ (the additive identity). You're correct in saying that it is implied by closure under subtraction and inclusion of the element $1$, but alternatively we know that subrings are rings in their own right, and every ring has an underlying additive abelian group (which requires the existence of an identity element, $0$) – Theo C. Oct 23 '18 at 02:43
  • @D.Beec Thanks! So, we could actually say to Artin that 'that subfields are fields in their own right' is an alternative proof than '$1-1=0$' to show $0$ is in every subfield? Hmmm....I mean, that $0$ is in every subfield sounds like part of the proof of showing that every subfield is a field. So, how would you show that every subfield is a field without using $1-1=0$ to show $0$ is in every subfield? – BCLC Oct 23 '18 at 02:48
  • 1
    Here's an alternative way to consider it: Let $F$ be a field with the given operations of $+$ and $\times$. We call $A$ a subfield of $F$ if $A\subseteq F$ and if $A$ is a field with respect to the same operations $+$ and $\times$. Now, in 3.2.1 Artin is trying to provide a minimal set of properties that if true, show that $A$ is indeed a subfield of $F$. In this list, he doesn't explicitly state "$A$ must contain the additive identity", but that property is implied by this list. He's trying to keep the list short so if you ever have to check for a subfield, you can do it quickly – Theo C. Oct 23 '18 at 03:02

1 Answers1

3

Subrings contain $0$ because they are, in particular, groups (written additively). Recall that a ring is a group written additively with a mutliplicative structure. So, not all rings have 1 but all rings have 0 since that is the identity element in the underlying group.

So, why does a subring contain 0? Because it is a ring and so, in particular, an abelian group written additively. Hence, contains an identity which in this case would be 0.

RhythmInk
  • 3,032
  • 2
    It is slightly more subtle than that. Consider that if we don't explicitly require a subring to contain $1$, then the subring may still contain a multiplicative identity that works in that subring. For example $\mathbb Z/6\mathbb Z$ could have ${0,3}$ as a subring, with $3$ filling the role of the multiplicative identity. This situation cannot arise for additive identities because a ring is an additive group. In a group the equation $a+a=a$ characterizes the identity uniquely, and therefore the subring's $0$ must necessarily equal the $0$ of the larger ring. – hmakholm left over Monica Oct 23 '18 at 02:54
  • 1
    Thanks for point that out. I should have been more specific. It seemed OP was asking about why they contained 0 conceptually not as the distinguished element so I was a little careless. – RhythmInk Oct 23 '18 at 02:56
  • Thanks RhythmInk and @Henning Makholm! Turns out I might be pretty screwed for the GRE because Artin defines rings to include $1$. – BCLC Oct 23 '18 at 03:08
  • 1
    Most folks do. What you will encounter on the GRE will very likely be rings with unity. In the most general case, a ring not have a multiplicative identity, but most folks only bother considering rings with unity in their texts. I would suggest looking at Pinter's introduction to abstract algebra as well. A more basic text that'll help with intuition. Feel free to send me a message if you would like to chat more about this kind of thing. – RhythmInk Oct 23 '18 at 03:10
  • 1
    @BCLC please accept the answer if your question is answered – RhythmInk Oct 23 '18 at 03:40
  • RhythmInk About definitions, may you please help here? – BCLC Oct 23 '18 at 03:41
  • Wait this one: How do I know the definition of rings or of anything on the GRE given that definitions can vary? – BCLC Oct 23 '18 at 03:57