How to combine complex powers?

Question

Regarding this thread,

it is not possible to combine complex powers in the usual way:

$$ (x^y)^z = x^{yz} $$

There was mention of multi-valued functions, is there some theory that makes this all work out correctly?

Answer 1

For complex numbers the general way of defining $x^y$ (with $x$ nonzero) is as $\exp(ly)$ where $l$ is one of the logarithms of $x$. But $x$ does not have a unique logarithm, it has many. If $l$ is one logarithm of $x$ then the general one is $l+2n\pi i$ with $n$ an integer. Hence the general value of $x^y$ is $$\exp(ly+2\pi iny)=\exp(ly)\exp(2\pi i ny).$$

Before proceeding further note that if $y$ is an integer then $\exp(2\pi i ny)=1$ so that $x^n$ is uniquely determined. More generally if $y$ is a rational with denominator $d$ then $\exp(2\pi i ny)$ (and so $x^y$) takes $d$ different values. But if $y$ is irrational, then $x^y$ takes infinitely many variables.

In the problem in hand $x^y$ takes the values $\exp(ly)\exp(2\pi i ny)$ as above, and $x^{yz}$ the values $$\exp(lyz)\exp(2\pi inyz).$$ However in general each value of $x^y$ gives rise to infinitely many values of $(x^y)^z$, namely $$\exp((ly+2\pi iny)z+2\pi i mz)$$ so $(x^y)^z$ has a "doubly-infinite" family of values. In general, there will be values of $(x^y)^z$ which are not values of $x^{yz}$ so the "paradox" in the previous posting should be expected.

Answer 2

The original question asked about a theory that would make this all work out correctly. The previous answers are all correct, but they did not point out the underlying, unifying factor which makes all these computations much simpler: the Unwinding number. The unwinding number $\mathcal{K}(z)$ is defined to be $$ \ln(\exp(z)) = z + 2\pi i\mathcal{K}(z).$$ It is an integer which tells you how many times you need to 'unwind' $z$ before you get into the range where $\ln\circ \exp$ is the identity. This then allows a lot of identities to be 'fixed' with relative ease.

I also find the paper Reasoning about the Elementary Functions of Complex Analysis by Corless, Davenport, Jeffrey, Litt and Watt quite instructive in this domain.

Answer 3

Since people keep hearing about Riemann surfaces in the three threads thus far about complex exponentiation and the logarithm being multivalued, but are probably wondering about the multivalued part, here's a visualization courtesy of Michael Trott:

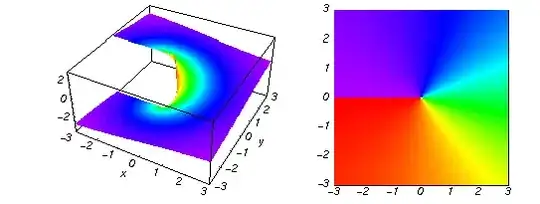
This is a plot of the logarithm's imaginary part over the complex plane. Note the branch cut running through the negative real axis. Analytic continuation consists of joining together copies of this cut surface above and below (corresponding to adding or subtracting integer multiples of $2\pi i$) and matching up the cuts of each piece to maintain continuity, thus:

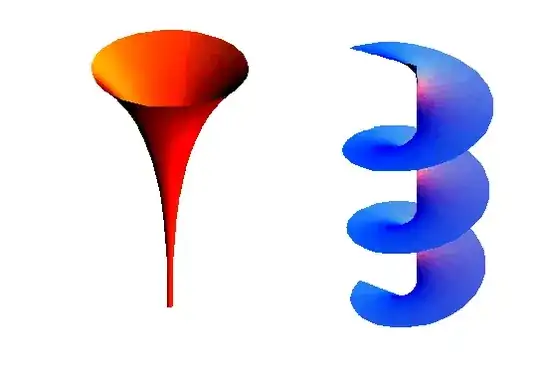
The surface on the right is the analytically continued imaginary part.

(images from here)

Answer 4

I guess the problem in general arises because $a^b$ can have multiple values. We have $$\begin{eqnarray} \log((x^y)^z) & = & z(\log(x^y)+2\pi im)=z(y(\log(x)+2 \pi in)+2\pi im)\\ & = & zy\log(x)+2\pi i(ny + m)z\\ & = & \log(x^{yz}e^{2\pi i(ny + m)z}) \end{eqnarray}$$

It seems a correction factor of $e^{2\pi i(ny + m)z}$ is necessary.

So all that can be said is that $\exists m,n\in\mathbb{Z}:(x^y)^z=x^{yz}e^{2\pi i(ny + m)z}$.

In particular, we can say that the correction term is 1 if $(ny+m)z$ is always an integer, which happens for example if we know $y,z\in\mathbb{Z}$.

Answer 5

One standard technique is that of Branches and Branch Cuts;

from the perspective that the multivaluedness of the log lies entirely in its

purely imaginary part, i.e., the argument of the number, and not in its real part.

In a sense, the $logz$ assigns to a number a polar representation $logz=ln|x|+iargz$,

but given a possible value for $argz$, $argz+k\pi$ also works, for any integer k,

which

leads to the multivaluedness. The key to multivaluedness is winding around the

origin. Every timea curve winds up around the origin, you end up with a new

possible and valid choice of argument, which gives you an additional representation

for that number.

This brings up the theory of branch cuts to help fix this and avoid multivaluedness;

a branch cut is a removal of a curve(s) from the plane so that the region that

remains after the removal prevents curves from winding around the origin and

so it eliminates the problem of multivaluedness.This is generalized to the case of

functions that depend on , or are defined in terms of, the log, like the square and

nth roots, and for regions other than the plane.