Stable strict local minimum implies local convexity

Question

Let $\bar{x}\in\mathbb{R}^n$ and $f:\mathbb{R}^n\rightarrow\mathbb{R}$ be a $C^2$ function.

We have known that if $\nabla f(\bar{x})=0$ and $\nabla^2f(\bar{x})>0$, i.e. $\nabla^2f(\bar{x})$ is positive definite, then $\bar{x}$ is a strict local minimum of $f$ and moreover the linear perturbation of $f$, the function $f_v(x):=f(x)+v^Tx$ also has a strict local minimum point for each $v$ with sufficiently small norm. Moreover the condition $\nabla^2f(\bar{x})>0$ implies $f$ is locally convex around $\bar{x}$. This fact motivates us to the following question:

Suppose that $\bar{x}$ satisfies the following properties.

There exists $r>0$ such that:

• $\bar{x}$ is unique local minimum of $f$ on $\overline{B}(\bar{x},r)$;
• The linear perturbation function $f_v(x):=f(x)+v^Tx$ has a unique local minimum in $\overline{B}(\bar{x},r)$ for each $v$ with sufficiently small norm.

Here $\overline{B}(\bar{x},r)$ is the closed ball with center $\bar{x}$ and radius $r$.

Could we conclude that $f$ is locally convex around $\bar{x}$.

Thank you for all answers, constructive comments and useful references.

My question is related to the following topics:

1. Is a smooth function convex near a local minimum?
2. Local minimum implies local convexity?
3. Does a unique global and local minimum imply (strict) convexity?

Answer 1

Your conjecture is true. In fact it holds for all $C^1$ functions.

---

Before proving your conjecture, let me clarify what I mean by convexification of a function.

Notation:

• $B_t\subset \Bbb R^n, t>0$ is the open ball about $0$ with radius $t$;
• Consider a function $g:D \to \Bbb R$, where $D\subset \Bbb R^n$ is a convex set. The convexification $\mathop{co}(g)$ of $f$ is defined as $$ \mathop{co}(g)(x) = \inf \big\{y\in \Bbb R: (x,y)\in \mathop{co}(\mathop{epi}(g)) \big\} \quad \forall x\in D, $$ where $\mathop{co}(\mathop{epi}(g))$ denotes the convex hull of the epigraph of $g$.

Naturally, $g$ is convex iff it equals to its convexification $\mathop{co}(g)$.

---

Proof of the conjecture. For contradiction, suppose that there is a $C^1$ function $f:\Bbb R^n \to \Bbb R$, that is not locally convex at $0$, but there exist $r>0$ and $\delta>0$ such that the following conditions hold:

1. The origin $0$ is the unique local of $f$ on $B_r$;
2. The linear perturbation $f_v(x) \equiv f(x) + v^T x$ has unique local minimum on $B_r$ for any $v\in B_\delta$.

From the Condition 1 it follows that $\nabla f(0)=0$. Since $f$ is $C^1$, $\nabla f(x)$ is continuous, and so it converges to 0 as $x\to 0$. Let $0<\varepsilon<r$ be such that $\nabla f(x)\in B_\delta$ for all $x\in B_\varepsilon$.

Since $f$ is not locally convex at $0$, it is not convex on any neighborhood of the origin, specifically $f|_{B_\varepsilon}\neq \mathop{co}(f|_{B_\varepsilon})$, where $f|_{B_\varepsilon}$ denotes the restriction of the function $f$ to $B_\varepsilon$. Pick any $x^*\in B_\varepsilon$ such that $f(x^*) \neq y^* := \mathop{co}(f|_{B_\varepsilon})(x^*)$. Consider the supporting hyperplane $H$ of $\mathop{epi}(f|_{B_\varepsilon})$ at the point $(x^*,y^*)$, and write it as $$ H = \big\{ (x,y)\in \Bbb R^{n+1}: y + v^T x = y^* + v^T x^* \big\} $$ for some $v\in \Bbb R^n$. Since $f(x^*)\neq y^*$, the supporting hyperplane must touch the graph of $f$ at multiple points on $B_\varepsilon$. Let $x_0$ be any of those points. The hyperplane $H$ has to be tangent to the graph of $f$ at this point, thus $v=\nabla{f}(x_0)\in B_\delta$. However, this is a contradiction with the Condition 2, as it follows that the perturbation $f_v$ has multiple local minima on $B_{r}$.

Answer 2

We have,

$f_v(x) = f(x) + v^Tx$

$\nabla f_v(x) = \nabla f(x) + v$

Since $f_v(x)$ has a unique local minimum, we have $\nabla f_v(x) = 0$ at the minimum point say $x = x^*$.

We have, $\nabla f(x) +v = 0$. Hence we have $v = - \nabla f(x)$. Let this minima be $x^*$ i.e., $v = \nabla f(x^*)$. For this minima $x^*$ to be unique for every $v$, $x \rightarrow \nabla f(x)$ must be injective. This is because one can pick an $x_1,x_2$ with $\nabla f(x_1) = \nabla f(x_2)$ and choose $v = -\nabla f(x_1)$ and the minima for $f_v(x)$ is now at both points $x_1,x_2$. A contradiction to the uniqueness of minima of $f_v(x)$. Counter example for this injectivity seem to have appeared in an answer in this post for $n>1$.

For $n = 1$, If $x \rightarrow \nabla f(x) = f'(x)$ to be injective we must have $f'(x)$ to be increasing or decreasing.

So $f(x)$ is either convex or concave. But by the existence of a local minimum we conclude $f(x)$ is convex.

Answer 3

I was thinking this has a chance in $\mathbb R$ but once you step in $\mathbb R^2$ there should be counterexamples. Let us have a look at the polynomial function: $f\colon (x,y)\in \mathbb R^2 \longmapsto x^4 + 12 x^2 y^2 + y^4 + (x+2y)^2$. You can factor it as $f(x,y) = (x^2+y^2)^2 + 10x^2y^2 + (x+2y)^2$, this establishes that $f(0,0) = 0$ is the unique minimum.

We should note that $f$ is not locally convex around $(0,0)$. For example you can check that, \begin{equation} \begin{bmatrix} 2 \\ -1 \end{bmatrix}^\top \nabla^2 f(t,t) \begin{bmatrix} 2 \\ -1 \end{bmatrix} = -12t^2 < 0, \end{equation} for all $t \neq 0$, no matter how small.

It seemed that there existed a unique minimum for a small enough linear perturbation, however upon closer inspection the gradient map is not injective. I have plotted (rotated and resized) $\nabla f(r\cos \theta, r\sin\theta)$ with $r$ fixed smaller and smaller, and with $\theta$ varying from $0$ to $2 \pi$. It seems to describe a deformed circle around $(0,0)$ (it actually becomes close to a segment) but those circles actually overlap (see the attached plot). In any case the equation is, \begin{equation} \begin{bmatrix} 4 x^3 + 24 x y^2 + 2 (x + 2 y) \\ 24 x^2 y + 4 y^3 + 4 (x + 2 y) \end{bmatrix} = \begin{bmatrix} -u \\ -v \end{bmatrix}. \end{equation}

Arcs of the gradient are drawn, $\nabla f(r \cos t, r \sin t)$, for $r=10^{-7}(1+n/4)$ with $n=1,\dots,10$ and $t = 0 \dots 2\pi$. The picture has been rotated and stretched to show clearly the overlap.

Answer 4

BUGGY proof of $n=1$ special case There is a bug in the proof, which I am trying to fix when I have more time...

Disclaimer: I am not an expert (by a long shot), so you're most welcome to point out errors, loopholes, clarifications, etc. Thanks!

First, some simple "pre-processing" of the antecedents:

• For clarity I will write $B(l) = B(\bar{x}, l) = [\bar{x} - l, \bar{x} + l]$, i.e. the center of the neighborhood will always (implicitly) be $\bar{x}$.

• Assume $f$ is differentiable. Since $\bar{x}$ is a local minimum, $f'(\bar{x}) = 0$.

• Let $\epsilon > 0$ denote the upperbound for a "sufficiently small norm". I.e. $\forall v \in (-\epsilon, \epsilon)$ (equivalently, $|v| < \epsilon$): $f_v(x) = f(x) + vx$ has a unique local minimum in $B(r)$.

Lemma 1: there exists a neighborhood $B(a) = [\bar{x} - a, \bar{x} + a]$ for some $a > 0$ s.t. $\forall x \in B(a), | { f(x) - f(\bar{x}) \over x - \bar{x}} | < \epsilon$. Note that ${ f(x) - f(\bar{x}) \over x - \bar{x}}$ is the slope from $(x, f(x))$ to $(\bar{x}, f(\bar{x}))$. So this claim says there is a neighborhood where the absolute slope (from $\bar{x}$ to any other point) is bounded below $\epsilon$.

Proof of Lemma 1: (I think) this follows directly from the definition of derivative $f'(\bar{x}) = \lim_{x \rightarrow \bar{x}} { f(x) - f(\bar{x}) \over x - \bar{x}}$. Specifically, for any positive constant (here we choose $\epsilon$) there must be a neighborhood $B(a)$ s.t. the fraction ${ f(x) - f(\bar{x}) \over x - \bar{x}}$ stays entirely within $(f'(\bar{x}) -\epsilon, f'(\bar{x}) + \epsilon)$, which equals $(-\epsilon, \epsilon)$ because $f'(\bar{x}) = 0$. $\square$

At this point, we are dealing with two neighborhoods. The given $B(r)$ where the "unique local minimum" conditions apply, and the new $B(a)$ where the absolute slopes $< \epsilon$. Let $b = \min(r, a)$, s.t. $B(b)$ is the smaller of the two neighborhoods $B(r)$ and $B(a)$.

Main Result: $f$ is locally convex in $B(b)$.

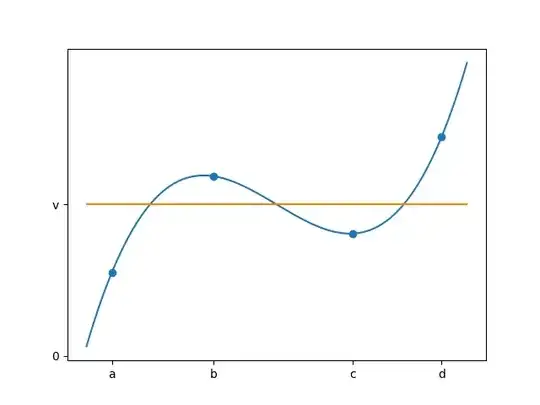
Main Proof: Assume for later contradiction that $f$ is not locally convex in $B(b)$. This means $\exists c, d$ s.t. $\bar{x} - b \le c < \bar{x} < d \le \bar{x} + b$ and the line segment $L$ connecting $(c, f(c))$ and $(d, f(d))$ does not lie entirely above $f$. [Bug alert: it is not OK to assume $c,d$ lie on different sides of $\bar{x}$.] Let the equation of the line segment $L$ be $L(x) = mx + q$ where $m$ is the slope and $q$ the intercept.

Lemma 2: $|m| = | {f(d) - f(c) \over d - c} | < \epsilon$.

Proof of Lemma 2: Since $\bar{x}$ is a unique local minimum in $B(r)$, it is also a unique local minimum in $B(b)$. Without loss, assume $f(d) > f(c)$. Then:

• $|f(d) - f(c)| < |f(d) - f(\bar{x})|$ since $f(d) > f(c) > f(\bar{x})$, and,

• $|d - c| > |d - \bar{x}|$ since $ d > \bar{x} > c$,

• therefore: ${ |f(d) - f(c)| \over |d - c| } < { |f(d) - f(\bar{x})| \over |d - \bar{x}| } < \epsilon$ since $d \in B(b) \subset B(a)$.

For the case of $f(c) > f(d)$, simply swap $c$ and $d$ in all 3 bullets above. $\square$

Continuing the main proof, we apply the perturbation antecedent condition with $v = -m$. Note that Lemma 2 proves that $|v| = |m| < \epsilon$, i.e. this chosen $v$ is of sufficiently small norm. Therefore, $f_v(x) = f(x) - mx$ has a unique local minimum in $B(r)$, which means it has 0 or 1 local minimum in $B(b) \subset B(r)$.

Recall that $L(x)$ does not lie entirely above $f(x)$ in the interval $[c,d]$, i.e. $\exists e \in (c,d)$ s.t. $f(e) > L(e)$. Consider $g(x) = f(x) - L(x)$. We have $g(c) = g(d) = 0$ and $g(e) > 0$. Since $f, L$ are continuous, so is $g$. Now, by the extreme value theorem:

• $g$ has a minimum in $[c,e]$, and since $g(e) > g(c)$, the minimum is actually in $[c,e)$.

• Similarly, $g$ has a minimum in $(e,d]$.

Therefore, $g$ has two minima in $[c,d]$. Since $f_v$ and $g$ only differ by a constant $q$, this means $f_v$ also has two minima in $[c,d] \subset B(b) \subset B(r)$. This is the desired contradiction.

Author's note: Again, I am no expert, so suggestions, comments, corrections most welcome!

Answer 5

Here is a proof for $n=1$. Let $f:\mathbb{R}\to\mathbb{R}$ be in $C^2$, and assume (without loss of generality) that $\bar{x}=0$ is a unique local minimum of $f$ in $B_r :=\{x\in\mathbb{R}:|x|<r\}$ and that $f(0)=0$. Assume furthermore that there exists $\epsilon>0$ such that any $f_v(x):=f(x) + v\cdot x$ has a unique local minimum in $B_r$ for all $|v|<\epsilon$.

We will show that the first derivative $h:=f'$ is non-decreasing in some neighborhood of $0$, which implies that $f$ is convex in that neighborhood, the desired result. The proof is by contradiction: we show that if $h$ is NOT non-decreasing near $0$, then it must contain infinitely many dog-leg turns converging on $0$. This contradicts the condition that $f_v$ has a unique solution near $0$ for small $v$.

First we prove that $h$ is non-decreasing on some small interval $[0,s]$. If $h$ is identically zero in a neighborhood of $0$, then $f\equiv 0$ in this neighborhood and is convex. So we may assume that $h$ is not identically zero near $0$. Note that $h$ cannot be uniformly $\leq 0$ in any interval $[0,s]$ since $0$ is a unique local minimum of $f$ in $[0,r]$ and $h$ is continuous. Thus, we may choose $d>0$ for which $h(d)>0$.

Assume to the contrary that $h$ is NOT non-decreasing in any interval $[0,s]$ for $s<r$. Then for any $0<\delta<h(d)$ there exists $v<\delta$ and $b<c<d$ with $0<h(b)<h(d)$ and $h(c)<v<h(b)$. This follows from the previous paragraph, the assumption about $h$ together with its continuity, and the fact that $h(0)=0$. For the same reason we may also choose $a<b$ with $h(a)<v$. Thus we have shown the existence of $0<a<b<c<d$ for which $h(a)<v<h(b)$ and $h(c)<v<h(d)$. The graph of $h$ in $[a,d]$ is depicted below.

It follows we may choose $\epsilon>0$ for which $I:=[v-\epsilon, v+\epsilon]$ is contained in $[h(a),h(b)]\cap [h(c),h(d)]$. Define the sets

$$P:=h(\{x\in[a,b]:h'(x)>0\})$$ $$P':=h(\{x\in[c,d]:h'(x)>0\})$$

Lemma $(I\cap P)\cap(I\cap P')$ is non-empty.
(Proof forthcoming. It proceeds by showing that $|I\cap P| = |I|$ where $|\cdot|$ is Lebesgue measure.)

The Lemma implies that there exists $y\in(I\cap P)\cap(I\cap P')$. Thus there exist $x_1\in[a,b]$ and $x_2\in[c,d]$ for which $h(x_1)=h(x_2)=y$ and $h'(x_1)>0, h'(x_2)>0$.

Since $f_v'(x) = h(x) + v$, we have shown that for any $s$ and sufficiently small $v$ there exists $x_1 \neq x_2$ for which $f_v'(x_j)=0$ and $f_v''(x_j)>0$. This contradicts the requirement that $f_v$ has a unique local minimum in $B_r$ for sufficiently small $v$.

Thus, $h$ is non-decreasing in $[0,s]$. A similar argument shows that $h$ is non-decreasing in $[t,0]$ for some $t<0$. It follows that $f$ is convex in $[t,s]$.