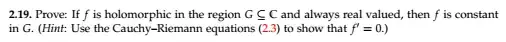I have questions on Part II of the same exercise asked here: $f(z)=u(x,y)+iv(x,y), u$ and $v$ are differentiable. Is $f$ differentiable?
$\label{1}{1}$. Is this ambiguous, but probably meant to say something like
if $u$ and $v$ are $\mathbb R^2-$ differentiable at a point $\mathbb R^2 \ni (x,y)$, then f is $\mathbb C-$ differentiable at the corresponding point point $\mathbb C \ni z=x+iy $
?
I hadn't considered $\mathbb R-$ vs $\mathbb C-$ differentiable.
$\label{2}{2}$. Is $f$ $\mathbb C-$differentiable if $u$ and $v$ are if $u$ and $v$ are $\mathbb C-$differentiable?
I think yes. Here is my reasoning. What are the errors, if any?
$$f'(z) := \lim_{h \to 0}\frac{f(z+h)-f(z)}{h} = \lim_{h \to 0}\frac{u(z+h)+iv(z+h)-u(z)-iv(z)}{h}$$
$$ = \lim_{h \to 0}\frac{u(z+h)-u(z)}{h} + i\lim_{h \to 0}\frac{v(z+h)-v(z)}{h} = u'(z)+iv'(z)$$
$\therefore, f$ is $\mathbb C$-differentiable at $z_0$ if $u$ and $v$ are complex differentiable. Furthermore, the $\mathbb C$-differentiability of $f$ is concluded by Definition (see end) and not by Cauchy-Riemann Thm 2.13(b) (see end). QED
$\label{3}{3}$. If $u$ and $v$ are complex differentiable, then do we have $f'(z)=u'(z)=v'(z)=0$ ?
I think yes. Here is my reasoning. What are the errors, if any?
I also hadn't considered that $u$ and $v$ are actually $\mathbb R$-valued. I cannot apply Exer 2.19 (see below), but by similar reasoning, I deduce that with Cauchy-Riemann Thm 2.13(a) and by the complex differentiability of $u$ at $z$, $u'(z)=0$. Similarly, $v'(z)=0$. $\therefore, f'(z)=0+i0=0.$ QED
$\label{4}{4}$. Is $f$ $\mathbb R^2-$differentiable if $u$ and $v$ are $\mathbb R^2-$differentiable?
It seems yes based on other question, but how would you prove it? Here is my reasoning. What are the errors, if any?
4.1. This book doesn't seem to have an explicit definition of $\mathbb R^2-$differentiability of a $\mathbb C$-function based on my other question, but I guess it's to do with treating $f=f(x,y)$ and $i$ as if $i$ were a $\mathbb R$-constant.
4.2. I thought to go back to the $\mathbb R^2-$differentiability in Stewart Calculus 14.4.7, but if $i$ is indeed treated as a $\mathbb R$-constant, then $f$ is a linear combination of $\mathbb R^2-$differentiable functions and $\therefore$ $\mathbb R^2-$differentiable.
Note: 4.1 is about definition. 4.2. is about the argument assuming my definition is the same as the book's reasonably deduced implicit definition, the book's explicit definition that I overlooked or some widely accepted definition of $R^2-$differentiability of a $\mathbb C$-function.
$\label{5}{5}$. Actually, $f$ is $\mathbb R^2-$differentiable only if $u$ and $v$ are $\mathbb R^2$-differentiable, by similar reasoning as in 4 whence
f is $\mathbb R^2$-differentiable $\iff$ $\Re(f)$ and $\Im(f)$ are $\mathbb R^2$-differentiable
?
$\label{6}{6}$. Is $f$ not necessarily $\mathbb C-$differentiable if $u$ and $v$ are if $u$ and $v$ are $\mathbb R^2-$differentiable?
Okay, so the answer is yes, answered in the aforementioned question again linked here. Here is my reasoning. What are the errors, if any?
As in the aforementioned question, $f(z)=\overline{z}=x-iy$ is not $\mathbb C-$differentiable. Instead of proving this directly with Cauchy-Riemann Thm 2.13(b), I will prove by contradiction and by considering $f$'s components:
Argument 1: If we try to write its derivative as $f'(z)=u'(z)+iv'(z)$, we see $f'(z)$ dne because the two addends $u'(z)$ and $iv'(z)$ do not exist because $u(z)$ and $v(z)$, while $\mathbb R^2$-differentiable, are not $\mathbb C$ differentiable, this time deduced by Cauchy-Riemann Thm 2.13(b). QED
Argument 1 rephrased: If we try to write $\overline{z}$'s derivative as $(\overline{z})'=(\Re(\overline{z}))'+i(\Im(\overline{z}))'$, we see $(\overline{z})'$ dne because the two addends $(\Re(\overline{z}))'$ and $i(\Im(\overline{z}))'$ do not exist because $\Re(\overline{z})$ and $\Im(\overline{z})$, while $\mathbb R^2$-differentiable, are not $\mathbb C$ differentiable, this time deduced by Cauchy-Riemann Thm 2.13(b). QED
Argument 2: (Same as Argument 1 except the last phrase) If we try to write $\overline{z}$'s derivative as $(\overline{z})'=(\Re(\overline{z}))'+i(\Im(\overline{z}))'$, we see $(\overline{z})'$ dne because the two addends $(\Re(\overline{z}))'$ and $i(\Im(\overline{z}))'$ do not exist because $\Re(\overline{z})=\Re(z)$ and $\Im(\overline{z})=-\Im(z)$, while $\mathbb R^2$-differentiable, are not $\mathbb C$ differentiable, because they don't satisfy C-R...which is a vacuous truth because they do satisfy C-R. Instead, we can prove by definition: $$\lim_{h \to 0} \frac{\Re(z+h)-\Re(z)}{h} = \lim_{h \to 0} \frac{h_x}{h_x+ihy}$$
This does not exist because along $h_x=0$, $\lim=0$ while along $h_y=0$, $\lim=1$.
Similarly,
$$\lim_{h \to 0} \frac{-\Im(z+h)+\Im(z)}{h} = \lim_{h \to 0} \frac{-h_y}{h_x+ihy}$$
This does not exist because along $h_y=0$, $\lim=0$ while along $h_x=0$, $\lim=i$.
Argument 3: Same as argument 2 except that I say that the parts are not complex differentiable and hence $f$ is not complex differentiable, but I see why is this wrong as well.
$\label{7}{7}$. If Reasoning in 6 (Argument 1) is right, then we actually have additionally proved (hope none of those modifiers were misplaced!) that
f is $\mathbb C$-differentiable $\iff$ $\Re(f)$ and $\Im(f)$ are $\mathbb C$-differentiable
?
(Note: Vacuous truths acceptable! Hehe) --> i.e. Update: Reasoning in 6 was (Argument 1 is) wrong, conclusion is wrong, but conclusion is right if Argument 1 is right! Hehe
Definition of $\mathbb C$-differentiability
Cauchy-Riemann Thm 2.13(a)(b)
Exer 2.19