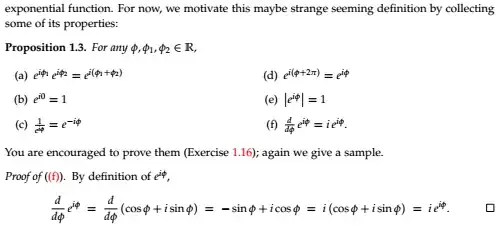Discussing $\frac{d}{d\theta}e^{i\theta}$ aka cis before complex derivatives and complex exponential

Question

A First Course in Complex Analysis by Matthias Beck, Gerald Marchesi, Dennis Pixton, and Lucas Sabalka

Definition of $e^{i \theta}$ (or cis in other texts)

About Prop 1.3f, how is it possible to discuss derivative of $e^{i \theta}$ before both defining derivatives of complex functions (Ch2) (including functions of a real variable I think!) and defining the complex exponential (Ch3)?

In particular, the proof of Prop 1.3f seems to assume linearity of the derivatives of complex functions.

There's even this exercise later on: Exer 1.6b

I know how to do this with Ch3's definition of the complex exponential. I don't believe this is possible to do with only Ch1 even if we write $e^{\phi + i\phi} = e^{(i+1)\phi}$.

Your link does not work, it's behind a firewall, most likely. — Lee Mosher, Jul 29 '18 at 13:28
For your Q1, this is the derivative of a complex valued function of a real variable. So you do not need complex derivatives. — Kusma, Jul 29 '18 at 13:30
I'm closing this as too broad as there are too many questions. — Shaun, Jul 29 '18 at 13:30
@Shaun Ok thanks. I took off De Moivre and made the question on derivatives only. — BCLC, Jul 29 '18 at 13:34
@Kusma But still, how do we know complex constants can be treated the way real constants are? Oh wait, is it possible some universities or textbooks teach (or assume students were taught) derivatives of $f: \mathbb R \to \mathbb C$ ? I'm thinking perhaps the textbook assumes students know $$\frac{d}{dx} cf(x) = c\frac{d}{dx} f(x) \ \forall c \in \mathbb C$$? — BCLC, Jul 29 '18 at 13:35
There's still one too many questions. Keep it to one at a time, please. — Shaun, Jul 29 '18 at 13:35
I deleted my other comment because I though the comment of @Kusma was a much better explanation. — Lee Mosher, Jul 29 '18 at 15:33

Ross Millikan · Answer 1 · 2018-07-29T16:43:44.287

3

As the author states, this is just a definition of a function of $\phi$ and could have been denoted $q(\phi)$. This notation is chosen because it will accord with our definition of real and complex exponentiation. It can be hard to look at $e^{i\phi}$ and remember (until chapter 3) that you don't know this is the complex exponential, you just know it is this function of $\phi$.

The properties in $1.3$ can all be verified directly from the definition and the usual trig identities. In particular for $1.3f$ we have $$\frac d{d\phi}e^{i\phi}=\frac d{d\phi}(\cos \phi +i\sin \phi)=-\sin \phi+i\cos \phi=ie^{i\phi}$$ Note that the rule for differentiating an exponential was not used.

The challenge I see for $1.6b$ comes from mixing the real and imaginary numbers in the exponential. Even if you have already defined the exponential function for real arguments, we need to define $e^{a+bi}=e^ae^{bi}$ and I don't see a definition of that unless you have defined the sine and cosine of imaginary numbers. If you are given that definition and have the derivative of the real exponential you can prove what is desired.

edited Jul 29 '18 at 16:43

answered Jul 29 '18 at 13:55

Ross Millikan

374,822

Ross Millikan, thanks. I know what cis(theta) is. I had to take out because of Shaun. Anyhoo, for 1.3f, why can you take out i in the derivative? Sure you can take out REAL constants but DOES THIS APPLY TO COMPLEX CONSTANTS? Of course yeah in Ch2, but this is still Ch1. What's the justification for treating complex constants the way we would real ones? For exer 1.6b, you agree that it cannot be done with Ch1 only? – BCLC Jul 29 '18 at 16:08
1

The first equality in my 1.3f is just the definition. Then for the second you need to take off the multiplicative $i$ and apply the usual rule for the trig functions. I don't know what you have covered at this point. I would have thought you would have $(ax)'=ax'$ for constant $a$ even if it is complex. If you don't then the middle inequality is not justified. That is one of the hazards of defining such a suggestive notation. You tend to forget what you are not allowed to do with it. – Ross Millikan Jul 29 '18 at 16:13
1

@rossmillikan Hi Ross. If I understand the main concern of the OP, it is that the author has yet to prove that $$\frac{d}{d\phi}\left(\cos(\phi)+i\sin(\phi)\right)=\frac{d\cos(\phi)}{d\phi}+\frac{d i\sin(\phi)}{d\phi}$$and then ALSO that $$\frac{d i\sin(\phi)}{d\phi}=i\frac{d \sin(\phi)}{d\phi}$$That is, no rules for differentiating complex-valued functions of a real variable have been established. – Mark Viola Jul 29 '18 at 16:14
@MarkViola that's right and thanks! Although Ross Millikan posted a comment about a minute before you did in case you didn't see. – BCLC Jul 29 '18 at 16:22
1

@BCLC Ross didn't mention the first equality in my comment. – Mark Viola Jul 29 '18 at 16:27
1

Indeed you need to establish the identities @MarkViola mentioned, but that is easy to do once you know what convergence means for sequences / functions involving complex numbers. – Kusma Jul 29 '18 at 16:27
@MarkViola right thanks. I meant to ask about that too but sleepy and using phone. – BCLC Jul 29 '18 at 16:29
@Kusma ONCE YOU KNOW. But when you're in Ch1, how to do?!?!? Convergence isn't even until Ch7 soooo.... (I already finished the book and am now revising, so I kinda know what you're getting at for the post-Ch1 approach/es) – BCLC Jul 29 '18 at 16:31
@RossMillikan wait the 'you' in 'you tend' refers to the authors? – BCLC Jul 29 '18 at 16:33
1

Yes, I meant the authors can get sloppy about what has been justified and what not. Please do not edit comments into the answer. – Ross Millikan Jul 29 '18 at 16:44
1

Alternatively you can just define the real derivative of a complex valued function as derivative of real part plus i times derivative of imaginary part. Then you can easily differentiate $e^{i\phi}$. – Kusma Jul 29 '18 at 16:50
@Kusma I was thinking that. Kind of like integrals at the beginning of Ch4. Thanks! But that solves prop1.3f and not exer1.6b? – BCLC Jul 30 '18 at 00:32
@MarkViola post an answer? It seems other answerer disagrees with you/us/me – BCLC Jul 30 '18 at 01:52

score 0 · Answer 2 · answered Jul 29 '18 at 16:51

0

When we define $e^{i\phi} = \cos \phi +i\sin \phi$ the only information from complex numbers is that $i$ is a constant whose square is $-1$

You can use the algebra of the complex field without using differentiation theorems of complex variables.

When we prove $\frac {d}{dz}z^2=2z$ using the definition of derivative we are using complex variables, but when we use $\frac {d}{d\phi }(cos \phi + i\sin \phi)= -\sin \phi + i \cos \phi $ we are just using differentiation rules of real vlued functions, $\sin x$ and $\cos x$ with the algebra of complex numbers.

answered Jul 29 '18 at 16:51

Mohammad Riazi-Kermani

68,728

Do you disagree with Mark Viola? Quote: the author has yet to prove that $$\frac{d}{d\phi}\left(\cos(\phi)+i\sin(\phi)\right)=\frac{d\cos(\phi)}{d\phi}+\frac{d i\sin(\phi)}{d\phi}$$and then ALSO that $$\frac{d i\sin(\phi)}{d\phi}=i\frac{d \sin(\phi)}{d\phi}$$That is, no rules for differentiating complex-valued functions of a real variable have been established. – BCLC Jul 30 '18 at 00:35
@BCLC Yes, I think there is no need for further rules to differentiate$$ \frac{d}{d\phi}\left(\cos(\phi)+i\sin(\phi)\right)=\frac{d\cos(\phi)}{d\phi}+\frac{id\sin(\phi)}{d\phi}$$ – Mohammad Riazi-Kermani Jul 30 '18 at 01:44
but how do we know that the imaginary number works the way all the real numbers do AT THIS POINT in the text? – BCLC Jul 30 '18 at 01:51
$i$ is a constant and we treat it like a constant. The rest is all real. – Mohammad Riazi-Kermani Jul 30 '18 at 01:54
sure that works for constants on the real line but what about constants elsewhere in the complex plane? :| – BCLC Jul 30 '18 at 02:47
Also what's your answer to Exer1.6b? – BCLC Jul 30 '18 at 02:48
@BCLC I think a more general definition for $e^{a+ib}$ instead of just $e^{ib}$would have been more appropriate. – Mohammad Riazi-Kermani Jul 30 '18 at 04:04
so you agree that Exer1.6b cannot be answered with Ch1 alone? – BCLC Jul 30 '18 at 04:11
I agree that a hint or a definition would have helped. – Mohammad Riazi-Kermani Jul 30 '18 at 04:17
@BCLC Thanks for your attention. – Mohammad Riazi-Kermani Jul 30 '18 at 04:30
What's your answer to 'sure that works for constants on the real line but what about constants elsewhere in the complex plane? :|' ? – BCLC Jul 30 '18 at 23:08

BCLC · Accepted Answer · 2021-09-21T15:11:41.120

I believe it's a mistake in the way that Mark Viola describes.

The correction to the mistake is I think as follows:

I suspect a definition (*) such as

$$\frac{d}{d\theta}x(\theta)+iy(\theta) := \frac{d}{d\theta}x(\theta)+i\frac{d}{d\theta}y(\theta) \tag{1}$$

instead of something like 'we can treat $i$ as constant.

I think $(1)$ can be viewed as natural if you consider $z(\theta):=x(\theta)+iy(\theta) \in \mathbb C$ as a vector $\in \mathbb R^2$ s.t.

$$z(\theta) = [x(\theta),y(\theta)] \in \mathbb R^2$$

Then

$$z'(\theta)= [x'(\theta),y'(\theta)]$$

(*) Definition is in Ch2.3. see the 2 red boxes below.

Discussing $\frac{d}{d\theta}e^{i\theta}$ aka cis before complex derivatives and complex exponential

3 Answers3

Linked