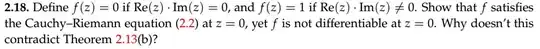How is $f(z)=1_{xy \ne 0}$ not complex differentiable? I know $f(x,y)=1_{xy \ne 0}$ isn't real-differentiable

Question

A First Course in Complex Analysis by Matthias Beck, Gerald Marchesi, Dennis Pixton, and Lucas Sabalka Exer 2.18

---

• This is for complex analysis, but I have a feeling this might be answered mostly Calculus III. Thm 2.13 is Cauchy-Riemann.

• Re title: On $\mathbb R^2-$ vs $\mathbb C-$ differentiability of $f, \Re(f)$ and $\Im(f)$

---

1. Is my understanding of the following solution right, and why/why not?

At a Winter 2017 course in Oregon State University, there's a solution given: It seems to be saying that $f$ is not continuous and therefore conditions of Cauchy-Riemann do not hold because of some relationship between the continuity of $f$ and then parts of $f_x$ and $f_y$ and somehow the assumptions of C-R are equivalent to continuous differentiability.

Note: I assume the 'Theorem 2.15(b)' refers to an old edition, w/c is not relevantly different from the current edition, in w/c Cauchy-Riemann is in Thm 2.13.

2. Here is my solution. Where have I gone wrong, if anywhere, and why?

Rewrite $f(z) = f(x,y) = 1_{xy \ne 0}(x,y)$ s.t.

$$f_x(0,0) := \lim_{\Delta x \to 0} \frac{1_{00+\Delta x 0 \ne 0} - 1_{00 \ne 0}}{\Delta x} = \lim_{\Delta x \to 0} \frac{0-0}{\Delta x} = \lim_{\Delta x \to 0} 0 = 0$$

Similarly, $f_y(0,0) = 0$.

$$\therefore, f_x(0,0) = 0 = -i0 = -if_y(0,0)$$

Now $f_x(0,0)$ may be defined, but $f_x$ neither is continuous at $0$ nor exists on any disc centred at $0$ because $f_x$ does not exist along $x_0=0$:

$$f_x(0,y_0) = \lim_{\Delta x \to 0} \frac{1_{0y_0+\Delta x y_0 \ne 0} - 1_{0y_0 \ne 0}}{\Delta x} = \lim_{\Delta x \to 0} \frac{1_{\Delta x y_0 \ne 0}-0}{\Delta x} = \lim_{\Delta x \to 0} \frac{1}{\Delta x} \ \text{, w/c dne.}$$

Similar holds for $f_y$ along $y_0 =0$.

$\therefore,$ Cauchy-Riemann holds at $z=0$ but $f$ is not differentiable at $z=0$ because $f_x$ is not continuous at $z=0$ because $f_x$ does not exist along $x_0=0$.

Answer 1

That a function $f$ is complex differentiable at a point $z_0$ means that the derivative $$ f'(z_0) = \lim_{\mathbb{C} \ni h \to 0} \frac{f(z+h)-f(z)}{h} $$ exists.

Now, if $f$ (i.e. the real and imaginary parts of $f$) is real differentiable, and Cauchy-Riemann's equations are satisfied at $z_0$, this implies that $f$ is complex differentiable at $z_0$.

Note also, that existence of partial derivatives is not enough to conclude real differentiability!

Answer 2

Recall that being complex differentiable means the Cauchy--Riemann equations holds and that the function is real differentiable at that point. This function is not real differentiable at the origin.

With respect to the second comment: if the partial derivatives exist in a neighborhood of the point and are continuous, then the function is real differentiable, so this plus Cauchy--Riemann gives complex differentiablity, in light of the previous paragraph.