Fourier transform of $\frac{\sin{x}}{x}$

Question

can you help me with this question find $\sin$ Fourier transform of $\frac{\sin{x}}{x}$

Answer 1

I write the Fourier transform as

$$\hat{f}(v) = \int_{-\infty}^{\infty} dx \: \frac{\sin{x}}{x} e^{-i 2 \pi v x} $$

Consider, rather, the integral

$$ \frac{1}{i 2} \int_{-\infty}^{\infty} dx \: \frac{e^{i x}-e^{-i x}}{x} e^{-i 2 \pi v x} $$

$$ = \frac{1}{i 2} \int_{-\infty}^{\infty} dx \: \frac{e^{i (1-2 \pi v) x}}{x} - \frac{1}{i 2} \int_{-\infty}^{\infty} dx \: \frac{e^{-i (1+2 \pi v) x}}{x} $$

Consider the following integral corresponding to the first integral:

$$\oint_C dz \: \frac{e^{i (1-2 \pi v) z}}{z} $$

where $C$ is the contour defined in the illustration below:

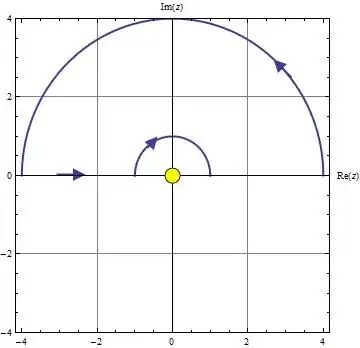
This integral is zero because there are no poles contained within the contour. Write the integral over the various pieces of the contour:

$$\int_{C_R} dz \: \frac{e^{i (1- 2 \pi v)z}}{z} + \int_{C_r} dz \: \frac{e^{i (1- 2 \pi v) z}}{z} + \int_{-R}^{-r} dx \: \frac{e^{i (1- 2 \pi v) x}}{x} + \int_{r}^{R} dx \: \frac{e^{i (1- 2 \pi v) x}}{x} $$

Consider the first part of this integral about $C_R$, the large semicircle of radius $R$:

$$\int_{C_R} dz \: \frac{e^{i (1- 2 \pi v)z}}{z} = i \int_0^{\pi} d \theta e^{i (1-2 \pi v) R (\cos{\theta} + i \sin{\theta})} $$

$$ = i \int_0^{\pi} d \theta e^{i (1-2 \pi v) R \cos{\theta}} e^{-(1- 2 \pi v) R \sin{\theta}} $$

By Jordan's lemma, this integral vanishes as $R \rightarrow \infty$ when $1-2 \pi v > 0$. On the other hand,

$$ \int_{C_r} dz \: \frac{e^{i (1-2 \pi v) z}}{z} = i \int_{\pi}^0 d \phi \: e^{i (1-2 \pi v) r e^{i \phi}} $$

This integral takes the value $-i \pi$ as $r \rightarrow 0$. We may then say that

$$\begin{align} & \int_{-\infty}^{\infty} dx \: \frac{e^{i (1-2 \pi v) x}}{x} = i \pi & 1-2 \pi v > 0\\ \end{align}$$

When $1-2 \pi v < 0$, Jordan's lemma does not apply, and we need to use another contour. A contour for which Jordan's lemma does apply is one flipped about the $\Re{z}=x$ axis. By using similar steps as above, it is straightforward to show that

$$\begin{align} & \int_{-\infty}^{\infty} dx \: \frac{e^{i (1-2 \pi v) x}}{x} = -i \pi & 1-2 \pi v < 0\\ \end{align}$$

Using a similar analysis as above, we find that

$$\int_{-\infty}^{\infty} dx \: \frac{e^{-i (1+2 \pi v) x}}{x} = \begin{cases} -i \pi & 1+2 \pi v < 0 \\ i \pi & 1+2 \pi v >0 \\ \end{cases} $$

We may now say that

$$\hat{f}(v) = \int_{-\infty}^{\infty} dx \: \frac{\sin{x}}{x} e^{-i 2 \pi v x} = \begin{cases} \pi & |v| < \frac{1}{2 \pi} \\ 0 & |v| > \frac{1}{2 \pi} \\ \end{cases} $$

Answer 2

Note that the sinc function is not in $L^1$; therefore you cannot compute its Fourier transform in the "obvious" way by means of the residue theorem or something like that. But this function is in $L^2$, so it is indeed Fourier related to some other function $f\in L^2$. If we can guess an $f$ such that its inverse Fourier transform is sinc we are done.

Now we know from Fourier series as well as from Fourier transform that sinc turns up when processing a rectangle pulse. Therefore we try $$f(\omega):=\cases{c\quad &$\bigl(|\omega|< \Omega\bigr)$ \cr 0&$\bigl(|\omega|> \Omega\bigr)$ \cr}$$ with parameters $c$ and $\Omega$ yet to be determined. At any rate $${\cal F}^{-1}f(x)=\int_{-\infty}^\infty f(\omega)e^{i\omega x}\ d\omega=c\int_{-\Omega}^\Omega e^{i\omega x}\ d\omega={2c\sin(\Omega x)\over\Omega}\ .$$ Now adjust the parameters $c$ and $\Omega$ to your needs. (Note that your definition of ${\cal F}$, resp. ${\cal F}^{-1}$, might lead to slightly different values.)

Answer 3

You've got:

$$F(w) = \int \frac{\sin x}{ x} exp(-iw x) dx$$

Differentiate wrt $w$ to get:

$$F'(w) = -i \int \sin x exp(- iwx)dx $$

You know how to find fourier transform of sine and then you should integrate your result.

Answer 4

Here is another perspective on the problem: Using $\sin(x) = \frac{1}{2i}(e^{ix}-e^{-ix})$ one easily calculates $$ \mathcal{F} \sin = \frac{1}{2} i \left( \delta_{-\frac{1}{2\pi}} - \delta_{\frac{1}{2\pi}} \right), \tag{1} $$ where $\delta_x$ is the Dirac distribution concentrated at $x$. Now, we use that - intuitively speaking - the Fourier transform changes differentiation into multiplication with $x$. More precisely, we have (using the notation $\chi: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto x$) $$ \left( \mathcal{F} \, \frac{\sin(\chi)}{\chi} \right)' = \mathcal{F} (-2 \pi i \chi) \frac{\sin(\chi)}{\chi} = (-2 \pi i) \mathcal{F} \sin $$ and substituting (1) yields $$ \left( \mathcal{F} \, \frac{\sin(\chi)}{\chi} \right)' = \pi \left( \delta_{-\frac{1}{2\pi}} - \delta_{\frac{1}{2\pi}} \right). $$ This tells us that $\mathcal{F} \, \frac{\sin(\chi)}{\chi}$ makes an upward jump of height $\pi$ at $-\frac{1}{2\pi}$ and a downward jump of height $\pi$ at $\frac{1}{2\pi}$. From that one obtains $$ \mathcal{F} \, \frac{\sin(\chi)}{\chi} = \pi 1_{(-\frac{1}{2\pi}, \frac{1}{2\pi})} + C $$ for some constant $C$, where $1_A$ denotes the characteristic function of $A$. Finally, it is no problem to check that $C$ must be $0$.