The basis of this problem, and that which allows for the approximations to be made here, can be summarised in one approximation:
$$\Biggl(\frac{n^k -{\lfloor n^{\frac{1}{k}} \rfloor}^{k-1}\gcd({\lfloor n^{\frac{1}{k}} \rfloor}^{k-1},\Bigl\lfloor \frac{p_n^{k-1}}{n^{k-1}} \Bigr\rfloor)}{n^k -{\lfloor n^{\frac{1}{k}} \rfloor}\gcd({\lfloor n^{\frac{1}{k}} \rfloor},\Bigl\lfloor \frac{p_n^{k}}{n^{k}} \Bigr\rfloor)}\Biggr)^{\frac{1}{k}} \approx 1\quad\forall n,k \in \mathbb N\backslash {\{1}\}$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(A0)$$
$$\frac{\Bigl\lfloor \bigl(n^k -{\lfloor n^{\frac{1}{k}} \rfloor}^{k-1}\gcd({\lfloor n^{\frac{1}{k}} \rfloor}^{k-1},\Bigl\lfloor \frac{p_n^{k-1}}{n^{k-1}} \Bigr\rfloor)\bigr)^{\frac{1}{k}}\Bigr\rfloor }{\Bigl\lfloor \bigl(n^k -{\lfloor n^{\frac{1}{k}} \rfloor}\gcd({\lfloor n^{\frac{1}{k}} \rfloor},\Bigl\lfloor \frac{p_n^{k}}{n^{k}} \Bigr\rfloor)\bigr)^{\frac{1}{k}}\Bigr\rfloor} =1\quad\forall n,k \in \mathbb N\backslash {\{1}\}$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(A1)$$
$${\gcd\Bigl({\lfloor n^{\frac{1}{k}} \rfloor},\Bigl\lfloor \frac{p_n^k}{n^k} \Bigr\rfloor\Bigr)}\quad \Biggl|\quad \lfloor n^{\frac{1}{k}} \rfloor \gcd\Bigl({\lfloor n^{\frac{1}{k}} \rfloor}^{k-1},\Bigl\lfloor \frac{p_n^{k-1}}{n^{k-1}} \Bigr\rfloor\Bigr) $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(A2)$$
Defining the above ratio as varsigma: $$\varsigma_{n,k}= \frac{{{\lfloor n^{\frac{1}{k}} \rfloor}^{k-1}\gcd\Bigl({\lfloor n^{\frac{1}{k}} \rfloor}^{k-1},\Bigl\lfloor \frac{p_n^{k-1}}{n^{k-1}} \Bigr\rfloor\Bigr)} }{{\gcd\Bigl({\lfloor n^{\frac{1}{k}} \rfloor},\Bigl\lfloor \frac{p_n^k}{n^k} \Bigr\rfloor\Bigr)}}$$
We have the following:
$n \lt 2^k \Rightarrow \varsigma_{n,k}=1$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(A3)$$
The maximum value of the integer remainder of the division of $n^k+m$ by $\gcd(\Bigl\lfloor \frac{p_n^{\, a}}{n^{\,b}} \Bigr\rfloor,n^c)$ is equal to $m$, when $a \gt 1$, $b \gt 1$ and $1 \leq c \leq k$.
This stated in inequalities:
$$a \gt 1\land b \gt 1 \land 1 \leq c \leq k \Rightarrow -m \leq n^k-\Biggl\lfloor\frac{n^k+m}{\gcd(\Bigl\lfloor \frac{p_n^{\, a}}{n^{\,b}} \Bigr\rfloor,n^c)}\Biggr\rfloor\gcd\Biggl(\Bigl\lfloor \frac{p_n^{\, a}}{n^{\,b}} \Bigr\rfloor,n^c\Biggr) \leq 0$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(A7)$$
So the question I am now asking, for that fun person that wants to close this page, is how do I establish a proof for (A5) and (A7) that will be rigorous and indisputable?
note that for now, I will leave the lemma as the restriction
$${\{a,b}\} \subset \mathbb N \land c \in {\{1,2,3,...,k}\} \Rightarrow n^k+m-\Biggl\lfloor\frac{n^k+m}{\gcd(\Bigl\lfloor \frac{p_n^{\, a}}{n^{\,b}} \Bigr\rfloor,n^c)}\Biggr\rfloor\gcd\Biggl(\Bigl\lfloor \frac{p_n^{\, a}}{n^{\,b}} \Bigr\rfloor,n^c\Biggr) \in {\{0,1,2,...,m}\}$$
But there most definitely exists congruence relations that have dependence in $(n,k)$ that allow us to reduce this condition to a specific subset of the least residue system modulo $m+1$ stated on the righthand side of the implicative arrow.
ADDITION NEEDED:
I apologize a lot if making another edit here again cause the website to spiral into chaotic unrest somehow, but the following lemma pertaining to the residues of the floor function of natural numbers raised to unit fraction exponents (as we see playing one of the most significant role in the original formula I found and stated in this discussion page), is very significant to the context as previously stated:
$$y \in{\{j \in \mathbb N : j=k^m+1 \land m \in\mathbb N\backslash {\{1}\} \land k \in\mathbb N }\}\Rightarrow \not\exists\, n \in \mathbb N \backslash {\{1}\}:\lfloor y^{\frac{1}{m}}\rfloor^{m}\equiv y (\operatorname{mod}n)$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(\operatorname{Residue000})$$
Attempting to simplify the above:
$$\exists\,\\ m \in \mathbb N \backslash {\{1}\}\,\,: (y-1)^{\frac{1}{m}}\equiv 0 (\operatorname{mod}1)\Rightarrow \not\exists\, n \in \mathbb N \backslash {\{1}\}:\lfloor y^{\frac{1}{m}}\rfloor^{m}\equiv y (\operatorname{mod}n)$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(\operatorname{Residue001})$$
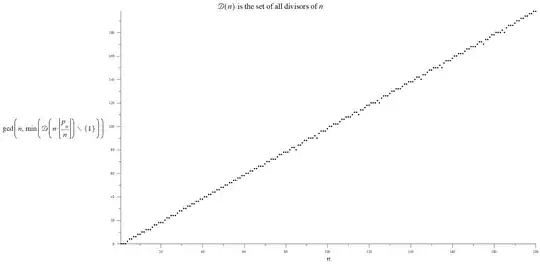
Yesterday I noticed quite a strong fit for the approximation: $$\vartheta _{{n}}=\min\Biggl(\mathcal D\Bigl(n\cdot\Bigl\lfloor \frac{p_n}{n} \Bigr\rfloor\Bigr) \backslash {\{1}\}\Biggr)$$ $$n-\gcd(\bigl\lfloor \sqrt {n} \bigr\rfloor ,\vartheta _{{n}})) \approx A \cdot (n-1) +B$$
where $A \approx 1$ and $B \approx -1/2$ and $\mathcal D(n)$ denote the set of all divisors of $n$, $p_n$ is the $n^{th}$ prime.
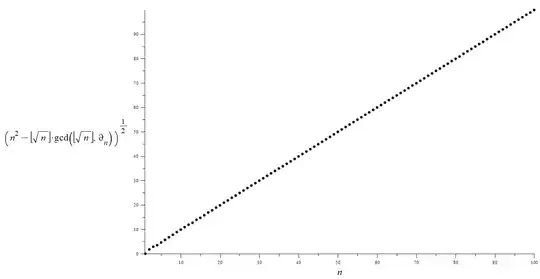
$$\sqrt{\bigl( n^{2}-\bigl\lfloor \sqrt {n} \bigr\rfloor\cdot\gcd(\bigl\lfloor \sqrt {n} \bigr\rfloor ,\vartheta _{{n}})\bigr)}\sim n $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R1)$$
$$\sqrt{\bigl( n-\gcd(n ,\vartheta _{{n}})\bigr)}+\frac{1}{\sqrt{n}}\sim \sqrt{n}$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R2)$$
$$\sqrt{{n}^{2}-\max \left( \lfloor \sqrt{n} \rfloor ,n \right) \min \left( \gcd \left( \lfloor \sqrt{n} \rfloor,\vartheta_n \right) ,\gcd \left( n,\vartheta_n \right) \right) }+1+\delta_{{n}}\sim n$$
Where $\delta_n \in {\{-\frac{1}{2},0,\frac{1}{2}}\}$ is a discrete function for which I am unable to determine as yet. $$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R3)$$
So I guess the best idea now would be for me to find either a value on $\mathbb N$ that satisfies neither of the following equalities: $$n- \Biggl(\Bigl\lfloor\sqrt {{n}^{2}- \lfloor \sqrt{n} \rfloor \cdot \gcd \left( \lfloor \sqrt{n} \rfloor ,\vartheta_n \right) } \Bigr\rfloor+1\Biggr) = 0 $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R4)$$
$$n-\Biggl(\Bigl\lfloor \sqrt{{n}^{2}-\min \left( \lfloor \sqrt{n} \rfloor ,n \right)\cdot\min\left(\gcd ( \lfloor \sqrt{n}\rfloor,\vartheta_n) ,\gcd ( n,\vartheta_n) \right) }\Bigr\rfloor +1\Biggr) = 0$$ $$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R5)$$
Figure 2:
Defining a generalisation of vartheta: $$\vartheta _{{n,k}}=\min\Biggl(\mathcal D\Bigl(n^{k}\cdot\Bigl\lfloor \frac{p_n^{k}}{n^{k}} \Bigr\rfloor\Bigr)\, \backslash\, {\{1}\}\Biggr)$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R6)$$
Will allow for the following asymptotic relation as we would intuitively expect from the nature of the generalisation and the nature of $(R2)$: $$(n^k -\lfloor n^{\frac{1}{k}} \rfloor\gcd(\lfloor n^{\frac{1}{k}} \rfloor,\vartheta _{{n,k-1}}))^{\frac{1}{k}} \sim n \quad \forall k \in \mathbb N\backslash {\{1}\}$$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R7)$$
Which is based on the following equalities:
$$\lfloor (n^k -\lfloor n^{\frac{1}{k}} \rfloor\gcd(\lfloor n^{\frac{1}{k}} \rfloor,\vartheta _{{n,k-1}}))^{\frac{1}{k}} \rfloor+1=n\quad \forall k \in \mathbb N\backslash {\{1}\} $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R8)$$
$$\lfloor (n^k -\gcd(\lfloor n^{\frac{1}{k}} \rfloor,\Bigl\lfloor \frac{p_n^{k}}{n^{k}} \Bigr\rfloor))^{\frac{1}{k}} \rfloor+1=n\quad \forall k \in \mathbb N\backslash {\{1}\} $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R9)$$
$$\lfloor (n^k -{\lfloor n^{\frac{1}{k}} \rfloor}^{k-1}\gcd({\lfloor n^{\frac{1}{k}} \rfloor}^{k-1},\Bigl\lfloor \frac{p_n^{k-1}}{n^{k-1}} \Bigr\rfloor))^{\frac{1}{k}} \rfloor+1=n\quad \forall k \in \mathbb N\backslash {\{1}\} $$
$$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(R10)$$