Like @dxiv, I considered the central angles. Unlike @dxiv, I reached a positive verdict:
Your pieces should fit.
We know your pieces are perfect right triangles that fit together in pairs as follows:
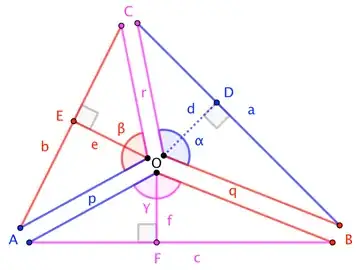
To determine whether they fit together in one whole, we need only determine whether $\alpha+\beta+\gamma = 360^\circ$. Well,
$$\begin{align}
\sin(\alpha+\beta+\gamma) &=
\sin\alpha\cos\beta\cos\gamma + \cos\alpha\sin\beta\cos\gamma
+\cos\alpha\cos\beta\sin\gamma - \sin\alpha\sin\beta\sin\gamma \\
\cos(\alpha+\beta+\gamma) &=
\cos\alpha\cos\beta\cos\gamma -
\cos\alpha\sin\beta\sin\gamma -
\sin\alpha\cos\beta\sin\gamma -
\sin\alpha\sin\beta\cos\gamma
\end{align}$$
where
$$\cos\alpha = \frac{-a^2+q^2+r^2}{2qr} \qquad
\cos\beta = \frac{-b^2+r^2+p^2}{2rp} \qquad
\cos\gamma = \frac{-c^2+p^2+q^2}{2pq}$$
$$\sin\alpha = \frac{2|\triangle OBC|}{qr} = \frac{ad}{qr} \qquad
\sin\beta = \frac{be}{rp} \qquad \sin\gamma = \frac{cf}{pq}$$
Substituting ...
$$a \to 493 + 2107 \qquad b \to 675 + 1925 \qquad c \to 1053 + 403$$
$$d \to 276 \qquad e \to 900 \qquad f \to 396$$
$$p \to 1125 \qquad q \to 565 \qquad r \to 2125$$
... Mathematica calculates (via precise integer arithmetic) ...
$$\sin(\alpha+\beta+\gamma) = 0 \;\;\text{(exactly)} \qquad\qquad \cos(\alpha+\beta+\gamma) = 1\;\;\text{(exactly)}$$
... so that (subject to the accuracy of your measurements) $\alpha+\beta+\gamma$ is definitely an integer multiple of $360^\circ$. By inspection, the integer multiplier is $1$. $\square$

