1

I have a triangle $(5,6,7)$, that is $a=5$, $b=6$, $c=7$ and I want to find the coordinates of the vertices on the $xy$ plane in a manner that I can implement in a program or a spreadsheet. I let $(x_{ac},y_{ac})=(0,0)$. I let $(x_{bc},y_{bc}=(7,0$). Then, from the law of cosines, to get $(x_{ab},y_{ab})$, I let

$$x_{ab}=a*\cos⁡(\alpha)=a*\frac{a^2+c^2-b^2}{2ab}=5*\frac{25+49-36}{2*5*7}=\frac{38}{14}=2.714285714285714$$ and this appears to be the correct value according to answers to my earlier question.

I can use this sine identity to get the value for $y_{ab}$: $$y_{ab}=a\sin⁡(\alpha)=a\sqrt{1-\cos^2(\alpha)}=a\sqrt{1-\left(\frac{a^2+c^2-b^2}{2ab}\right)^2}$$ but I would like to find a $rational$ solution (without the square root) like the cosine function I used for $x_{ab}$ (if one exists). Can the law(s) of sines (or cosines) be manipulated to produce a sine value using only side lengths without the radical?

poetasis
  • 6,338
  • Not an answer at all but perhaps helpful for the underling problem. https://math.stackexchange.com/questions/2184038/area-of-an-acute-triangle-given-two-sides-and-an-altitude/2184085#2184085 – Ethan Bolker Dec 09 '18 at 16:19
  • Your quest seems not-unlike wanting to find roots of polynomials without encountering imaginary values. Imaginaries are inevitable across the entire family of polynomials, so it's impossible to satisfy the restriction. Even when the roots are real, sometimes you have to pass through imaginaries to get at them. (This is historically why imaginary numbers had to be taken seriously.) Now, there's certainly some subset of polynomials that are solvable without $i$. It may well be that the angles you're studying have rational sines and cosines; you need to describe those angles to be sure. – Blue Dec 13 '18 at 23:10
  • @ Blue I found temporary imaginaries from some inputs after solving a cubic equation. I used De Moivre's Theorem and the imaginaries canceled. What I am hoping for is something like the sine value(s) you showed me in your answer to another question I asked. Still, we do not Know the altitude of triangle that the angle spans here. I seems, however, if all sides and the [spanned-by-angle] altitude is rational, then the sine will be rational. And, perhaps irrational altitudes will cancel when squared. – poetasis Dec 14 '18 at 21:16
  • @ Blue For a paper I am writing,I developed $new$ formulae for the generation of Pythagorean triplets and for matching sides or proving they to not exist. I used them in a program to generate the Isosceles triangle [made of 6 dissimilar $triplets$] that you helped me with. I have also generated triangular pyramids and I hope to use rational numbers until the last operation of the calculation of altitudes. – poetasis Dec 14 '18 at 21:37

3 Answers3

3

This is possible only for acute triangles of a special type.

For example, a triangle with sides $a=10,\ b=17,\ c=21$ can be constructed as follows.

Let $n = 2$ and $c\in Ox.$ Then: $$a = 2(2^{2n-2}+1) = 10,\quad a_x = 2(2^{2n-2}-1) = 6,\quad a_y= 2^{n+1}=8,$$ $$b = 2^{2n}+1 = 17,\quad b_x = 2^{2n}-1 = 15,\quad b_y = a_y=8,\quad c = a_x+b_x = 21,$$ wherein $$\sin(\alpha)=\dfrac {a_y}{a} = \dfrac45,\quad \cos(\alpha)= \dfrac{a_x}{a} = \dfrac35,$$ $$\quad \sin(\beta) = \dfrac{b_y}{b} = \dfrac8{17},\quad \cos(\beta)=\dfrac{b_x}{b} = \dfrac{15}{17}.$$

The reason is that for any $n\geq 2,\quad k=0\dots n-1$ there are Pythagorean triples with the sides $2^k(2^{2n-2k}\pm1)$ and with the common branch $2^{n+1}.$

More interesting examples can be constructed using known Pythagorean triples.
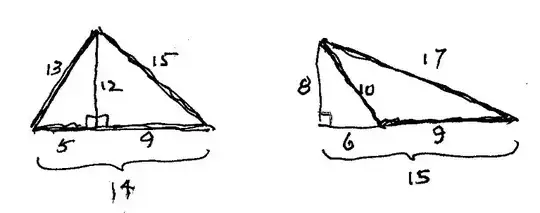
Some of them are given in the table below $$\begin{vmatrix} a & a_x & a_y=b_y & b & b_x & c= a_x+b_x\\ 13 & 5 & 12 & 15 & 9 & 14\\ 13 & 5 & 12 & 20 & 16 & 21\\ 26 & 10 & 24 & 25 & 7 & 17\\ 25 & 7 & 24 & 30 & 18 & 25\\ 5 & \dfrac75 & \dfrac{24}5 & 6 & \dfrac{18}5 & 5\\ \end{vmatrix}$$

$$\color{brown}{\textbf{About triangle calculation}}.$$

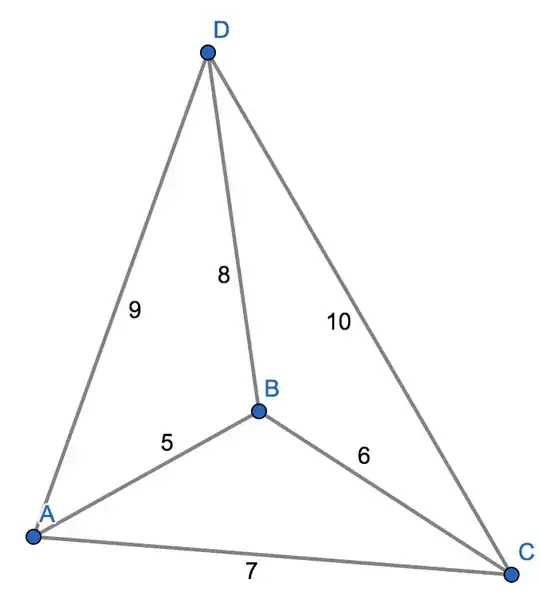
Let $a=5,\ b=6,\ c=7,\ t=a_x,$ then $$a^2-a_x^2 = b^2-b_x^2,$$ $$a^2-t^2 = b^2-(c-t)^2,$$ $$a_x=t=\dfrac{a^2-b^2+c^2}{2c} = \dfrac{19}7,\quad b_x= c-t = \dfrac{30}7,$$ $$a_y=b_y=\sqrt{a^2-a_x^2}=\sqrt{b^2-b_x^2}=\dfrac{12}7\sqrt6,$$ $$A=(0,0),\ B=(a_x, a_y) = \left(\dfrac{19}7,\dfrac{12}7\sqrt6\right),\ C=(0,c)=(0,7).$$ pyramid

$$\color{brown}{\textbf{About triangular pyramid calculation (earlier question)}}.$$

Let $$l_A=AD=9,\ l_B=BD=8,\ l_C=CD=10,\ x=D_x,\ y=D_y,\ h=D_z.$$ Then $$l_A^2-(x^2+y^2) = l_B^2 - ((x-a_x)^2+(y-a_y)^2) = l_C^2 - ((c-x)^2+y^2)=h^2,$$ $$\begin{cases} 2a_xx+2a_yy = l_A^2 -l_B^2 + a^2\\[4pt] 2cx=l_A^2-l_C^2+c^2\\[4pt] h=\sqrt{l_A^2-(x^2+y^2)} \end{cases}\rightarrow \begin{cases} x=\dfrac{l_A^2-l_C^2+c^2}{2c} = \dfrac{15}7\\[4pt] y = \dfrac{l_A^2 -l_B^2 + a^2 -2a_xx}{2a_y} = \dfrac{81-64+25-570/49}{\dfrac{24}7\sqrt6} = \dfrac{31}{21}\sqrt6\\[4pt] h=\sqrt{l_A^2-x^2-\dfrac{\left(l_A^2 -l_B^2 + a^2 -2a_xx\right)^2}{4(a^2-a_x^2)}} = \color{brown}{\sqrt{\dfrac{190}{3}}} \end{cases}$$ (see also Wolfram Alpha).

And trigonometry is not needed.

Yuri Negometyanov
  • 28,026
  • I suggested this in a comment on the original question, before the bounty: https://math.stackexchange.com/questions/2184038/area-of-an-acute-triangle-given-two-sides-and-an-altitude/2184085#2184085 – Ethan Bolker Dec 13 '18 at 23:25
  • @EthanBolker There are too much variants, but $13-14-15$ looks nice. – Yuri Negometyanov Dec 13 '18 at 23:32
  • @EthanBolker I've found $5-6-5$ :) – Yuri Negometyanov Dec 14 '18 at 00:07
  • Sure. Isosceles is easy - two copies of any integral right triangle. – Ethan Bolker Dec 14 '18 at 00:09
  • @EthanBolker You're right, of course. But this is another, non-trivial way. – Yuri Negometyanov Dec 14 '18 at 00:15
  • If I knew the altitude, I would not ask this question. This about finding a rational sine in order to $find$ the altitude. I will be searching thousands or millions of irregular [sometimes Isosceles] triangles programmatically as part of another project that will not use a square root until the last operation. Lacking infinite precision, the only way I can be sure if I find integers in the last operation is to make sure I use rational intermediate numbers. – poetasis Dec 14 '18 at 21:45
  • @Yuri Negometyanov Would this work with, for example, $a=b=2600$, $c=1456$? – poetasis Dec 14 '18 at 21:52
  • @Yuri Negometyanov How about $a=6146410$, $b=8492650$, $5756650$? This is just one of the myriad triangles i will be checking for another project and I want strictly rational coordinates if I can get them. – poetasis Dec 14 '18 at 22:02
  • @Yuri Negometyanov Parden my fat fingers; in the above,$c=5756650$. – poetasis Dec 14 '18 at 22:09
  • @poetasis See updated answer. What do you think about? – Yuri Negometyanov Dec 14 '18 at 23:04
2

Call a triangle rational if the sines and cosines of all three of its angles are rational.

What follows shows that you build rational triangles by gluing together rational right triangles (scaled Pythagorean triples) along a common edge. For example, $13,14,15$ and $9,10,17$:

enter image description here

Lemma. Rationality is scale invariant. The sides of rational triangle are commensurate. A rational triangle is always similar to a rational triangle with integer sides;

Proof: Scale invariance is obvious. For the second assertion use the law of sines. For the third, find the least common multiple of the denominators.

Lemma. A triangle is rational if two of its three angles have rational sine and cosine.

Proof: Use the fact that the sum of the angles is $\pi$ and the addition formulas for sine and cosine to calculate the sine and cosine of the third angle.

Corollary. A right triangle is rational if and only if it's similar to a Pythagorean triangle (a right triangle with integer sides).

Theorem. A triangle is rational if and only if each of the triangles formed by dropping an altitude from a vertex is a Pythagorean triangle.

Proof. Put together the pieces. Note that you can use any one of the three altitudes.

So there are lots of rational triangles, with many shapes, obtuse as well as acute, scalable if you don't require integer side lengths. I am pretty sure that rational triangles are dense in the space of all triangles, with just about any measure of the distance between triangles.

Note. It was fun to take up this question after more than $60$ years: Area of an acute triangle, given two sides and an altitude

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
-1

I think I would look for the intersection of the cricles

$x^2 + y^2 = 25\\ (x-7)^2 + y^2 = 36\\ x^2 -14x + 49 + y^2 = 36\\ x^2 - 14x + y^2 = -13$

Subtract the last line from the first line.

$14x = 38\\ x = \frac {38}{14}$

And substitute into either equation

$\frac {38^2}{14^2} + y^2 = 25\\ y^2 = \frac {4900 - 1444}{196}\\ y = \frac {\sqrt {3456}}{14}\\ y = \frac {12\sqrt {6}}{7}$

Doug M
  • 57,877
  • I''m not looking for the sine of $this$ triangle. I'm looking for a sine formula that uses just the sides of an acute triangle $without$ a square root. The emphasis is that the result must be strictly rational. Alternatively, if you can convince me that such does not exist, that would be worth something too. – poetasis Dec 13 '18 at 19:52
  • since 7 is not a Gaussian integer, it restricts the number of rotations such that the endpoints will be rational numbers. And for all of these rotations, the 3rd vertex will be at an irrational number. – Doug M Dec 13 '18 at 20:18
  • The triangle in the question was only for demo purposes. The triangles I'm searching may have sides of hundreds or thousands of units. – poetasis Dec 13 '18 at 20:55