1

There a many questions about this Theorem: There is no set of all sets. But I have not found a proof of it using first-order logic. I follow the Textbook Ciesielski, 1997, that has a proof with plain English.

My understanding: If we define $\varphi(x)=\neg(x\in x)$, and we apply the schema of separation: $\forall z\exists y\forall x[x\in y\Leftrightarrow (x\in z\land \varphi(x))]$, we should get some contradiction.

Is my understanding correct? Is the proof difficult?

I studied the rudiments of Propositional Logic (incl. Soundness and Completeness), but for FOL I just finished the syntax.

EDIT 1

Ciesielski introduce the Theorem above with the following words: An interesting consequence of the comprehension scheme [meaning the schema of separation as synonym] axiom is the following theorem. Is he wrong?

PeptideChain
  • 829
  • Separation can create sets from bigger sets. What you need is regularity. – SK19 Jun 02 '18 at 21:14
  • ChristopherMarley, @sk19 : see my edit – PeptideChain Jun 02 '18 at 21:19
  • The proof is correct - if you have the comprehension scheme, from existence of the set of all sets you can deduce existence of Russell's paradoxical set. No need for regularity axiom (though using regularity you can give a different proof that there is no set of all sets). – Wojowu Jun 02 '18 at 21:24
  • 1
    @ChristopherMarley While that works in ZF, you don't in fact need to use the axiom of foundation/regularity at all here, and since there are interesting set theories where it fails it's a good idea not to. – Noah Schweber Jun 02 '18 at 21:32

2 Answers2

3

This is just Russell's paradox. Suppose there were a set of all sets, $U$. By separation, we get $$R=\{x\in U: x\not\in x\}.$$ Since $U$ contains all sets, we have that the "$\in U$" can be omitted: $$R=\{x: x\not\in x\}.$$ That is, we have

$\forall x(x\in R\iff x\not\in x)$.

But now consider taking $x=R$: we get $R\in R\iff R\not\in R$, which is a contradiction.

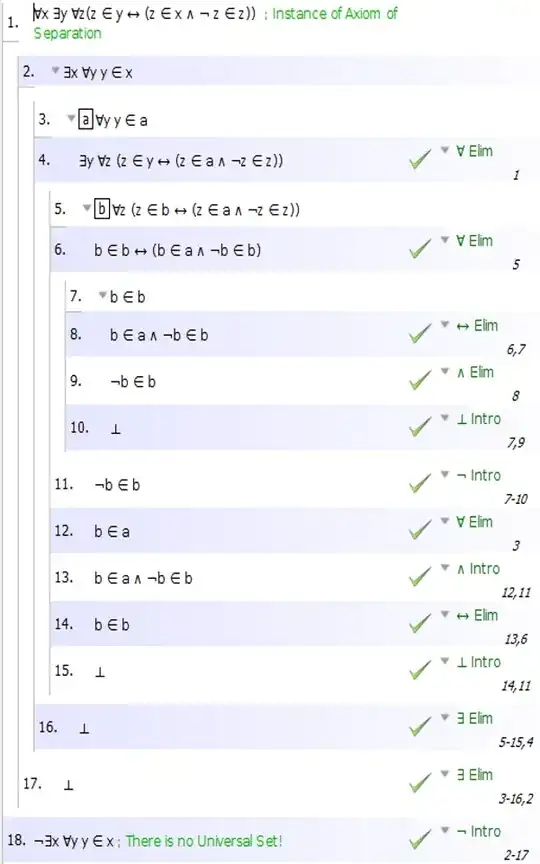
To formalize this in first-order logic, here are the key things you'll need to prove:

  • $\forall x\exists y\forall z(z\in y\iff z\in x\wedge z\not\in z)$. This is an instance of separation: "for each set $x$, the set $\{z\in x: z\not\in z\}$ is a set."

  • $\forall x[\forall y(y\in x)\implies \forall y((\forall z(z\in y\iff z\in x\wedge z\not\in z))\implies (\forall z(z\in y\iff z\not\in z)))]$. Basically, if $x$ is the universal set then the set of elements of $x$ not containing themselves is in fact the set of all sets not containing themselves.

  • $(\exists x\forall y(y\in x))\implies (\exists x\forall y(y\in x\iff y\not\in y))$. If there is a set of all sets, then there is a set of all sets not containing themselves.

  • $\forall x[(\forall y(y\in x\iff y\not\in y))\implies (x\in x\iff x\not\in x)]$. If there is a set of all sets not containing themselves, we get a contradiction.

No particular step here is hard, but if you're really doing a completely formal deduction it will be a bit tedious. The key bulletpoint is the second one (the first is an immediate application of separation, the third follows from the first and second, and the fourth is just unwinding the definitions). The second bulletpoint is intuitively true since, if $x$ is a universal set, then the formulas "$z\not\in z$" and "$z\in x\wedge z\not\in z$" are equivalent; now you need to figure out how to put that equivalence "inside" some quantifiers in the appropriate way.

Noah Schweber
  • 245,398
2

Here is a formal proof in Fitch:

enter image description here

Bram28
  • 100,612
  • 6
  • 70
  • 118
  • I've a new question, I'm sure it is peanuts for you: here – PeptideChain Jun 08 '18 at 10:16
  • @LiPo The question is closed ... if you still want a FOL proof you'll need to try and reopen it (you can say that you asked for a formal proof, not just a mathematical proof) – Bram28 Jun 08 '18 at 12:41
  • do you have one? sure, I'm interested in it! – PeptideChain Jun 08 '18 at 16:01
  • @LiPo Yes, but it's almost 40 lines long ... not sure I can get that into one screen shot ... Also, this is really a different question warranting a different post. Too bad that other one got closed but like I said, you could appeal to get it opened back up again ... or just create a new post making clear you want a formal proof. Actually, that would work: if you ask one for why you can't have any set contain itself as an element (i.e. that it has to be true that $A \notin A$), I have a 25 line proof for that and the 40 line proof with the two sets really follows the same general idea. – Bram28 Jun 08 '18 at 16:08
  • the first option has given results – PeptideChain Jun 08 '18 at 16:38
  • @LiPo Actually, just thought of something: I can post the proof as an answer to one of the older questions that were being referred when your question was closed ... – Bram28 Jun 08 '18 at 16:42
  • the question should be open/reopened now – PeptideChain Jun 08 '18 at 16:50
  • Let us continue this discussion in chat. – Bram28 Jun 08 '18 at 17:00