-3

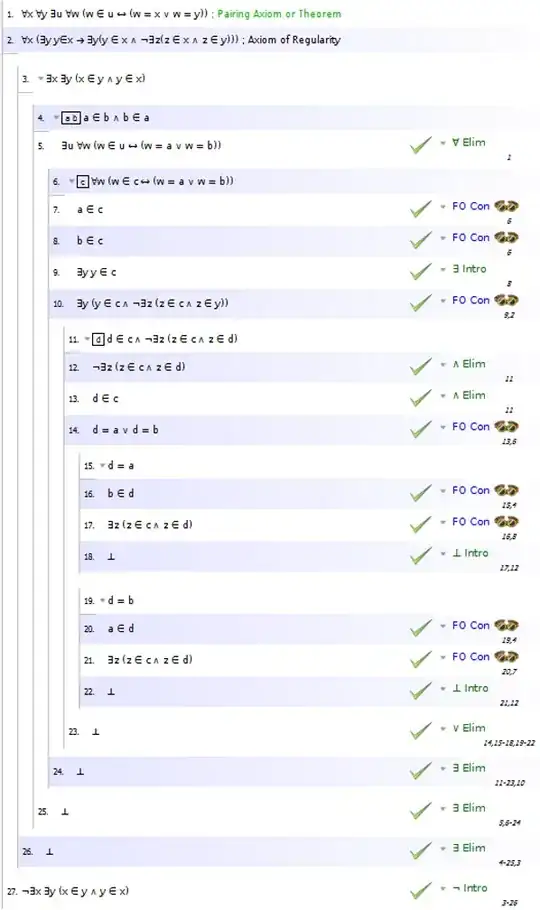
I want to proof that $$\tag{*}(x\in y\land y\in x)\to\bot$$ in First-Order Logic.

Being $x\in y\land y\in x$ cyclic, it is an infinitely-descending $\in$-chain. Such a thing is excluded in ZFC by the axiom of foundation/regularity (see "axiom of foundation and infinite sets").

Here the mentioned axiom: $$\forall x \left[\exists y(y\in x)\to \exists y\left(y\in x\land \neg\exists z\left( z\in x\land z\in y\right)\right)\right],$$ or $$\forall x\,(x\neq \varnothing \rightarrow \exists y\in x\,(y\cap x=\varnothing )).\tag{**}$$

The example $x=\{y\}$ and $y=\{x\}$ satisfies (**), doesn't it?

EDIT

I would like my question to be reopened because, although the question Prove that for any two sets $A$ and $B$, $A\notin B$ or $B\notin A$ is similar in content, I would like a formal proof as is mentioned in the title (or I thought to mention by specifying FOL). It is not about understanding (the answer to the other question is perfect, actually the comment to this question was enough to understand), but about the formal proof. Thank you.

Shaun
  • 44,997
PeptideChain
  • 829

1 Answers1

1

Here is a proof in Fitch ... the FO Con steps are computer-assisted steps but are easily fleshed out into actual formal inference rules. The $c$ introduced on line $6$ is of course the set $\{ a, b \}$ (= $\{ x, y \}$ in your question)

enter image description here

Bram28
  • 100,612
  • 6
  • 70
  • 118
  • 1
    Please don't insert images of the results generated by a computer program. It's like going to Wolfram to ask for a solution to a specific integral, with step-by-step instructions, copying the image, or a screenshot, and uploading it in an answer post. Here and there, occasionally, I can understand its use. But this program is your go-to for proofs these days. For future users' sake, please explain in more detail what the shorthand justifications stands for. – amWhy Jun 08 '18 at 20:09