Spectral densities of finite dimensional sample covariance matrices

Question

Let $N \ge 2$ and $T > N$ be integers.

In multivariate statistics it is of interest to analyze spectra of sample covariance matrices. The resolvent ${\mathfrak g}_M(z)$ encapsulates the whole information about the distribution of eigenvalues of the underlying covariance matrix. We have: \begin{equation} {\mathfrak g}_M(z):= \frac{1}{N} \left< Tr\left[ (z{\bf 1}- {\bf M} )^{-1} \right] \right> \end{equation} where $M:= 1/T \cdot (\tilde{C} X \cdot X^T \tilde{C}^T)$ and $X$ is a $N\times T$ matrix whose elements are independent, identically distributed sampled from a standardized Gaussian distribution and $\tilde{C} \cdot \tilde{C}^T = C$ . The matrix $M$ is a sample covariance matrix in a Gaussian population subject with the underlying covariance matrix being equal to $C$. It is well known that the probability density function of the eigenvalues of $M$ is given as an inverse Stieltjes transform of the resolvent. We have: \begin{equation} \rho(\lambda) = \lim_{\epsilon \rightarrow 0} \frac{1}{\pi} Im {\mathfrak g}_M(\lambda-\imath \epsilon) \end{equation}

Now, by using Symbolic inverse of a linear combination of two matrices and the parametrization of the orthogonal group given in here Itzykson-Zuber integral over orthogonal groups we computed the spectral density in case $N=2$ and the underlying covariance matrix being an identity $C=1$. We have: \begin{eqnarray} {\mathfrak g}_M(z) &=& \frac{1}{N} Tr\left[\left< \frac{(z-a_1) {\bf 1} + {\bf M}}{z^2-a_1 z+a_2} \right> \right]\\ &=& {\mathfrak N}_{2,T} \cdot (2\pi)\int\limits_{{\mathbb R}^2} \frac{(z-a_1) 1+ a_1/2}{z^2-a_1 z+a_2} \cdot \left| \nu_1-\nu_2 \right| \cdot (\nu_1 \nu_2)^{(T-3)/2} e^{-T/2(\nu_1+\nu_2)} d\nu_1 d\nu_2 \\ &=& {\mathfrak N}_{2,T}\cdot (2\pi)\int\limits_{0 < \nu_1 < \nu_2 < \infty} \left[ \frac{1}{z-\nu_1} + \frac{1}{z-\nu_2} \right] (\nu_2-\nu_1) \cdot (\nu_1 \nu_2)^{(T-3)/2} e^{-T/2(\nu_1+\nu_2)} d\nu_1 d\nu_2 \end{eqnarray} where $a_1:=Tr({\bf M})$ and $a_2:=\det({\bf M})$ are the rotational invariants of matrix ${\bf M}$. Here the constant ${\mathfrak N}_{2,T}$ is the normalization factor of the Wishart distribution and it reads: \begin{equation} {\mathfrak N}_{2,T}:=(\frac{T}{2})^T \cdot \frac{1}{\sqrt{\pi} \Gamma(T/2) \Gamma((T-1)/2)} \end{equation} see equation (1.7) page 7 in https://arxiv.org/abs/1610.08104 for example.

Now, by taking the inverse Stieltjes transform we get the spectral density as follows: \begin{eqnarray} &&\rho_{2,T}(z) = {\mathfrak N}_{2,T}\cdot (2\pi)\\ &&\int\limits_{0 < \nu_1 < \nu_2 < \infty} \left[ \delta(z-\nu_1) + \delta(z-\nu_2) \right] (\nu_2-\nu_1) \cdot (\nu_1 \nu_2)^{(T-3)/2} e^{-T/2(\nu_1+\nu_2)} d\nu_1 d\nu_2 \end{eqnarray} The integral above is pretty simple to evaluate and the result reads: \begin{eqnarray} &&\rho_{2,T}(z) dz =\\ && \frac{\sqrt{\pi}}{2 \Gamma(\frac{T}{2}) \Gamma(\frac{(T-1)}{2})} \cdot u^{\frac{T-3}{2}} e^{-u} \left[2\Gamma(\frac{T+1}{2},u)- \Gamma(\frac{T+1}{2}) - 2 u \Gamma(\frac{T-1}{2},u)+u \Gamma(\frac{T-1}{2})\right] du \end{eqnarray} where $u:=z\cdot T/2$. From the above we calculate the spectral moments: \begin{eqnarray} \left< \lambda^p \right> &=& \frac{T^{(p)}}{T^p} \cdot \frac{p \left(\, _2F_1\left(1,p+T;\frac{T+1}{2};\frac{1}{2}\right)-\, _2F_1\left(1,p+T;p+\frac{T+1}{2};\frac{1}{2}\right)\right)+2 (p+T-1)}{2 (2 p+T-1)}\\ &=& \frac{T^{(p)}}{T^p} \cdot \left( 1+\frac{p}{T+2 p-1} \sum\limits_{k=1}^{p-1} (-1)^k \frac{((1-T)/2-p)^{(k)}}{((T+1)/2)^{(k)}}\right)\\ &=&\frac{1}{T^p}\cdot \left(\prod\limits_{j=0}^{p-1} (T+j) + p \sum\limits_{k=1}^{p-1} \prod\limits_{j=k\wedge p-k}^{\lfloor p/2 \rfloor -1}(T+1+2 j) \cdot \prod\limits_{j=0}^{\lceil p/2 \rceil -1} (T+2 j) \cdot \prod\limits_{j=k\vee p-k}^{p-2} (T+1+2 j)\right)\\ &=& 1+ \sum\limits_{m=1}^{p-1} \frac{1}{T^m} \cdot a_m^{(p)} \cdot \binom{p}{m+1}\\ &=&\left\{ \begin{array}{c} 1\\1\\\frac{3}{T}+1\\\frac{14}{T^2}+\frac{9}{T}+1\\\frac{94}{T^3}+\frac{79}{T^2}+\frac{18}{T}+1\\\frac{824}{T^4}+\frac{810}{T^3}+\frac{255}{T^2}+\frac{30}{T}+1\\\frac{8904}{T^5}+\frac{9742}{T^4}+\frac{3723}{T^3}+\frac{625}{ T^2}+\frac{45}{T}+1\\ \vdots \end{array} \right\} \end{eqnarray} where in the second line from the top we used http://functions.wolfram.com/HypergeometricFunctions/Hypergeometric2F1/03/04/04/ . Here $p\in {\mathbb N}$.

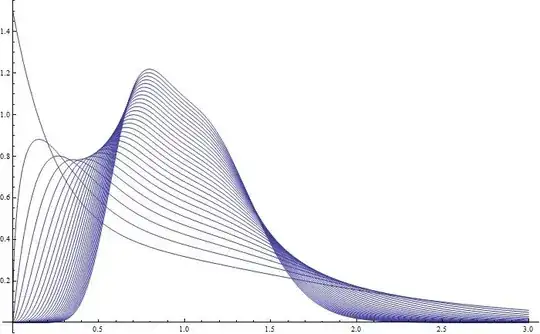
Here: \begin{eqnarray} a_m^{(p)} := \left\{ \begin{array}{rr} 3 & \mbox{if $m=1$}\\ \frac{1}{4}(-13+23 p) & \mbox{if $m=2$}\\ \frac{1}{10}(-8+7p)(-5+13 p) & \mbox{if $m=3$}\\ \frac{1}{336} (p (p (4353 p-12386)+8811)-1666) & \mbox{if $m=4$}\\ \frac{1}{336} (p (p (p (5797 p-26118)+33443)-14274)+2016) & \mbox{if $m=5$}\\ \vdots \end{array} \right. \end{eqnarray} Below we plot the spectral density for $T=3,\cdots,30$.

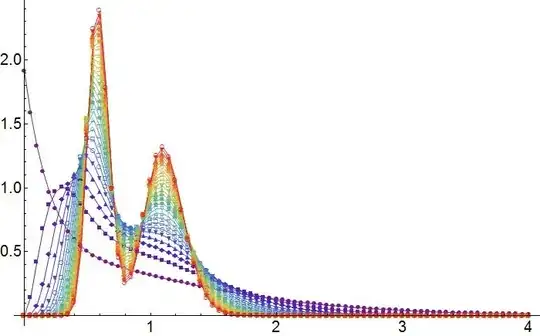
We also checked by Monte Carlo simulation that the closed form expression above matches well the simulation histogram.

Now my question is twofold.

Firstly, can we derive a closed form expression for the spectral density for arbitrary $N \ge 2$ and for $C=1$?

Secondly, can we generalize the obtained expression and get the naswer for an arbitrary positive definite and symmetric matrix $C$?

Note that having got the expression in question we can always take the limit $\rightarrow \infty$ subject to $N/T=q= \mbox{const}$ and obtain the Marchenko-Pastur Law(MPL) which in case of the underlying covariance matrix being identity reads: \begin{eqnarray} \lim\limits_{N \rightarrow \infty} \rho_{N,\frac{N}{q}}(z) = \frac{1}{2\pi} \cdot \frac{\sqrt{(z_+-z)(z-z_-)}}{q z} \end{eqnarray} where $z_\pm:=1\pm \sqrt{q}$.

Answer 1

Here we provide an answer in case $n=2$. Here the underlying covariance matrix reads: \begin{equation} C = \left( \begin{array}{rr} c_{1,1} & \rho \\ \rho & c_{2,2}\end{array} \right) \end{equation} and has eigenvalues $\lambda_{1,2}=1/2\left( Tr(C) \pm \sqrt{Tr(C)^2-4 \det(C)}\right)$ .

The normalized trace of the resolvent reads: \begin{eqnarray} &&{\mathfrak g}_M(z) = \int\limits_0^{2 \pi} \int\limits_{0 < \nu_1 < \nu_2< \infty} \left[ \frac{1}{z-\nu_1} + \frac{1}{z-\nu_2} \right] \cdot \\ && \underbrace{(\nu_2-\nu_1)}_{I_1} \cdot \underbrace{{\mathfrak N}_{2,T} \frac{(\nu_1 \nu_2)^{\frac{T-3}{2}}}{(\lambda_1 \lambda_2)^{\frac{T}{2}}} e^{-\frac{T}{2} Tr\left[C^{-1} \cdot O \cdot \left(\begin{array}{rr} \nu_1 & 0 \\ 0 & \nu_2\end{array} \right) \cdot O^T \right]}}_{I_2} d\nu_1d\nu_2 \cdot d\phi \end{eqnarray}

Now, the quantity $I_2$ is the Wishart probability density function or, in other words, it is the Jacobian of the mapping $\left\{ X_{i,t} \right\}_{i=1,t=1}^{2,T} \longrightarrow \left\{ M_{i,j} \right\}_{1\le i \le j \le 2}$ from the returns to the elements of the sample covariance matrix. On the other hand the quantity $I_1$ is the Jacobian of the mapping $\left\{ M_{i,j}\right\}_{1\le i \le j \le 2} \longrightarrow \left\{\nu_1,\nu_2;\phi\right\}$ from the elements of the sample covariance matrix to the eigenvalues and to the angle that determines the eigenvectors. Here \begin{equation} O:=\left( \begin{array}{rr} \cos(\phi) & -\sin(\phi) \\ \sin(\phi) & \cos(\phi)\end{array}\right) \end{equation}

Now, a simple calculation shows the following: \begin{eqnarray} &&Tr\left[C^{-1} \cdot O \cdot \left(\begin{array}{rr} \nu_1 & 0 \\ 0 & \nu_2\end{array} \right) \cdot O^T \right] = \\ &&\frac{1}{2} \frac{Tr(C)}{\det(C)}(\nu_1+\nu_2) - \frac{1}{2}\frac{(c_{1,1}-c_{2,2})}{\det(C)}(\nu_1-\nu_2) \cos(2 \phi) - \frac{1}{2} \frac{2\rho (\nu_1-\nu_2)}{\det(C)} \sin(2 \phi) \end{eqnarray} Since the above quantity is the only quantity in the integrand that depends on the angle integrating over that angle can be readily done by using Itzykson-Zuber integral over orthogonal groups and leads to the following: \begin{eqnarray} &&{\mathfrak g}_M(z) = {\mathfrak N}_{2,T} (2 \pi) \cdot \\ &&\int\limits_{0 < \nu_1 < \nu_2 < \infty} \frac{1}{2} \left[ \frac{1}{z-\nu_1} + \frac{1}{z-\nu_2}\right] \cdot (\nu_2-\nu_1) \cdot \frac{(\nu_1 \nu_2)^{\frac{T-3}{2}}}{(\lambda_1 \lambda_2)^{\frac{T}{2}}} \cdot e^{-\frac{T}{4} \cdot \frac{Tr(C)}{\det(C)} \cdot (\nu_1+\nu_2)} \cdot I_0\left( (\nu_2-\nu_1) \frac{T}{4} \frac{\sqrt{Tr(C)^2 - 4 \det(C)}}{\det(C)} \right) d\nu_1 d\nu_2 \end{eqnarray} where $I_0()$ is the modified Bessel function of zeroth order.

Now, in order to proceed further we take the inverse Stieltjes transform to get the spectral density. In this process the fractions in the square brackets in the integral over the eigenvalues above turn into Dirac delta functions as follows $1/(z-\nu_\xi) \longrightarrow \delta(z-\nu_\xi)$ for $\xi=1,2$. These Dirac delta functions annihilate one of the integration variables and we end up with two one dimensional integrals. We have: \begin{eqnarray} &&\rho(z) = \frac{{\mathfrak N}_{2,T}}{2(\lambda_1 \lambda_2)^{\frac{T}{2}}} z^{(T-3)/2} e^{\left( -\frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1 \lambda_2} z\right)}\cdot \\ && \left( \int\limits_0^z (z-\nu) \nu^{(T-3)/2} e^{-\frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1 \lambda_2} \nu} I_0\left( (z-\nu) \frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1\lambda_2}\right) d\nu + \int\limits_z^\infty (\nu-z) \nu^{(T-3)/2} e^{-\frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1 \lambda_2} \nu} I_0\left( (\nu-z) \frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1\lambda_2}\right) d\nu \right) \end{eqnarray} Now by using the integral representation of the Bessel function we evaluated the integrals above in "closed form". Firstly we define: \begin{eqnarray} &&f_> (m,z,A,B):=\\ && e^{-A z} \sum\limits_{p=0}^m \frac{m!}{p!} z^p (-1)^{m-p} \sum\limits_{m_2=0}^{\lfloor \frac{m-p}{2} \rfloor} \binom{m-p-m_2}{m_2} \binom{-1/2}{m-p-m_2} \frac{(2 A)^{m-p-2 m_2}}{(A^2-B^2)^{1/2+m-p-m_2}}\\ &&f_\infty(m,z,A,B):=\frac{m!}{2\pi} \int\limits_0^{2 \pi} \frac{e^{z B \sin(\tau)}}{(A+B \sin(\tau))^{m+1}}d\tau \end{eqnarray} and then we have: \begin{eqnarray} &&\rho(z) = \frac{{\mathfrak N}_{2,T}}{2(\lambda_1 \lambda_2)^{\frac{T}{2}}} z^{(T-3)/2} e^{\left( -\frac{T}{4} \frac{\lambda_1+\lambda_2}{\lambda_1 \lambda_2} z\right)}\cdot \\ &&\left(\right.\\ &&\left. z f_\infty(\frac{T-3}{2}, z, \frac{T}{4} \frac{\lambda_2+\lambda_1}{\lambda_1 \lambda_2},\frac{T}{4} \frac{\lambda_2-\lambda_1}{\lambda_1 \lambda_2}) - f_\infty(\frac{T-1}{2}, z, \frac{T}{4} \frac{\lambda_2+\lambda_1}{\lambda_1 \lambda_2},\frac{T}{4} \frac{\lambda_2-\lambda_1}{\lambda_1 \lambda_2})+ \right.\\ && 2f_>(\frac{T-1}{2}, z, \frac{T}{4} \frac{\lambda_2+\lambda_1}{\lambda_1 \lambda_2},\frac{T}{4} \frac{\lambda_2-\lambda_1}{\lambda_1 \lambda_2})-2 zf_>(\frac{T-3}{2}, z, \frac{T}{4} \frac{\lambda_2+\lambda_1}{\lambda_1 \lambda_2},\frac{T}{4} \frac{\lambda_2-\lambda_1}{\lambda_1 \lambda_2})\\ &&\left.\right) \end{eqnarray}

Below I plot the spectral densities for $T=3,5,7,\cdots,103$ (Violet, Blue all the way through to Red). We have:

Here $(\lambda_1,\lambda_2)=(0.60735,1.10567)$ .