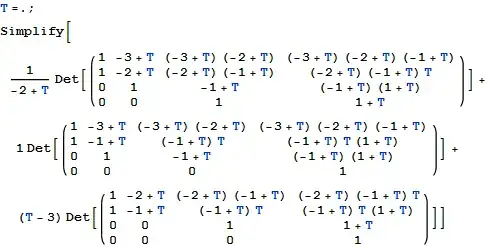Let $d \in 2{\mathbb N}$ be an even positive integer, let $p\in {\mathbb N}$ be another positive integer and let $T$ be a parameter. Let $\vec{q} := \left( q_\xi \right)_{\xi=0}^{d/2-1} \in {\mathbb N}^{(d/2)}$. Consider a following multiple sum: \begin{eqnarray} &&{\mathcal S}_{d,p}(T):=\sum\limits_{j=1}^d \sum\limits_{2 \le q_0 \le \cdots \le q_{d/2-1} \le d} \frac{1}{2^{|\vec{q}|} \cdot \nu(\vec{q})} \left| \begin{array}{r} \left( (\frac{T-d-1}{2} + \delta_{2 \xi+1,j} p+q_\xi)^{(\eta-q_\xi)} 1_{q_\xi \le \eta}\right)_{\eta=1}^d\\ \left(2^{-\eta+1} (T-d+1)^{(p(\delta_{2\xi+1,j}+\delta_{2\xi+2,j})+\eta+q_\xi-3)}\right)_{\eta=1}^d\\ \end{array} \right|_{\xi=0}^{d/2-1} \end{eqnarray} where $\nu(\vec{q}) := \prod_{\eta=2}^d p_\eta!$ where \begin{equation} \vec{q}:= \left( \underbrace{2,\cdots,2}_{p_2}, \underbrace{3,\cdots,3}_{p_3}, \cdots, \underbrace{d,\cdots,d}_{p_d} \right) \end{equation} Note that the term in the multiple sum is a determinant of a $d\times d$ matrix whose entries are polynomials in $T$. We stumbled across this sum when solving question Spectral densities of finite dimensional sample covariance matrices .
Now by using Mathematica we have discovered the following pattern: \begin{equation} {\mathcal S}_{d,p}(T)= \sum\limits_{\xi=0}^{(2d-5) \vee 0} (T-d+1)^{(p+\xi)} \cdot P_{d,\xi}^{(\frac{d^2}{4}-1-\xi)}(T) \end{equation} where $P_{d,\xi}^{(\frac{d^2}{4}-1-\xi)}(T)$ is a polynomial in $T$ of order $(\frac{d^2}{4}-1-\xi)$.
Here the polynomials in question read: \begin{eqnarray} P_{2,0}^{(0)}(T) &=& \frac{1}{2}\\ \hline\\ P_{4,0}^{(3)}(T) &=& \frac{1}{128} (T-3) \left(2 p^2 T-2 p^2-p T+3 p+2 T^2-6 T+4\right)\\ P_{4,1}^{(2)}(T) &=& \frac{1}{128} \left(-4 p^2 T+8 p^2-3 p T+5 p-2 T^2+10 T-12\right)\\ P_{4,2}^{(1)}(T) &=& \frac{1}{64} \left(p^2+2 p-T+3\right)\\ P_{4,3}^{(0)}(T) &=& \frac{1}{64}\\ \hline\\ \vdots \end{eqnarray}
Now my question will be how do we find a closed form expression for the polynomials in question for arbitrary $d$.
Update: Note that we also have: \begin{eqnarray} {\mathcal S}_{d,0}(T) &=& d \cdot 2^{-1-\frac{d^2}{4}}\prod\limits_{j=0}^{d/2-1} (T-d+1)^{(d-2 j-2)} (\frac{1}{2})^{(j)} j!\\ &=& d \cdot 2^{-1-\frac{d^2}{4}} \left(\prod\limits_{j=0}^{d/2-1} (\frac{1}{2})^{(j)}j!\right) \cdot \prod\limits_{k=2}^{d-1} (T-k)^{\lfloor \frac{k}{2}\rfloor} \end{eqnarray}
Below is a piece of Mathematica code that "proves" the above relationship.
d = 2 RandomInteger[{1, 5}]; T =.; p = 0;
mat = Flatten[
Table[{Table[q[xi], {xi, 0, d/2 - 1}], (-1)^(d/2) 1/2^
Sum[q[xi], {xi,
0, (d)/2 -
1}] 1/(Times @@ (Tally[Table[q[xi], {xi, 0, d/2 - 1}]][[All,
2]]!))
Sum[Det[
Riffle[
Table[Pochhammer[(T - d - 1)/2 + KD[2 xi + 1, j] p +
q[xi], (eta - q[xi])] If[q[xi] <= eta, 1, 0], {xi, 0,
d/2 - 1}, {eta, 1, d}],
Table[1/2^(eta - 1)
Pochhammer[T - d + 1,
p (KD[2 xi + 1, j] + KD[2 xi + 2, j]) + eta - 1 + q[xi] -
2], {xi, 0, d/2 - 1}, {eta, 1, d}]]
], {j, 1, d}]}
, Evaluate[
Sequence @@
Join[{},
Table[{q[xi], If[xi == 0, 2, q[xi - 1] + 1], d}, {xi, 0,
d/2 - 1}]]]], d/2 - 1];
(Total[mat[[All, 2]]] - (d Product[
Pochhammer[T - d + 1, d - 2 j - 2] Pochhammer[1/2, j] (j)!, {j,
0, d/2 - 1}] 2^(-1 - d^2/4))) // Simplify
MatrixForm[mat]
Again, my question is how do we go about proving this relationship rigorously.
Update 2: By simplifying the relationship in Update 1 we end up with a following different relationship: \begin{eqnarray} &&\sum\limits_{2 \le q_0 < \cdots < q_{d/2-1} \le d} (-1)^{d^2/2} \prod\limits_{j=-d+1}^{-2} \left[ \frac{(T+j)^{\sum\limits_{\xi=0}^{d/2-1} 1_{-2 \xi-1 \le j \le q_\xi-d-2} \cdot 1_{q_\xi\ge d-2 \xi}}} {(T+j)^{\sum\limits_{\xi=0}^{d/2-1} 1_{q_\xi-d-1 \le j \le -2\xi-2} \cdot 1_{q_\xi\le d-2 \xi}}} \right] \cdot \left| \begin{array}{r} \left(\prod\limits_{j=q_\xi}^{q_\xi+\eta-2}(T-d-1+1 \cdot j)\right)_{\eta=1}^d\\ \left(\prod\limits_{j=q_\xi}^{\eta-1} (T-d-1+2 \cdot j)1_{q_\xi \le \eta}\right)_{\eta=1}^d \end{array} \right|_{\xi=0}^{d/2-1} =\\ &&2^{\frac{d^2}{4}-1} \cdot \prod\limits_{\xi=0}^{d/2-1} (\frac{1}{2})^{(\xi)} \xi! \end{eqnarray}
For example if we take $d=4$ the left hand side reads:
which is independent of $T$ and reads $-4$.
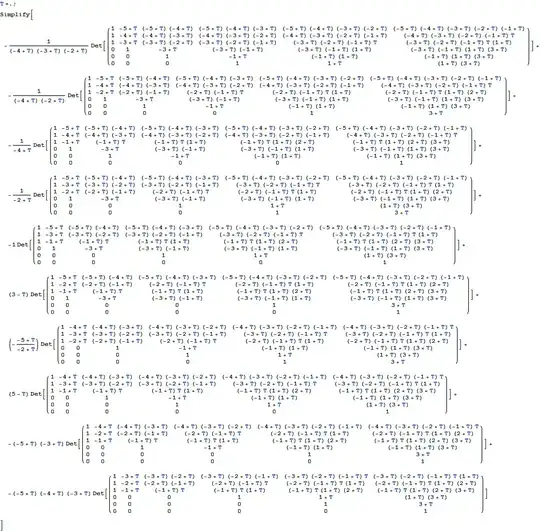
Likewise for $d=6$ the left hand side reads:
which again is independent of $T$ and reads $192$.
Now, again how do we prove that relationship rigorously?