Riemann zeta for real argument between 0 and 1 using Mellin, with short asymptotic expansion

Question

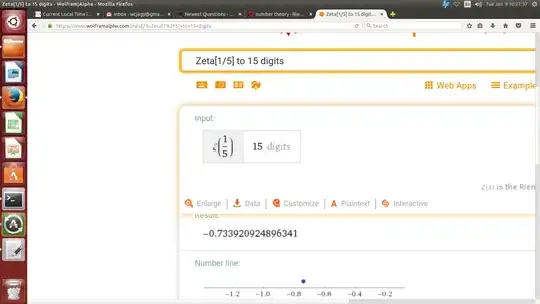
The following would appear to be true.

For real $0 < \sigma < 1,$ we seem to have a very satisfying sum minus integral limit, $$ \zeta(\sigma) \; \; = \; \; \lim_{n \rightarrow \infty} \; \; \left( \sum_{k=1}^n \frac{1}{k^\sigma} \right) - \frac{n^{1-\sigma}}{1-\sigma} \; \; . $$

A little more detail in these examples:

$$ \lim_{n \rightarrow \infty} \; \; \left( \sum_{k=1}^n \frac{1}{\sqrt k} \right) - 2 \sqrt n - \frac{1}{2 \sqrt n} + \frac{1}{24 n^{3/2}} \; \; = \; \; \zeta \left(\frac{1}{2}\right) \approx -1.460354508809586 $$

$$ \lim_{n \rightarrow \infty} \; \; \left( \sum_{k=1}^n \frac{1}{\sqrt[3] k} \right) - \frac{3 n^{2/3}}{2} - \frac{1}{2 \sqrt[3] n} + \frac{1}{36 n^{4/3}} \; \; = \; \; \zeta \left(\frac{1}{3}\right) \approx -0.973360248350782 $$

So, are the above items really really true (rather than wishful thinking), and, if so, given $0 < \sigma < 1,$ what real numbers $A = A(\sigma), B = B(\sigma),$ make the short asymptotic expansion below correct?

$$ \left( \sum_{k=1}^n \frac{1}{k^\sigma} \right) - \frac{n^{1-\sigma}}{1-\sigma} - A n^{-\sigma} + B n^{-1-\sigma} \; \; = \; \; \zeta(\sigma) \; \; + \; \; O(n^{-2-\sigma}) \; \; ? $$

Here is an estimate of $\zeta\left( \frac{1}{5} \right)$ using Daniel's expansion as far as the $3+\sigma$ term, ignoring $5+\sigma$: $$ \zeta(\sigma) =\left( \sum_{k=1}^n \frac{1}{k^\sigma} \right) - \frac{n^{1-\sigma}}{1-\sigma} - \frac{1}{2 n^\sigma} + \frac{\sigma}{12 n^{1 + \sigma}} - \frac{\sigma (1 + \sigma)(2 + \sigma)}{720 n^{3+\sigma}} + O \left( \frac{1}{n^{5 + \sigma}} \right)$$ I think it will let me fit 33 lines in a "code" window without introducing a scroll bar.

    1   1                   -0.7340666666666666   
    2   1.870550563296124   -0.7339263390330826   
    3   2.673292125056355   -0.7339216399387463   
    4   3.431150408311554   -0.7339210905379737   
    5   4.155930071989249   -0.7339209776636304   
    6   4.854757190760828   -0.7339209455319796   
    7   5.532368104161309   -0.7339209342063361   
    8   6.192122059547756   -0.7339209295629763   
    9   6.836516074525011   -0.7339209274322004   
   10   7.467473419005204   -0.7339209263652269   
   11   8.086517339689049   -0.7339209257924113   
   12   8.694881681582254   -0.7339209254668952   
   13   9.293584537123753   -0.7339209252729478   
   14   9.883479099480143   -0.7339209251526775   
   15   10.46528985863283   -0.7339209250754953   
   16   11.03963903613135   -0.7339209250244763   
   17   11.60706632180293   -0.7339209249898626   
   18   12.16804389452603   -0.7339209249658375   
   19   12.72298804735438   -0.7339209249488197   
   20   13.27226831900744   -0.7339209249365428   
   21   13.81621476189632   -0.7339209249275397   
   22   14.35512379575268   -0.7339209249208374   
   23   14.8892629725969    -0.7339209249157863   
   24   15.41887489312131   -0.7339209249119263   
   25   15.94418045400206   -0.733920924908948   
   26   16.46538156214071   -0.7339209249066238   
   27   16.98266342011249   -0.7339209249047942   
   28   17.49619646365717   -0.7339209249033369   
   29   18.00613801451264   -0.7339209249021712   
   30   18.51263369862476   -0.7339209249012291   
   31   19.01581866962328   -0.733920924900462   
   32   19.51581866962328   -0.7339209248998368   
   33   20.0127509533112    -0.7339209248993227 

Answer 1

The Euler-Maclaurin formula gives the asymptotic expansion

\begin{equation} \sum_{k = 1}^{n} \frac{1}{k^{\sigma}} = \zeta(\sigma) + \sum_{k = 0}^{\infty} \frac{(-1)^k}{1-\sigma} \binom{1-\sigma}{k} B_k n^{1-\sigma-k}\,. \end{equation}

Thus $A = -B_1 = \frac{1}{2}$ and $B = -\frac{(-1)\sigma}{2}B_2 = \frac{\sigma}{12}$.

Taking a few more terms, we get

\begin{align} \zeta(\sigma) &= \sum_{k = 1}^n \frac{1}{k^{\sigma}} - \frac{n^{1-\sigma}}{1-\sigma} - \frac{1}{2n^{\sigma}} + \frac{\sigma}{12 n^{1+\sigma}} - \frac{\sigma(1+\sigma)(2+\sigma)}{720 n^{3+\sigma}} \\ &\qquad+ \frac{\sigma(1+\sigma)(2+\sigma)(3+\sigma)(4+\sigma)}{30240n^{5+\sigma}} + O(n^{-7-\sigma})\,. \end{align}

Answer 2

There is a standard technique that produces the complete asymptotic expansion for this sum and many others like it, which is to use harmonic sums and Mellin transforms.

Introduce the telescoping sum where $0\lt\sigma\lt 1$

$$S(x) = \sum_{k\ge 1} \left(\frac{1}{k^\sigma}- \frac{1}{(x+k)^\sigma}\right).$$

This sum has the property that

$$S(n) = \sum_{p=1}^n \frac{1}{p^\sigma},$$

so that $S(n)$ is the value we are looking for.

Re-write the sum as follows:

$$S(x) = \sum_{k\ge 1} \frac{1}{k^\sigma} \left(1-\frac{1}{(x/k+1)^\sigma}\right).$$

The sum term is harmonic and may be evaluated by inverting its Mellin transform.

Recall the harmonic sum identity $$\mathfrak{M}\left(\sum_{k\ge 1} \lambda_k g(\mu_k x);s\right) = \left(\sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} \right) g^*(s)$$ where $g^*(s)$ is the Mellin transform of $g(x).$

In the present case we have $$\lambda_k = \frac{1}{k^\sigma}, \quad \mu_k = \frac{1}{k} \quad \text{and} \quad g(x) = 1 - \frac{1}{(1+x)^\sigma}.$$

It follows that $$\sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} = \sum_{k\ge 1} \frac{1}{k^\sigma} \times k^s = \zeta(\sigma-s)$$ which has fundamental strip $\sigma-s > 1$ or $s < \sigma-1.$

We need the Mellin transform $g^*(s)$ of $g(x)$ which is $$\int_0^\infty \left(1 - \frac{1}{(1+x)^\sigma}\right) x^{s-1} dx$$

which is immediately seen to be a beta function integral with value $$g^*(s) = - \frac{1}{\Gamma(\sigma)} \Gamma(s)\Gamma(\sigma-s)$$

and fundamental strip $\langle -1, 0 \rangle.$ We check that the abscissa of convergence of the zeta function term is right in this strip as required. It follows that the Mellin transform $Q(s)$ of the harmonic sum $S(x)$ is given by

$$Q(s) = - \frac{1}{\Gamma(\sigma)} \Gamma(s)\Gamma(\sigma-s) \zeta(\sigma-s).$$

The Mellin inversion integral here is $$\frac{1}{2\pi i} \int_{\sigma-1-\varepsilon-i\infty} ^{\sigma-1-\varepsilon+i\infty} Q(s)/x^s ds$$

which we evaluate by shifting it to the right for an expansion at infinity.

First treat the pole from the zeta function term at $s=\sigma-1$, which has

$$\mathrm{Res}(Q(s)/x^s; s=\sigma-1) = -\frac{1}{\Gamma(\sigma)} \Gamma(\sigma-1)\Gamma(1) \times -1 \times x^{1-\sigma} = -\frac{1}{1-\sigma} x^{1-\sigma}.$$

For the pole at $s=0$ from the simple gamma function term we obtain

$$\mathrm{Res}(Q(s)/x^s; s=0) = -\frac{1}{\Gamma(\sigma)} \Gamma(\sigma) \zeta(\sigma) = -\zeta(\sigma).$$

For the pole at $s=\sigma$ from the compound gamma function term we obtain

$$\mathrm{Res}(Q(s)/x^s; s=\sigma) = -\frac{1}{\Gamma(\sigma)} \Gamma(\sigma) \times -1 \times\zeta(0) \times \frac{1}{x^\sigma} = -\frac{1}{2} \frac{1}{x^\sigma}.$$

The remaining poles are at $s = q+\sigma$ where $q\ge 1$ and contribute

$$\mathrm{Res}(Q(s)/x^s; s=q+\sigma) = -\frac{1}{\Gamma(\sigma)} \Gamma(\sigma+q) \frac{(-1)^{q+1}}{q!} \zeta(-q) \frac{1}{x^{q+\sigma}} \\ = - \prod_{p=0}^{q-1} (p+\sigma) \times \frac{(-1)^{q+1}}{q!} (-1)^q \frac{B_{q+1}}{q+1} \frac{1}{x^{q+\sigma}} = {q+\sigma-1\choose q} \frac{B_{q+1}}{q+1} \frac{1}{x^{q+\sigma}}.$$

The zero values of the Bernoulli numbers correctly represent cancelation of the gamma function poles by the trivial zeros of the zeta function.

Setting $x=n$ and observing that the shift to the right produces a minus sign we obtain the following asymptotic expansion:

$$S(n) = \sum_{p=1}^n \frac{1}{p^\sigma} \\ \sim \frac{1}{1-\sigma} n^{1-\sigma} + \zeta(\sigma) + \frac{1}{2} \frac{1}{n^\sigma} - \sum_{q\ge 1} {q+\sigma-1\choose q} \frac{B_{q+1}}{q+1} \frac{1}{n^{q+\sigma}}.$$

Actually computing the Bernoulli number terms we get for the example by OP with $\sigma=1/3$ the expansion

$$3/2\,{n}^{2/3}+\zeta \left( 1/3 \right) +1/2\,{\frac {1}{\sqrt [3]{n}}} -1/36\,{n}^{-4/3}+{\frac {7}{4860\,{n}^{10/3}}} \\-{\frac {13}{26244\,{n}^{16/3}}} +{\frac {247}{590490}{n}^{-{\frac {22}{3}}}} -{\frac {6175}{9565938}{n}^{-{\frac {28}{3}}}} \\+{\frac {406999}{258280326}{n}^{-{\frac {34}{3}}}} -{\frac {12966835}{2324522934}{n}^{-{\frac {40}{3}}}}+\cdots$$

This MSE link points to a series of similar calculations.

Answer 3

This is indeed true. In fact, this formula can be derived from the Euler summation formula with $f(x)=x^{-s}$ with $0<s<1$. We have

$$\begin{align*} \sum_{n\leq x}\frac{1}{x^s}&=\int_1^x\frac{dt}{t^s}-s\int\frac{t-[t]}{t^{s+1}}dt+1-\frac{x-[x]}{x^s} \\ &=\frac{x^{1-s}}{1-s}-\frac{1}{1-s}+1-s\int_1^\infty\frac{t-[t]}{t^{s+1}}dt+O(x^{-s}). \end{align*}$$

If we take the limit as $x\rightarrow\infty$ we find that

$$1-\frac{1}{1-s}-s\int_1^\infty\frac{t-[t]}{t^{s+1}}dt=\zeta(s)$$

so we then have

$$\lim_{x\rightarrow\infty}\left(\sum_{n\leq x}\frac{1}{n^s}-\frac{x^{1-s}}{1-s}\right)=\zeta(s),\;\;0<s<1$$

as desired.

Note that $[t]$ is the greatest integer function. This proof can be found in Introduction to Analytic Number Theory by Apostol.