Producing two functions from a rotated parabola that graph the parabola in question

Question

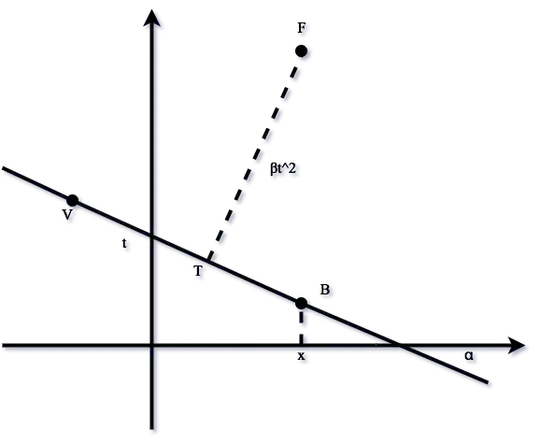
The following is my attempt at splitting a rotated parabola into two real functions of one real variable (the $x$-coordinate). Let $P$ be the parabola, $V = (x_V, y_V)$ the vertex of $P$, $\alpha$ the angle between the $x$-axis and the line perpendicular to the axis of symmetry of $P$ and growing in counter-clockwise direction. Finally, let $g(t) = \beta t^2$ define the "geometry" of $P$.

Now, the line perpendicular to the axis of symmetry of $P$ and passing through $V$ (call it $\ell$) is given by equation

$$ y = (x - x_V) \tan \alpha + y_V. $$

Let $x$ be given. We wish to calculate two values $y_1$ and $y_2$ such that $(x, y_1)$ and $(x, y_2)$ are located at the parabola's "lower" and "upper" parts. To do that, I start from $(x, 0)$, go up or down until I reach $\ell$ at point $B$, travel through the line segment $BT$, and finally travel through $TF$. If we fix $V$, $T$ becomes

$$ T(t) = (x_V + t \cos \alpha - \beta t^2 \sin \alpha, y_V + t \sin \alpha + \beta t^2 \cos \alpha). $$

Next, we set $x = x_V + t \cos\alpha - \beta t^2 \sin \alpha$ and solve for $t$ $$ -\beta \sin(\alpha)t^2 + \cos(\alpha)t + (x_V - x) = 0, $$

which has solutions $$ \begin{aligned} t &= \frac{-\cos\alpha \pm \sqrt{\cos^2\alpha - 4(-\beta\sin\alpha)(x_V - x)}}{-2\beta\sin\alpha} \\ &= \frac{\cos\alpha \pm \sqrt{\cos^2\alpha + 4\beta\sin\alpha(x_V - x)}}{2\beta\sin\alpha}. \end{aligned} $$ Next, we need to find out $|VB|$: $$ \begin{aligned} |VB| &= \sqrt{(x - x_V)^2 + (\tan(\alpha)x - \tan(\alpha)x_V + y_V - y_V)^2} \\ &= \sqrt{(x - x_V)^2 + (\tan(\alpha)x - \tan(\alpha)x_V)^2} \\ &= \sqrt{(x - x_V)^2 + \tan^2(\alpha)(x - x_V)^2} \\ &= \sqrt{(x - x_V)^2 (1 + \tan^2(\alpha))^2} \\ &= (x - x_V)\sqrt{1 + \tan^2 \alpha}. \end{aligned} $$ Finally, the desired $y_1$ or $y_2$ are given by $$ \begin{aligned} y &= y_S + \sqrt{(|VB| - t)^2 + (\beta t^2)^2} \\ &= y_S + \sqrt{(|VB| - t)^2 + \beta^2 t^4}, \end{aligned} $$ where $y_S = \tan(\alpha)(x - x_V) + y_V$.

Question: is this calculation correct? Does it work for all $\alpha$, $\beta$, $V$? (Except $\alpha = n\pi$.)

Answer 1

The form of the solution will depend on the form in which you put the parabola. Any parabola (or circle or ellipse or hyperbola) in the plane can be expressed in the form $By^2 + Ax^2 + Cx + Dy + Exy + F = 0$. In the case of parabolas of interest here, that do not open up or down, $B$ will not be zero, so without loss of generality we can divide out by $B$ and assume the parabola is of the form $y^2 + Ax^2 + Cx + Dy + Exy + F = 0$. The problem is relatively easy to solve in this form. First, separate all terms with a $y$:

$y^2 + (Ex + D)y = -Ax^2 - Cx - F.$

Then complete the square in $y$ on the LHS:

$y^2 + (Ex + D)y + (\frac{Ex+D}{2})^2 = (\frac{E^2}{4} -A)x^2 + (\frac{ED}{2} - C)x + (\frac{D^2}{4} - F)$

That is,

$(y + \frac{Ex+D}{2})^2 = (\frac{E^2}{4} -A)x^2 + (\frac{ED}{2} - C)x + (\frac{D^2}{4} - F)$

so that

$ y + \frac{Ex+D}{2} = \pm\sqrt{(\frac{E^2}{4} -A)x^2 + (\frac{ED}{2} - C)x + (\frac{D^2}{4} - F)}$

or

$ y = -\frac{Ex+D}{2} \pm\sqrt{(\frac{E^2}{4} -A)x^2 + (\frac{ED}{2} - C)x + (\frac{D^2}{4} - F)}$

with the "upper" curve for $y$ being given by the choice of + in the $\pm$ and the lower by -. (Aside: and there is no solution when the expression inside the square root is negative. If $E^2 < 4A$, that clearly happens whenever $x$ is sufficiently negative or sufficiently positive. On the other hand, we know a rotated parabola either "opens to the right" or "opens to the left", so there will at least be two solutions for all sufficiently positive or all sufficiently negative $x$. Hence, we conclude that if the original curve was a parabola, then in fact $E^2 \geq 4A$.)

Anyhow, to use this solution in your case, I suggest you convert your parabola into this form. In particular, you can start with the upward-opening parabola with vertex $(a, b)$ which has equation $u - b = \beta(v-a)^2$ and then simply rotate about the origin by an angle $\alpha$, e.g. by substituting $u = x\cos\alpha - y\sin\alpha$ and $v = x\sin\alpha + y\cos\alpha$. You can arrange that the rotated vertex ends up at $(x_V, y_V)$ by taking $a = x_V\cos\alpha - y_V\sin\alpha$ and $b = x_V\sin\alpha + y_V\cos\alpha$.

I recognize that this is not a direct answer to the question of whether the expressions you list are correct, but I hope it will still be helpful, given that the original question of what are the expressions for the "upper and lower branches" of the rotated parabola is much simpler starting from the general quadratic equation in the plane as expressed in this solution.