This question is motivated by my partial answer to a different question. I will use $\mathbb R_+$ to denote the set of nonnegative reals.
Consider the standard simplex $\Delta^n=\{(x_0,\dots,x_n)\in\mathbb R_+^{n+1}:x_0+\dots+x_n=1\}.$ We are given a continuous function $f:\Delta^n\to\mathbb R_+^{n+1}$ with the property that it preserves zero coordinates, that is, if $x_i=0$ then $f(x)_i=0.$ Thus vertices of the simplex map to points on the coordinate axes, $1$-faces (edges) map to curves on the coordinate $2$-planes, and so on. I believe the following conjecture is true, but I don't know how to prove it for arbitrary $n$:
Conjecture: For any $y\in\mathbb R_+^{n+1}$, there exists a point $x\in\Delta^n$ such that $f(x)=ay$ for some scalar $a\in\mathbb R_+$. Geometrically, every ray from the origin lying in $\mathbb R_+^{n+1}$ must intersect the surface $S = f(\Delta^n)$.
Here are some examples with $n=1,y=(1,1)$ and $n=2,y=(1,1,1)$ respectively:
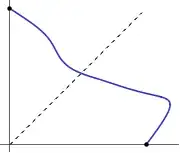
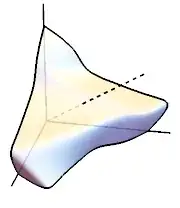
These examples suggest that when $y\in\operatorname{int}\mathbb R_+^{n+1}$, the boundary $\partial S=f(\partial\Delta^n)$ "surrounds" the line $\{ay:a\in\mathbb R\}$, so the surface $S$ must intersect the line. Thus I feel the conjecture is essentially topological in nature and should have a natural proof based on something like homotopy theory. Unfortunately, I don't know any homotopy theory.
![[1]: https://i.stack.imgur.com/WZ](../../images/b949df35ea504ce6f116c06fc9bc0757.webp)