Can every curve be subdivided equichordally?

Question

This question build on top of this other question: Dividing a curve into chords of equal length, for which I wrote an (incomplete) answer. I got the feeling we might need some help from a real topologist. Let me repeat the crucial definitions. We are dealing with curves $c:[0,1]\to\Bbb R^m$ which are assumed to be continuous maps.

Definition. Given a curve $c:[a,b]\to\Bbb R^m$ and $n\in\Bbb N$, an equichordal subdivision of $c$ into $n$ segments is a sequence $t_i,i=0,...,n$ with $$a=t_0\leq t_1\leq\cdots\leq t_{n-1}\leq t_n=b, \qquad \|c(t_{i-1})-c(t_i)\|=\Delta,\quad \text{for all $i=1,...,n$}$$ and some chord length $\Delta$.

Essentially this means we are looking for $n+1$ points on a curve (including the end points) so that neighboring points all have the same Euclidean distance $\Delta$ from each other. Now the big question is:

Question: Is it always possible for arbitrary curves $c$ and $n\in\Bbb N$ to equichordally subdivide $c$ into $n$ segments?

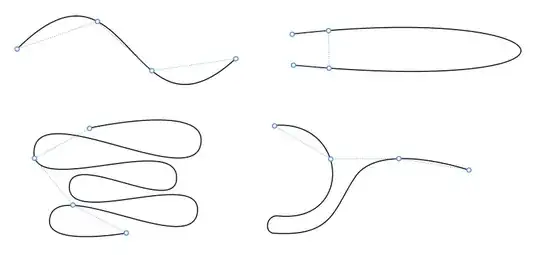
It seems not so strange to assume that this might be. However, look at the following examples for $n=3$. The subdivision might not at all follow the shape of the curve or will look similar to a subdivision with equal arc lengths (for small $n$). Most of the time, for a given $n$ the final chord length $\Delta$ is pretty unpredictable.

Further information for the interested reader:

• In one of my answers I gave a proof that felt good at first, but I cited a result incompletely. I used this statement despite some answer below gave a nice counter-example. Currently I have no idea how to justify that this is no problem. I also think that my proof might be too complicated, even though it proves a more general statement (the existence of a continuous transition from a trivial subdivision to a subdivision of the whole curve).
• In this answer Rahul gave a proof for the cases $n=2$ and $n=3$. He (and now me too) got the feeling that this might be generalizable by someone with enough experience in topology (homotopy maybe?). I really prefer Rahul's approach for its simplicity. He even posted a follow up question on it over here.
• As far as I know, there is no easy way to find such a subdivision. For sufficiently well behaved curves it might be possible to just choose some reasonable subdivision and wiggling the points a bit to bring them into the right spot for equichordality. However, this will fail in general. Also, given an equichordal subdivision of some subcurve of $c$, it is highly non-trivial to "stretch" it out to cover the whole curve while still keeping the desired property. I found counterexamples for most easy approaches. For example, test your procedure on the examples given above.
• I have not studied any possible counter-examples in higher dimensions. I only looked at plane curves so far. I have no clue what might hide over there.

Answer 1

Niels Diepeveen helped me fill the gap in my incomplete proof, which I've deleted from the original question and moved here because it fits this question better.

---

We take the curve to be $c:[0,1]\to\mathbb R^m$ and assume that $c(0)\ne c(1)$ (otherwise a trivial solution exists). A subdivision into $n$ segments is determined by its vector of interval lengths, $s=(s_1,\dots,s_n)$ where $s_i=t_i-t_{i-1}$. The set of all valid $s$ forms the standard simplex $$\Delta^{n-1}=\left\{(s_1,\dots,s_n):\sum_{i=1}^n s_i=1, s_i\ge 0\text{ for all }i=1,\dots,n\right\},$$ which is an $(n-1)$-dimensional polytope embedded in $\mathbb R^n$. In fact, $\Delta^{n-1}$ lies in the nonnegative orthant $\mathbb R_+^n$ and its boundary lies in $\partial\mathbb R_+^n$: vertices lie on the coordinate axes, $1$-faces (edges) lie on the coordinate $2$-planes, and so on.

Consider the function $d:\Delta^{n-1}\to\mathbb R_+^n$ mapping the vector of interval lengths to the vector of chord lengths, $$d(s)=(\|c(t_1)-c(t_0)\|,\dots,\|c(t_n)-c(t_{n-1})\|),$$ where $t_i=\sum_{j=1}^i s_j$. This function is nonnegative ($d(s)_i\ge 0$), nondegenerate ($d(s)\ne0$ because $c(t_0)\ne c(t_n)$), and preserves zero coordinates ($d(s)_i=0$ if $s_i=0$). Zero coordinate preservation is the key property here: it means that while $d$ may transform $\Delta^{n-1}$ into an arbitrarily complicated, possibly self-intersecting $(n-1)$-dimensional surface, it cannot detach its boundary from the faces of $\partial\mathbb R_+^n$. Vertices still lie on the coordinate axes, edges become curves lying on the coordinate $2$-planes, and so on.

We want to prove that there exists an $s\in\Delta^{n-1}$ such that all the components of $d(s)$ are equal. Equivalently, we want to show that the surface $d(\Delta^{n-1})$ intersects the line $\{(a,\dots,a):a\in\mathbb R\}$.

From left to right: A curve $c([0,1])$, the corresponding deformed simplex $d(\Delta^{n-1})$ for $n=2$, $d(\Delta^{n-1})$ for $n=3$.

Rescaling $d(s)$ so that its components sum to $1$, we obtain the map $$\hat d(s) = \frac{d(s)}{\sum_{i=1}^n d(s)_i},$$ which is well-defined and continuous because $d(s)$ is never zero. It is easy to verify that $\hat d$ maps the simplex $\Delta^{n-1}$ to itself; further, zero coordinate preservation implies that $\hat d$ also maps each face of $\Delta^{n-1}$ to itself. It can be shown using Brouwer's fixed point theorem that such a mapping must be surjective. Therefore, there exists an $s\in\Delta^{n-1}$ such that $\hat d(s)=(\frac1n,\dots,\frac1n)\in\Delta^{n-1}$, which is equivalent to the desired result.

In fact, we have proved a slightly stronger property: For any vector of nonnegative chord length ratios $r=(r_1,\dots,r_n)$, we can find a subdivision $s$ such that $d(s)=ar$ for some $a\in\mathbb R$.

Answer 2

Here's an alternative approach that could work generally. One may be able to reason by induction on $n$ using a connectedness argument. One would need to establish connectedness of a certain level set, but this might be hard.

---

The proposition is quite obvious for $n=1$. Suppose we know the proposition to hold for $n\geq 1$, that is, suppose we know that for any (continuous, simple) curve $\gamma:[0,1]\to\Bbb R^d$ (I'll take $d=2$) there exist $0\leq t_1\leq\cdots\leq t_n\leq1$ such that, if we set $t_0=0$ and $t_{n+1}=1$, $$\forall k\in\lbrace 1,\dots,n\rbrace,\quad\|\gamma(t_{k+1})-\gamma(t_{k})\|=\|\gamma(t_{k})-\gamma(t_{k-1})\|$$ Note that since $\gamma(0)\neq\gamma(1)$ by non intersection, the $t_i$ must actually all be different, so that in actuality one has $0<t_1<\cdots< t_n<1$.

Now let $c:[0,1]\to\Bbb R^d$ be a (continuous, simple) curve. We shall write vectors $x\in\Bbb R^{m}$ as $x_\bullet=(x_1,\dots,x_m)$ et us define $$T_{n+1}=\lbrace t_\bullet\in\Bbb R^{n+1}\mid 0\leq t_1\leq\cdots\leq t_n\leq t_{n+1}\leq1\rbrace$$ (again, we write $t_0=0$ and $t_{n+2}=1$) and set, for $\theta\in[0,1]$, $$T_{n+1}^\theta=\lbrace t_\bullet\in T_{n+1}\mid t_{n+1}=\theta\rbrace\simeq\begin{cases}* & \text{if }\theta=0\\[3mm]\theta\cdot T_n & \text{if }\theta>0 \end{cases}$$ Let us consider the function $\varphi:T_{n+1}\to\Bbb R_+$ defined by the formula $$\varphi(t_\bullet)=\sum_{k=1}^{n}\Big[\|c(t_{k+1})-c(t_{k})\|^2-\|c(t_{k})-c(t_{k-1})\|^2\Big]^2$$ Note that the sum only goes to $t_{n+1}$. Let us set $Z=\varphi^{-1}(0)$. This is the set of all equichordal subdivisions that start at $c(0)$, but may end before $c(1)$, that is, we drop the requirement that the last chord from $c(t_{n+1}$ to $c(1)$ have the same length as the other chords.

What can we say about $Z$ ?

1. $Z$ is a closed subset of $T_{n+1}$,
2. for every $\theta\in[0,1]$, the set $Z\cap T_{n+1}^\theta$ is non empty,
3. actually, for every $\theta\in(0,1]$, the set $Z\cap T_{n+1}^\theta$ is included in the interior of $T_{n+1}^\theta$ (where all inequalities are strict).

The second point follows from induction : for every $\theta\in[0,1]$, the (continuous, simple if $\theta>0$, constant if $\theta=0$) curve $$c^\theta:[0,1]\to\Bbb R^d,\;t\mapsto c(\theta t)$$ has an equichordal subdivision with $n$ nodes.

Question. Is $Z$ connected ?

Suppose it were, then consider the functions $\Delta^L,\Delta^R:T_{n+1}\to\Bbb R_+$ defined by $$\Delta^L(t_\bullet)=\|c(t_1)-c(0)\|^2,\quad \Delta^R(t_\bullet)=\|c(1)-c(t_{n+1})\|^2$$ Then at the point $t^0_\bullet=(0,0,\dots,0)\in Z$, $$\Delta^L(t_\bullet^0)=0\quad\text{and}\quad\Delta^R(t_\bullet^0)=\|c(1)-c(0)\|^2>0$$ while for every $t_\bullet^1\in Z\cap T_{n+1}^1\;(\neq\emptyset)$, $$\Delta^L(t_\bullet^1)>0\quad\text{and}\quad\Delta^R(t_\bullet^1)=\|c(1)-c(1)\|^2=0$$

Thus, the continuous function $$\Delta^L-\Delta^R$$ switches sign on $Z$. If $Z$ were connected, then there would exist a point where the two functions coïncide, and such a point is exactly an equichordal subdivision.

---

Here are a few illustrations of this in the case $n=1$ (i.e. $n+1=2$). Consider the curve $c$ drawn in the plane as follows: The following represents $Z$ in this particular case : there can be either one, two or three equichordal subdivisions of $c$ with prescribed endpoint and one node, and this is how these possibilities are distributed :

The triangle represents $T_2$ in the plane, the horizontal lines are the $T_2^\theta$ for four values of $0<\theta<\theta'<1$. One sees in this example that the level set $Z$ is path connected. It even looks like a manifold ($c$ is rather smooth).

Answer 3

An initial point for collecting ideas:

Let us assume that $\gamma:[0,1]\mapsto\mathbb{R}^2$ is an injective $C^2$ function. In such a case it is a rectifiable curve and there is an arc length parametrization such that $\gamma:[0,L]\mapsto\mathbb{R}^2$ still is a $C^2$ function and $$ \forall \ell\in[0,L],\qquad \int_{0}^{\ell}\left\|\dot\gamma(t)\right\|\,dt = \ell.$$ We may further assume $\gamma(0)=(0,0)$ without loss of generality and get that $$ \forall \ell\in[0,L],\qquad \ell=\int_{0}^{\ell}\left\|\dot\gamma(t)\right\|\,dt\geq \left\|\gamma(\ell)\right\| $$ from the triangle inequality. If we consider the points $$ P_0=\gamma(0),\quad P_1=\gamma\left(\frac{L}{n}\right),\quad P_2=\gamma\left(\frac{2L}{n}\right),\quad \ldots $$ all the chords between consecutive points have a length that is positive (by injectivity and the $C^2$ constraint) and bounded above by $\frac{L}{n}$. Let $c_1,c_2,\ldots,c_n$ the sequence of those lengths. Without moving $P_0$ or $P_n$, we may move $P_1$ along the $P_0 P_2$ arc in $\gamma$ in such a way that $c_1=c_2$: it is enough to intersect $\gamma$ with the perpendicular bisector of the $P_0 P_2$ segment. If multiple choices are possible, we may take the new $P_1$ point that is closer to the old $P_1$ point. Then we may move $P_2$ along the $P_1 P_3$ arc and so on. After we move $P_{n-1}$ we restart in the opposite direction by moving $P_{n-2}, P_{n-3},\ldots, P_1$, then again $P_2,P_3,\ldots,P_{n-1}$. If the variance of the set of lengths $\{c_1,\ldots,c_n\}$ decreases at each step, the condition $\gamma\in C^2$ ensures that $\gamma$ cannot behave too bad, hence this process is expected to converge to an equichordal distribution.

---

The following approach appears to be much more effective: let us assume that $\gamma:[0,L]\to\mathbb{R}^2$ is an injective $C^1$ curve with an arc-length parametrization. For some $r>0$, let $A(r)$ be the farthest point from $P_0=\gamma(0)$, with respect to the arc length, such that there is a $n$-equichordal distribution over the $P_0 A(r)$ arc with chords having length $r$. Similarly, let $B(r)$ the farthest point from $\gamma(L)$, with respect to the arc length, such that the chord joining $\gamma(L)$ and $B(r)$ has length $r$. Let us consider the intervals $J_0=[0,\gamma^{-1}A(r)]$ and $J_1=[\gamma^{-1}B(r),L]$. For small values of $r$ they are clearly disjoint, since the total length of consecutive chords cannot exceed the length of the curve considered. For large values of $r$ they are clearly overlapping, since by inductive hypothesis there is a $n$-equichordal distribution for the curve restricted to the interval $[0,L-\varepsilon]$. If continuity holds (unluckily, it is not always so: it is enough to consider curves with a very small radius of curvature somewhere) it follows that for some value of $r$ we have $A(r)=B(r)$, hence it is possible to join a $n$-equichordal distribution for the $P_0 A(r)$ arc with a chord $B(r)\gamma(L)$ having the same length of the previous ones. That leads to a $(n+1)$-equichordal distribution for $\gamma$.

This is not constructive at all but the approach let us make enough room for another chord should prove the claim nicely, once the lack of continuity issue is fixed.

Answer 4

This is too long for a comment, it's not a complete solution, only a sketch of solution ...

---

I think it shouldn't be too hard to prove the following :

Lemma. Let $c$ be some $C^1$ curve parametrized by arc length. There exists some $N\gg 0$ such that for all $n\geq N$ equichordal subdivisions in $n$ steps exist. Furthermore, there is a canonical one.

The idea would be that by uniform continuity of $\dot{c}$ on $[a,b]$, there exists $\delta>0$ such that on each segment $[x,x+\delta]$ of $[a,b]$, the curve deviates very little from the chord (i.e. straight line) that links $c(x)$ and $c(x+\delta)$.

So for instance, for any $0\ll k<1$ very close to $1$, there will exist $\delta>0$ such that for all $a\leq x\leq y\leq b$,

$$|y-x|\leq\delta\implies k\cdot|y-x|\leq \|c(y)-c(x)\|\leq |y-x|$$

Let $k$ be very close to $1$, and $\Delta\leq k\cdot \delta$. On every such segment $[x,x+\delta]\subset[a,b]$, there should be exactly one other point $y=y_x(\Delta)\in[x,x+\delta]$ such that $$\|c(x)-c(y)\|=\Delta,$$ futhermore $y_x(\Delta)$ depending continuously on $x$ and $\Delta$. One would then consider, for any imposed chord length $0<\Delta\leq k\delta$, the sequence of times in $[a,b]$ constructed like so : $x_0(\Delta)=a$, $x_{k+1}(\Delta)=y_{x_k(\Delta)}(\Delta)$ : eventually (in terms explicitely quantifiable in terms of arc length and $\Delta$), this sequence would not make sense anymore (because one runs out of curve to travel along), one then sets $x_{k+1}=b$. Call $k_\Delta$ the first $k$ for which $x_k(\Delta)=b$.

The point is that the functions $(]0,k\cdot \delta]\ni)\Delta\mapsto x_k(\Delta)$ will be continuous, weakly increasing, and will satisfy $$a=x_0(\Delta)< x_1(\Delta)< x_2(\Delta)<\cdots< x_{k_\Delta}(\Delta)=x_{k_\Delta+1}(\Delta)=\cdots=b$$ with for every $k$, $\lim_{\Delta\to 0}x_k(\Delta)=a$ and for $k$ big enough, $x_{k}$ constant equal to $b$ for $\Delta$ near $k\cdot\delta$.

Now take $n\gg\frac1\delta$ : There will be a smallest $\Delta_n$ such that $x_n\equiv b$ on $[\Delta_n,k\cdot\delta]$ : this $\Delta_n$ will be the chord distance in an equichordal subdivition of $c$ of length $n$ with time subdivision $$a=x_0(\Delta_n)< x_1(\Delta_n) < x_2(\Delta_n)<\cdots< x_{n}(\Delta_n)=b$$