I suspect there are a number of errors in the equations, but it's unclear
because the entire idea behind all these transformations of coordinates is unclear.
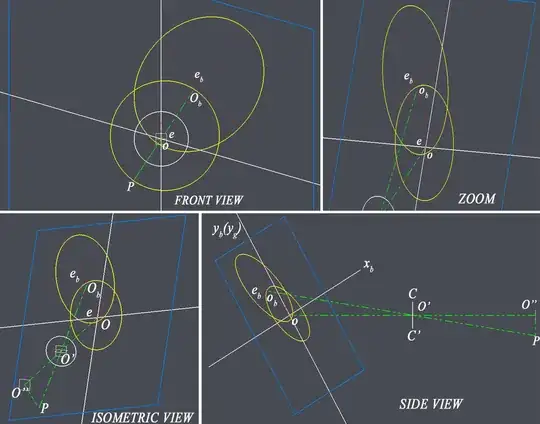
Yes, the ellipse projected onto an oblique plane can be rotated and translated in 3-D space back onto a plane parallel to the circle. But what's the purpose of that? Or you could rotate and translate some ellipse in the parallel plane onto the projected ellipse, but how do you construct the correct ellipse in the parallel plane to begin with?
It seems to me a much simpler approach is to write out the equations of the cone and the plane in three dimensions ($x,$ $y,$ and $z$ coordinates)
and solve the equations.
If the circle is parallel to the $x,y$ plane of the first set of coordinates, it may be easiest to write the equations first in that system and then transform the coordinates (all three coordinates, not just $x$ and $y$)
before solving the equations.
Here's an attempt via the second approach.
I make a few assumptions based on an interpretation of the diagrams
of the cone and the intersecting plane.
Assume the coordinates of the point $O$ in all three coordinate systems are
$(x^r_O,y^r_O,z^r_O) = (x^g_O,y^g_O,z^g_O) = (x^b_O,y^b_O,z^b_O) = (0,0,0).$
Assume the coordinates of $O'$ in the "red" system are
$(x^r_{O'},y^r_{O'},z^r_{O'}) = (0,0,z^r_{O'}).$
Assume the circle $CC'$ has radius $R$ and is parallel to the red plane,
so the "red" coordinates of points on that circle satisfy the
simultaneous equations
\begin{align}
(x^r)^2 + (y^r)^2 &= R^2,\\ z^r &= z^r_{O'}.
\end{align}
Now to find an equation of the cone whose vertex is at $P$ and whose sides
pass through the circle $CC',$
consider an arbitrary cross-section of the cone parallel to the red plane.
The cross-section is a circle with center on the line $PO'$ and radius proportional to the distance from the parallel plane through $P.$
In particular, the center of the cross-section has "red" coordinates
$(x^r,y^r,z^r) = \left(h(z^r - z^r_{O'}), k(z^r - z^r_{O'}), z^r \right)$
where $$h = \frac{x^r_P}{z^r_P - z^r_{O'}} \quad\text{and}\quad
k = \frac{y^r_P}{z^r_P - z^r_{O'}},$$
and the radius is
$\left\lvert\dfrac{z^r_P - z^r}{z^r_P - z^r_{O'}}\right\rvert R.$
The equation of the cone in "red" coordinates is therefore
$$
\left(x^r - h(z^r - z^r_{O'})\right)^2
+ \left(y^r - k(z^r - z^r_{O'})\right)^2
= \left(\frac{z^r_P - z^r}{z^r_P - z^r_{O'}} R\right)^2. \tag1
$$
Now to find the equation in "blue" coordinates, we need to work out the conversion of coordinates.
The point with "blue" coordinates $(x^b,y^b,z^b)_b$ has "green" coordinates
$$(x^g,y^g,z^g)_g =
(x^b\cos\beta + z^b\sin\beta, y^b, -x^b\sin\beta + z^b\cos\beta)_g.$$
(This assumes that a small positive rotation angle $\beta$ would bring the positive $z$ axis of the blue plane closer to the positive $x$ axis of the green plane; if the positive direction of rotation is in the other direction, just reverse the sign of $\sin\beta$ in the formula.)
The point with "green" coordinates $(x^g,y^g,z^g)_g$ has "red" coordinates
$$(x^r,y^r,z^r)_r =
(x^g, y^g\cos\alpha - z^g\sin\alpha, y^g\sin\alpha + z^g\cos\alpha)_r$$
(assuming the positive direction of rotation takes the positive $y$ axis toward the positive $z$ axis; if it goes the other way, reverse the sign of $\sin\alpha$).
Now suppose a point on the cone has "blue" coordinates $(x^b,y^b,z^b)_b.$
The "red" coordinates of that point, $(x^r,y^r,z^r)_r,$ have the formulas
\begin{align}
x^r &= x^g = x^b\cos\beta + z^b\sin\beta,\\[6pt]
y^r &= y^g\cos\alpha - z^g\sin\alpha \\
&= y^b\cos\alpha - (-x^b\sin\beta + z^b\cos\beta)\sin\alpha \\
&= x^b\sin\beta\sin\alpha + y^b\cos\alpha - z^b\cos\beta\sin\alpha,\\[6pt]
z^r &= y^g\sin\alpha + z^g\cos\alpha \\
&= y^b\sin\alpha + (-x^b\sin\beta + z^b\cos\beta)\cos\alpha \\
&= - x^b\sin\beta\cos\alpha + y^b\sin\alpha + z^b\cos\beta\cos\alpha.
\end{align}
That is, the "red" coordinates of the point with "blue" coordinates $(x^b,y^b,z^b)_b$ are
\begin{align}
x^r &= a_{11}x^b + a_{13}z^b, \tag2\\
y^r &= a_{21}x^b + a_{22}y^b + a_{23}z^b, \tag3\\
z^r &= a_{31}x^b + a_{32}y^b + a_{33}z^b \tag4
\end{align}
where
\begin{align}
a_{11} &= \cos\beta, & & & a_{13} &= \sin\beta, \\
a_{21} &= \sin\beta\sin\alpha, & a_{22} &= \cos\alpha, & a_{23} &= -\cos\beta\sin\alpha,\\
a_{31} &= -\sin\beta\cos\alpha, & a_{32} &= \sin\alpha, & a_{33} &= \cos\beta\cos\alpha.
\end{align}
If $(x^b,y^b,z^b)_b$ are the "blue" coordinates of a point on the cone, then the "red" coordinates of the same point must satisfy Equation $(1),$ above. That is, we can use Equations $(2),$ $(3),$ and $(4)$ to make substitutions for $x^r,$ $y^r,$ and $z^r$ in Equation $(1).$
The resulting equation is
\begin{multline}
\left(a_{11}x^b + a_{13}z^b
- h(a_{31}x^b + a_{32}y^b + a_{33}z^b - z^r_{O'})\right)^2 \\
+ \left(a_{21}x^b + a_{22}y^b + a_{23}z^b
- k(a_{31}x^b + a_{32}y^b + a_{33}z^b - z^r_{O'})\right)^2 \\
= \left(\frac{z^r_P - (a_{31}x^b + a_{32}y^b + a_{33}z^b)}
{z^r_P - z^r_{O'}} R\right)^2. \tag5
\end{multline}
But we are only interested in the intersection of the cone with the blue plane, where $z^b = 0.$
So we can substitute $z^b = 0$ in Equation $(5),$ with the result
\begin{multline}
\left(a_{11}x^b - h(a_{31}x^b + a_{32}y^b - z^r_{O'})\right)^2
+ \left(a_{21}x^b + a_{22}y^b - k(a_{31}x^b + a_{32}y^b - z^r_{O'})\right)^2 \\
= \left(\frac{z^r_P - (a_{31}x^b + a_{32}y^b)}
{z^r_P - z^r_{O'}} R\right)^2.
\end{multline}
Now, this may still look daunting, but everything in this equation except $x^b$ and $y^b$ is a known constant. You can multiply out the products and squares of the expressions in parentheses until everything is just individual terms, each of which is some kind of constant times
$x^b,$ $y^b,$ $(x^b)^2,$ $(y^b)^2,$ or $x^b y^b.$
Collect all the terms together on one side of the equation so that it looks like
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 ,$$
and then you can find the center, major axis, minor axis, and angle of the ellipse by following one of the procedures in the answers to
these questions:
Note that the center of the ellipse will not usually be at the same
point as the projection of $O'$ onto the blue plane.