Following the discussion in the comments, here is a proposal assuming that angles $\alpha$ and $\beta$ are known.
Notations
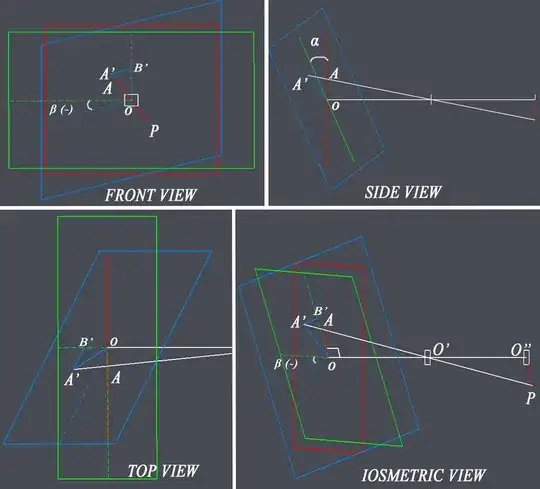
I'll take the red plane/coordinates as reference, and take $O$ as everyone's origin.
For any point $M$, I'll denote its coordinates by $(x_M^r,y_M^r,z_M^r)^r$ when in the red coordinate system, $(x_M^b,y_M^b,z_M^b)^b$ when in the blue coordinate system and $(x_M^g,y_M^g,z_m^g)^g$ if in the green system.
From the isometric view, I'll assume the $X$ axis points to the right, $Y$ upwards, and $Z$ also to the right.
Then for $O'$ its coordinates (red) are $(0,0,OO')^r$;
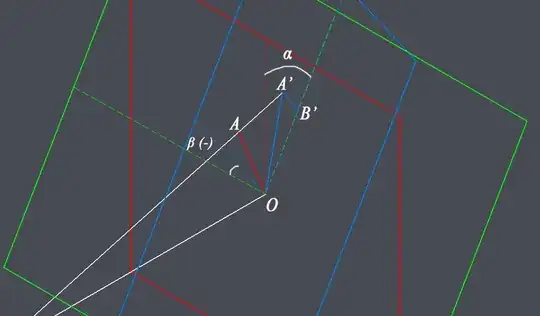
$A'$ is $(A'B',B'O,0)^b$.
Using Pythagoras we know that $B'O^2=A'O^2-A'B'^2$.
Strategy for getting $AO$
Now notice that $A$ is the intersection between the line $O'A'$ and the red plane of equation $z^r=0$. One way to solve this is to obtain the parametric equation of line $(A'O')$ in the red system, then find out which point of this line satisfies $z^r=0$. We then obtain the coordinates of $A$ in the red system and can then compute the distance $AO=\sqrt{(x^r_A)^2+(y^r_A)^2}$.
So first up we need the coordinates of $A'$ in the red system (by using angles $\alpha$ and $\beta$).
Coordinate change
In general for any point $M$
\begin{align*}
x^g_M &= x^r_M \\
y^g_M &= y_M^r\cos\alpha +z_M^r\sin\alpha \\
z_M^g &= -y_M^r\sin\alpha +z_M^r\cos\alpha
\end{align*}
These equations are compatible with your figures if $\alpha<0$, otherwise change the sign.
\begin{align*}
y^b_M &= y^g_M \\
z^b_M &= z_M^g\cos\beta+x_M^g\sin\beta\\
x_M^b &= -z_M^g\sin\beta+x_M^g\cos\beta
\end{align*}
Again these equations work with your figures if $\beta<0$. (Algebraic vs geometric is always fun.)
In particular you have
\begin{align*}
x^r_M &= z^b_M\sin\beta + x^b_M\cos\beta \\
y^r_M &= y^b_M\cos\alpha -\left( z^b_M\cos\beta -x^b_M\sin\beta \right)\sin\alpha \\
z^r_M &= y^b_M\sin\alpha +\left( z^b_M\cos\beta -x^b_M\sin\beta \right)\cos\alpha
\end{align*}
So in particular (bis) for $A'$
\begin{align*}
x^r_{A'} &= A'B'\cos\beta &(1)\\
y^r_{A'} &= B'O\cos\alpha +A'B'\sin\beta\sin\alpha &(2)\\
z^r_{A'} &= B'O\sin\alpha -A'B'\sin\beta\cos\alpha &(3)
\end{align*}
The line $(A'O')$
$$
\text{line }(A'O')=
\left\{ \Big( x^r(t),\ y^r(t),\ z^r(t) \Big)^r \mid t\in\mathbb R\right\}
$$
where
\begin{align*}
x^r(t) &= tx^r_{A'} +(1-t)x^r_{O'} & (4)\\
y^r(t) &= ty^r_{A'} +(1-t)y^r_{O'} & (5) \\
z^r(t) &= tz^r_{A'} +(1-t)z^r_{O'}
\end{align*}
In particular we have $z^r(t)=0 \iff t=-\frac{ z^r_{O'} }{z^r_{A'}-z^r_{O'}} \quad (6)$
Now if you inject equation $(6)$ into $(4)$ and $(5)$, you obtain $x^r_A$ and $y^r_A$ which suffice to conclude.
Edit
Corrected a few typos on equation numbers.