Finding the angle of rotation of an ellipse from its general equation and the other way around

Question

The general equation for an ellipse is $Ax^2+Bxy+Cy^2+D=0$. How do I find the angle of rotation, the dimensions, and the coordinates of the center of the ellipse from the general equation and vice versa? Please avoid using matrices or parametric equations. I'd like all-in-one equations for each parameter.

Answer 1

The general equation of an ellipse is: $$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$ if: $$4AC - B^2 > 0$$ The trick is to eliminate B so that the xy term vanishes.
If $B<>0$ then the ellipse is rotated and the angle of rotation is obtained from: $$tan(2 \theta) = \frac {B}{A-C}$$ $0 < \theta < \frac {\pi}{4}$

$$\cos {\theta} = \sqrt{\frac{1 + \cos{2 \theta}}{2}}$$ $$\sin{\theta} = \sqrt{\frac{1 - cos{2 \theta}}{2}}$$ Determine the new equation of the ellipse by calculating the following coefficients:
$A' = A \cos^2{\theta} + B \cos{\theta} \sin{\theta} + C \sin^2{\theta}$
$B' = 0$
$C' = A \sin^2{\theta} - B \cos{\theta} \sin{\theta} + C \cos^2{\theta}$
$D' = D \cos{\theta} + E \sin{\theta}$
$E' = -D \sin{\theta} + E \cos{\theta}$
$F' = F$

The resulting equation: $A'x'^2 + C'y'^2 + D'x' + E'y' + F' = 0$
After writing this equation in the form: $$ \frac{(x'-x'_0)^2}{a^2} + \frac{(y'-y'_0)^2}{b^2} = 1$$

We get: $$x'_0 = \frac{-D'}{2A'}$$ $$y'_0 = \frac{-E'}{2C'}$$

$$a^2 = \frac{-4F'A'C'+C'D'^2+A'E'^2}{4A'^2C'}$$ $$b^2 = \frac{-4F'A'C'+C'D'^2+A'E'^2}{4A'C'^2}$$

The coordinates of the centerpoint are found by rotating back about angle $\theta$

$x_0 = x'_0 \cos{\theta} - y'_0 \sin{\theta}$
$y_0 = x'_0 \sin{\theta} + y'_0 \cos{\theta}$

Cheers!

Answer 2

The equation that you give is the equation of a general conic. Some of which are ellipses, some hyperbolae, some parabolae, and other degenerate conics, e.g. $xy=0$, $x^2=0$ or $x^2+y^2=0$.

The non-degenerate cases are distinguished by the way the conics interact with the line at infinity. We have:

1. If $B^2-4AC < 0$ then we have an ellipse; the conic misses the line at infinity.
2. If $B^2-4AC = 0$ then we have a parabola; the conic is tangent to the line at infinity.
3. If $B^2-4AC > 0$ then we have a hyperbola; the conic crosses the line at infinity twice.

The centre of a conic is foung by solving the equations $\partial f/\partial x = \partial f /\partial y = 0$ where $f(x,y)$ is the equation you gave. In this case, assuming $B^2-4AC \neq 0$, we have the centre $(p,q)$ as:

$$(p,q) = \left(\frac{2CD-BE}{B^2-4AC},\frac{2AE-DB}{B^2-4AC}\right) . $$

As for the rotation, assume you have either an ellipse or a hyperbola. You need to complete the square on the $x^2$ and $x$ terms, as well as the $y^2$ and $y$ terms. This is equivalent to translating the conic so that its centre is at the origin. You can then re-label $(x-p)$ as $X$ and $(y-q)$ as $Y$ and divide through by a constant to give yourself a non-degenerate quadratic form, something like $aX^2+bXY + cY^2=1$ where $a$, $b$ and $c$ are real numbers. You then look at the matrix of the quadratic form:

$$Q = \left(\begin{array}{cc} a & \frac{1}{2}b \\ \frac{1}{2}b & c \end{array}\right) . $$

The eigenvectors of $Q$ give you the axes of the conic. In order to rotate the matrix, you need to find an orthogonal change of basis matrix which diagonalises $Q$. Finally, you will end up with $\alpha X^2+\beta Y^2=1$.

EXAMPLE

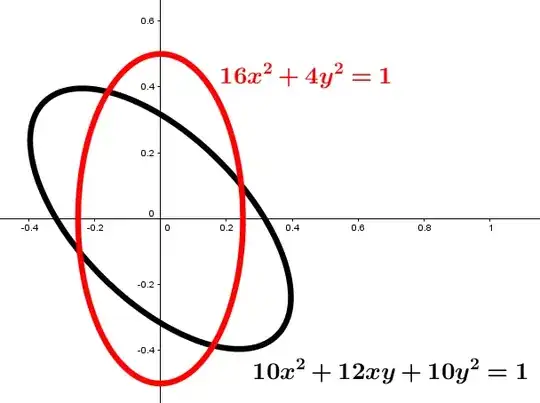
Take the example $10x^2+12xy+10y^2=1$. The quadratic form on the left has matrix $$M := \left(\begin{array}{cc} 10 & 6 \\ 6 & 10 \end{array}\right)$$ The eigenvectors of $M$ are $(1,1)^{\top}$ and $(1,-1)^{\top}$ with corresponding eigenvalues of $16$ and $4$ respectively. That gives $(1/\sqrt 2,1/\sqrt 2)^{\top}$ and $(1/\sqrt 2, -1/\sqrt 2)^{\top}$ as an orthogonal basis, i.e. unit length and perpendicular. Changing to this basis will diagonalise the quadratic form. (The change of basis will be a rotation.) If $$V:=\left(\begin{array}{cc} 1/\sqrt 2 & 1/\sqrt 2 \\ 1/\sqrt 2 & -1/\sqrt 2\end{array}\right) \ \ \ \mbox{and} \ \ \ D:=\left(\begin{array}{cc} 16 & 0 \\ 0 & 4 \end{array}\right)$$ then $MV=VD$. The matrix $V$ is orthogonal, and so $V^{-1}=V^{\top}$ meaning that $D=V^{-1}MV=V^{\top}MV$. If $x = {x\choose y}$ then \begin{eqnarray*} x^{\top}D x &=& x^{\top}V^{\top}MV x \\ \\ &=& (V x)^{\top}M(V x) \end{eqnarray*} A change of coordinates $x \mapsto Vx$ will diagonalise the quadratic form. If we put \begin{eqnarray*} x &=& \frac{1}{\sqrt 2}\,X + \frac{1}{\sqrt 2}\,Y \\ \\ y &=& \frac{1}{\sqrt 2}\, X - \frac{1}{\sqrt 2}\, Y \end{eqnarray*} then $10x^2+12xy+10y^2 \leadsto 16X^2 + 4Y^2$. Meaning that the locus $10x^2+12xy+10y^2=1$ can be rotated to the locus $16x^2+4y^2=1$, which is an ellipse crossing the $x$-axis at $\pm \frac{1}{4}$, and the $y$-axis at $\pm \frac{1}{2}$.

Answer 3

$Ax^2+Bxy+Cy^2+Dx + Ey +F=0 \hspace{2 mm} .. (1)$ represents a general equation for conic. It includes a pair of straight line, circles, ellipse, parabola, and hyperbola. For this general equation to be an ellipse, we have certain criteria.

Suppose this is an ellipse centered at some point $(x_0, y_0)$. Our usual ellipse centered at this point is $$\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 \hspace{ 2 cm } (2)$$

Note that this term does not have $xy$ term. This term appears due to rotation. So let's us counter rotate it such that $xy$ term vanishes. We let $x = X \cos \theta + Y \sin \theta$ and $y = - X \sin \theta + Y \cos \theta $, we plug this into $(1)$ and equate the coefficient of $xy$ to $0$ since we assume that by rotation $(xy)$ vanishes. From here, we can calculate $\theta $. If it's an ellipse then we are be able to reduce the remnant of $(1)$ into the form $(2)$. Hence we find the center.

Answer 4

For the vice versa part of the question: the parameterization for the ellipse centered at the origin and with semi major axis equal to $a$ (parallel to the frame of reference) and semi minor axis equal to $b$ is

$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}\qquad\varphi\in[0,2\pi)$$

If I rotate the ellipse of the angle $\theta$ with the rotation matrix $R=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}$ I will get:

$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\cdot\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}$$

If I translate the center from $(0,0)$ to $(x_c,y_c)$ I will get:

$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\cdot\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}+\begin{pmatrix}x_c\\y_c\end{pmatrix}$$

Now I would like to isolate $\cos\varphi$ and $\sin\varphi$, then square them and finally get the quadratic form.

$$\begin{pmatrix}x-x_c\\y-y_c\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\cdot\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}$$

Since $R$ is a rotation matrix, it holds $R^{-1}=R^T$ and so I can multiply both sides by $R^T$:

$$\begin{pmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{pmatrix}\cdot\begin{pmatrix}x-x_c\\y-y_c\end{pmatrix}=\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}$$

Now I do the matrix vector product:

$$\cos(\theta)(x-x_c)+\sin(\theta)(y-y_c)=a\cos\varphi$$

$$-\sin(\theta)(x-x_c)+\cos(\theta)(y-y_c)=b\sin\varphi$$

and I isolate $\cos\varphi$ and $\sin\varphi$:

$$\frac{\cos(\theta)(x-x_c)+\sin(\theta)(y-y_c)}{a}=\cos\varphi$$

$$\frac{-\sin(\theta)(x-x_c)+\cos(\theta)(y-y_c)}{b}=\sin\varphi$$

Now, since $\cos^2\varphi+\sin^2\varphi=1$, I get

$$\left(\frac{\cos(\theta)(x-x_c)+\sin(\theta)(y-y_c)}{a}\right)^2+ \left(\frac{\cos(\theta)(y-y_c)-\sin(\theta)(x-x_c)}{b}\right)^2=1$$

I will now use sympy to extract the coefficients $A$, $B$, $C$, $D$, $E$, $F$ of the quadratic form $$Ax^2 + By^2 + Cxy + Dx + Ey + F = 0$$

from sympy import *
theta,x_c,y_c,a,b,x,y=symbols('theta x_c y_c a b x y')
exp_1=((cos(theta)*(x-x_c)+sin(theta)*(y-y_c))/a)**2+((cos(theta)*(y-y_c)-sin(theta)*(x-x_c))/b)**2-1
exp_2=expand(exp_1)
P=poly(exp_2,x,y)
A,B,C,D,E,F=symbols('A B C D E F')
A_=P.coeff_monomial(x**2)
B_=P.coeff_monomial(y**2)
C_=P.coeff_monomial(x*y)
D_=P.coeff_monomial(x)
E_=P.coeff_monomial(y)
F_=P.coeff_monomial(1)
print(latex(relational.Eq(A, A_)))
print(latex(relational.Eq(B, B_)))
print(latex(relational.Eq(C, C_)))
print(latex(relational.Eq(D, D_)))
print(latex(relational.Eq(E, E_)))
print(latex(relational.Eq(F, F_)))

$$A = \frac{1}{b^{2}} \sin^{2}{\left (\theta \right )} + \frac{1}{a^{2}} \cos^{2}{\left (\theta \right )}$$ $$B = \frac{1}{b^{2}} \cos^{2}{\left (\theta \right )} + \frac{1}{a^{2}} \sin^{2}{\left (\theta \right )}$$ $$C = - \frac{2}{b^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )} + \frac{2}{a^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )}$$ $$D = - \frac{2 x_{c}}{b^{2}} \sin^{2}{\left (\theta \right )} + \frac{2 y_{c}}{b^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )} - \frac{2 x_{c}}{a^{2}} \cos^{2}{\left (\theta \right )} - \frac{2 y_{c}}{a^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )}$$ $$E = \frac{2 x_{c}}{b^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )} - \frac{2 y_{c}}{b^{2}} \cos^{2}{\left (\theta \right )} - \frac{2 x_{c}}{a^{2}} \sin{\left (\theta \right )} \cos{\left (\theta \right )} - \frac{2 y_{c}}{a^{2}} \sin^{2}{\left (\theta \right )}$$ $$F = -1 + \frac{x_{c}^{2}}{b^{2}} \sin^{2}{\left (\theta \right )} - \frac{2 x_{c}}{b^{2}} y_{c} \sin{\left (\theta \right )} \cos{\left (\theta \right )} + \frac{y_{c}^{2}}{b^{2}} \cos^{2}{\left (\theta \right )} + \frac{x_{c}^{2}}{a^{2}} \cos^{2}{\left (\theta \right )} + \frac{2 x_{c}}{a^{2}} y_{c} \sin{\left (\theta \right )} \cos{\left (\theta \right )} + \frac{y_{c}^{2}}{a^{2}} \sin^{2}{\left (\theta \right )}$$

Inspired by Compute center, axes and rotation from equation of ellipse

See also https://en.wikipedia.org/wiki/Ellipse#General_ellipse