10

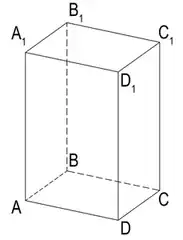
In a math textbook for primary school, there's a picture like the one below. They explain which of the line segments are perpendicular and which are parallel to AD.

a cuboid

There's also a note stating that A1B1, D1C1, BB1 and CC1 are neither parallel nor perpendicular to AD.

I was wondering about that statement, because I learned that those four are perpendicular to AD. So I wrote to the book publisher asking about that. They replied that actually there are two conventions for this situation and they choose "not perpendicular" which, according to them, is more popular.

Is there really no consensus on that?

Edit:
I found another question here, related to a mathematical consensus: Is $0$ a natural number? and I'd accept an answer referring to some resources and clarifying whether the consensus exists or not.

TazGPL
  • 203
  • 3
    Under the usual convention, two lines can only be perpendicular if they are in the same plane. Any two non-intersecting, non-parallel lines are necessarily skew. – Ben Grossmann May 08 '17 at 18:48
  • 3
    @Omnomnomnom Using the definition that "two lines are perpendicular if they intersect at a right angle" yes, skew lines cannot be pependicular. However, I can also see OP's confusion (and +1'd the question). For example Wikipedia says "A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron". But then the Orthocentric tetrahedron is defined as "a tetrahedron where all three pairs of opposite edges are perpendicular". – dxiv May 08 '17 at 18:59
  • An interesting fact is that if you have two lines which intersect, then there exists a plane containing both of them. – Michael Burr May 08 '17 at 19:05
  • Interesting. Did the book give a formal definition of either parallel or perpendicular? If parallel means, naively that "they never intersect" (a poor definition) then skew lines are parallel. If the definition of perp is something like, there exist points on each line so that for any two points on one line that are equidistant from one point they are equivalent distance from the other, skew are perp. But if it's intersect at right angles, they aren't. – fleablood May 08 '17 at 19:11
  • 1
    I would rather say that the vectors associated to the line segments are orthogonal (or perpendicular). – MasB May 08 '17 at 20:24
  • 1
    Related: "What do you call 'perpendicular but skew' lines?" Also: "Must perpendicular (resp. orthogonal) lines meet?" – Blue May 09 '17 at 01:28
  • Thanks for your comments and very interesting articles shared. I kept reading and found another question here related to a mathematical consensus (updating the question). @fleablood No, they didn't give a formal definition, just that statement. – TazGPL May 09 '17 at 21:32

2 Answers2

1

According to Wikipedia, "skew lines are two lines that do not intersect and are not parallel."

Two sentences later it wrote "Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions."

Therefore, skew lines (at least if you trust the Wikipedia definition) cannot be perpendicular.

KingLogic
  • 1,441
-1

I think, Since, A1B1 and AD are not on the same plane, we can't say they are parallel or perpendicular. But your title asks whether skew lines can be perpendicular or not? - I say, Yes, but if two lines are originally perpendicular and you skew them horizontally or vertically (or both) they are will not remain perpendicular.

Sushant
  • 1